Kräfte (2): Kräfte zerlegen 01.08.2009, 09:49
Man kann eine gegebene Kraft in zwei (oder mehr) andere Teilkräfte zerlegen. Zusammen haben diese dieselbe Wirkung wie die unzerlegte Kraft. Mit Übungsbeispielen aus der Technik.
2. Ausbildungsjahr
Kräfte (2)
Im Beitrag Kräfte (1) haben wir beschrieben, wie man Kräfte darstellt und sie zusammensetzt. Mit der Vermutung, dass unter 10 Kräfteaufgaben höchstens eine sich mit dem Zusammensetzen von Kräften beschäftigt, liegt man sicher nicht falsch. Wesentlich häufiger kommt die Kräftezerlegung vor.
b) Kräfte zerlegen
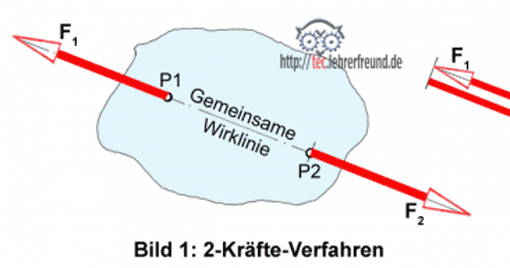
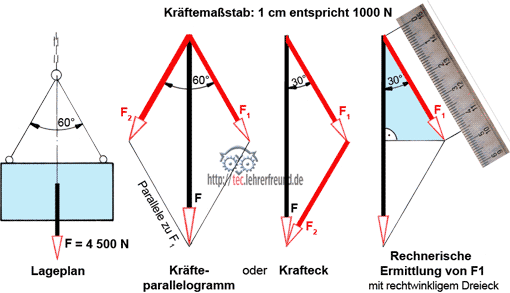
Man kann eine gegebene Kraft in zwei (oder mehr) andere Teilkräfte zerlegen. Diese haben dieselbe Wirkung wie die unzerlegte Kraft. Das heißt aber nicht, dass die Teilkräfte F1 und F2 (Bild) zusammmengenommen gleich groß sind wie F, denn es handelt sich um eine so genannte geometrische Addition.
Ein Fall für das Zerlegen einer Kraft wäre beispielsweise die an Seilen aufgehängte Last.
Beispiel 1
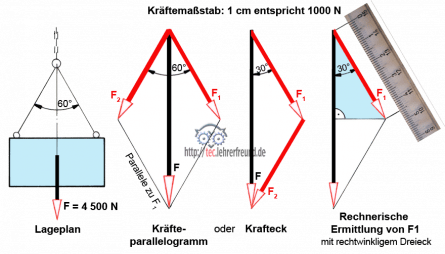
Angehängte Last: Wie ermittelt man die Seilzugkräfte?
Bei der Zerlegung einer Kraft F geht man vor wie folgt:
- Kräfteparallogramm
1. Gegebene Kraft F im zuvor festgelegten KM zeichnen
2. Wirkungslinie der ersten Teilkraft durch den Anfang von F ziehen
3. Wirkungslinie der zweiten Teilkraft durch den Anfang von F ziehen
4. Durch die Pfeilspitze von F Parallelen zu den Wirkungslinien von F1 und F2 legen
5. Die Teilkräfte ergeben sich durch die so erhaltenen Schnittpunkte.
- Krafteck
1. Gegebene Kraft F im zuvor festgelegten KM zeichnen
2. Wirkungslinie der ersten Teilkraft durch den Anfang von F ziehen
3. Wirkungslinie der zweiten Teilkraft durch die Pfeilspitze von F ziehen
4. Am Schnittpunkt der Wirkungslinien endet F1
5. Die Teilkraft F2 endet am Pfeil von F.
Die Seilzugkräfte lassen sich auch rechnerisch ermitteln. Dazu muss man das geeignete rechtwinkelige Dreieck finden:
cos α = AK : H –> H = AK : cos AK : cos α = AK : cos 30° = 4500 N : 2 : 0,866 –> F1 = 2 598 N
(AK = Ankathete; H = Hypotenuse)
Beispiel 2
Häufig angewendet wird die Zerlegung einer Kraft in zwei senkrecht aufeinander stehende Einzelkräfte.
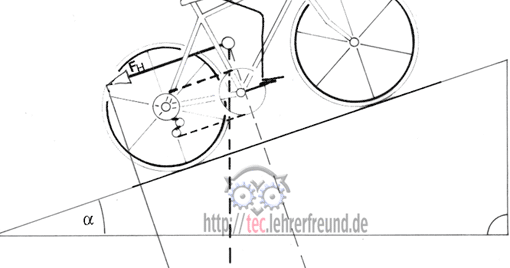
Das Eigengewicht FG des Muldenkippers sitzt im Schwerpunkt des Fahrzeugs und zieht, wie jedes Gewicht, senkrecht nach unten. FG wirkt sich so aus, dass der Muldenkipper auf der Schiefen Ebene rückwärts fahren möchte. Außerdem drückt das Fahrzeug mit einer bestimmten Kraft auf die Fahrbahndecke; diese ist kleiner als FG. Die abwärts ziehende Kraft ist die Hangabtriebskraft FH, die auf den Boden drückende Kraft die Normalkraft FN. Beide entstehen aus der Gewichtskraft FG. Dabei ist zu beachten, dass die (geometrische) Summe FN + FG größer ist als FG.
Die folgenden Skizzen zeigen die Konstruktion des Kräfteparallelogramms.
FH und FG sind je nach Steigungswinkel α unterschiedlich groß: Je steiler die Schiefe Ebene wird, desto stärker treibt es den Wagen auf seiner Bahn nach unten (FH). Gleichzeitig wird die Fahrbahn weniger belastet (FN).
Übungen
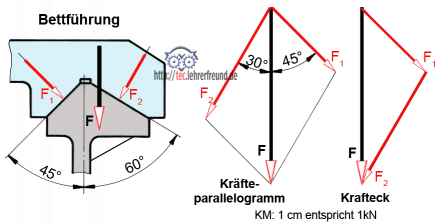
Prismenführung
Drehmaschine: Der Werkzeugschlitten (blau) drückt mit F = 4,2 kN auf die Bettwange. Ermitteln Sie zeichnerisch F1 und F2.
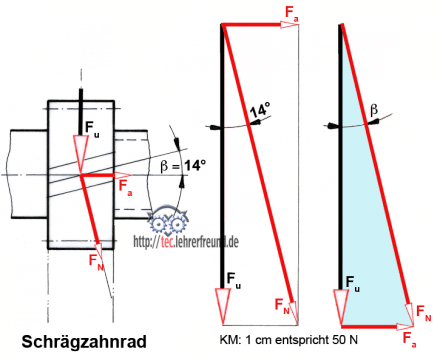
Zahndruck beim schrägverzahnten Stirnrad
Wegen ihres leisen Laufs werden in Getrieben häufig schrägverzahnte Stirnräder verwendet. Sie erzeugen allerdings eine axiale Kraftkomponente Fa.
Umfangskraft Fu = 630 N, Schrägungswinkel β = 14°. Ermitteln Sie zeichnerisch und rechnerisch FN und Fa.
Berechnung der Kräfte FN und Fa
cos β = Fu : FN –> FN = Fu : cos β
= 420 N : 0,9702 =
FN = 432,9 N
sin β = Fa : FN –> Fa = FN ⋅ sin β =
Fa = 101,6 N
__________