Drehmomente (2): Kräfte, Druck, Festigkeit 25.08.2009, 14:42

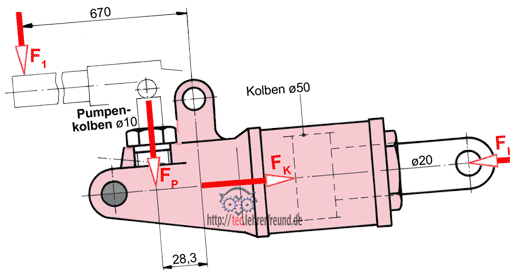
Der Wagenheber ist für eine Hublast bis 2 Tonnen ausgelegt. In den Aufgaben gehen wir davon aus, dass diese Höchstlast mittig auf dem Sattel sitzt. Themen: Kräfte, Drehmomente, Flüssigkeitsdruck und Festigkeitsberechnung.

2., 3. und 4. Ausbildungsjahr

Wagenheber

Der Wagenheber (siehe Drehmomente (1)) ist für eine Hublast bis 2 Tonnen (= 2 000 daN = 20 000 N) ausgelegt. In den Aufgaben gehen wir davon aus, dass diese Höchstlast auf den Sattel aufgesetzt ist. Drehpunkt des Hubarms ist die grau angelegte Achse. 

Die folgenden Übungen befassen sich mit den Themen Kräfte, Drehmomente, Flüssigkeitsdruck und Festigkeitsberechnung.

Aufgabe 1
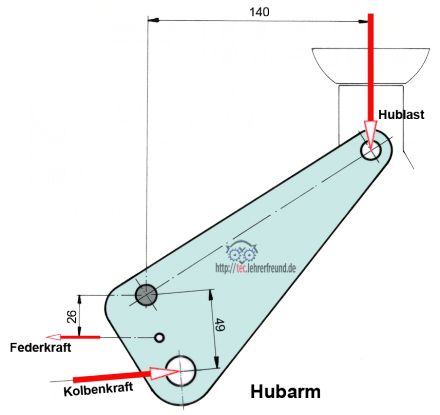
Berechnen Sie die Kolbenkraft F_K, wenn die Rückzugfeder mit F_F = 1 500 N zieht.

Lösung:
F_L und F_F erzeugen rechtsdrehende Momente, F_K erzeugt ein linksdrehendes Moment.
Summe der M_L = Summe der M_R, anders geschrieben: Σ M_L = Σ M_R 
F_K · l_K – F_F · l_F = F_L · l_L
F_K = (F_L · l_L + F_F · l_F) : l_K
F_K =  (20 000 N · 140 mm + 1500 N · 26 mm) : 49 mm
F_K = 57 938,8 N = 5 739 daN

Aufgabe 2

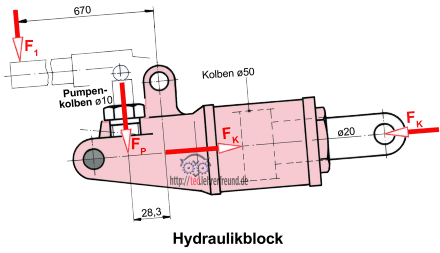
a) F_K wird vom Kolben ø50 aufgebracht. Wie hoch ist der Öldruck p?
b) Die Kraftübersetzung i_K im Hydraulikblock entspricht dem Verhältnis der Kolbenflächen A_K : A_P . Wie groß ist i_K?
c) Mit welcher Kraft F_P muss der Pumpenkolben gedrückt werden?
d) Wie groß ist dabei die Handkraft F₁?

Lösungen:
 a) p = F_K : A = F_K : (5 cm)² · π : 4 = 5 635 daN : 25cm² · π : 4 = 287 daN/cm² =
p = 287 bar

b) i_K = A_K : A_P = d_K² ⋅ π : 4  :  d_P² ⋅ π : 4 = d_K² :  d_P² = (5 cm)² : (1 cm)² =
    i_K = 25 : 1
c) F_P = p · A_P = 287 daN/cm² · (1cm)²  · π : 4 = 225,4 daN = 2254 N
d) F₁  ·  l₁ = F_P  ·  l_P  –> F₁ = F_P  ·  l_P : l₁ = 2254 N · 30 mm : 670 mm =
F1 = 100,9 N

Aufgabe 3
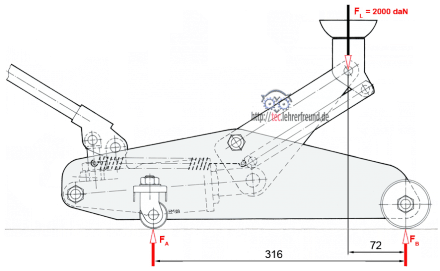
Berechnen Sie für die gezeichnete Stellung die auf die Radlager wirkenden Stützkräfte F_A und F_B. Das Eigengewicht des Wagenhebers soll dabei unberücksichtigt bleiben.

Lösung:
Drehpunkt im Lager A gewählt.
F_L · (316 – 72) mm = F_B · 316 mm –> F_B = 2 000 daN · 244 mm : 316 mm =
F_B = 1 544,3 daN
F_A = 2 000 daN - 1 544,3 daN =
F_A = 455,7 daN

Aufgabe 4
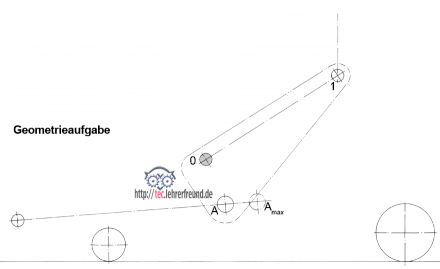
Geometrieaufgabe: Die Kolbenstange fährt bis Punkt A_max aus und schwenkt dabei den Hubarm nach oben.

a) Zeichnen Sie den Kreis, auf dem sich A_max bei Betätigung des Hubarms bewegt.
b) Zeichnen Sie den Kreis, auf dem sich die Hubarmbohrung A bewegt.
c) Wo steht dann A_max?
d) Wo ist bei Erreichen von c) die Bohrung 1 des Hubarms?

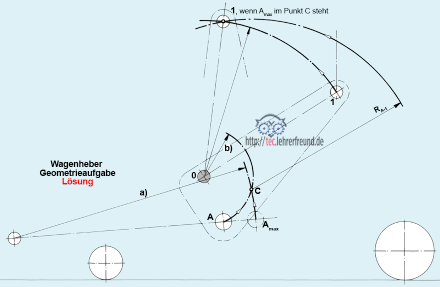
Aufgabe 4 Lösung: siehe Zeichnung

Aufgabe 5
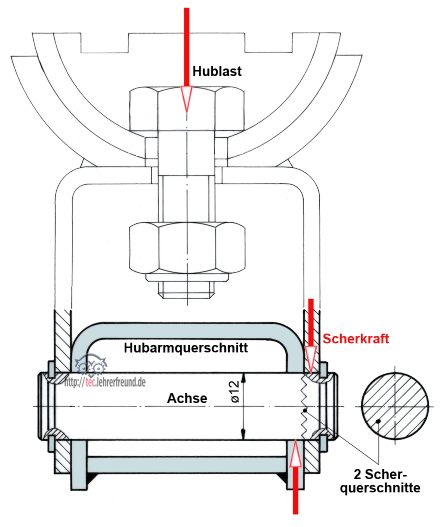
Bei voller Belastung des Wagenhebers ist bei einer Reihe von Bauelementen eine ausreichende Festigkeit gefragt. Wir betrachten z. B. den äußeren Bolzen des Hubarms, der vom U-förmigen Tragsattel auf Abscherung beansprucht wird. Hier spricht man von einer »zweischnittigen« Verbindung, weil sich die Hublast F_L auf zwei Scherquerschnitte verteilt.

Beanspruchung auf Abscherung
Bei der Abscherbeanspruchung entstehen Spannungen in einer Querschnittsfläche, die parallel zur angreifenden Kraft liegt. Als Querschnittsfläche S gilt die Summe aller Scherflächen, die im Falle des Trennens Bruchflächen ergeben. Die Scherspannung ist von anderer - man kann sagen, von gefährlicherer - Art als die Zugspannung, weshalb sie nicht das Symbol σ (sigma), sondern τ (tau) erhielt.

Bezeichnungen:

F = F_L  Scherkraft (in N)
S  Querschnittsfläche (in mm²)
τ _{a zul} (tau) zulässige Scherspannung (N/mm²)
τ_aB Scherfestigkeit (N/mm²)
ν (nü) Sicherheitszahl

In die Festigkeitsberechnungen ist die durch Versuche ermittelte oder Tabellen entnommene Scherfestigkeit τ_aB einzusetzen; aus ihr lässt sich mit Hilfe einer Sicherheitszahl ν die zulässige Scherspannung τ _{a zul} ermitteln. Für Stahl gilt, wenn τ_aB nicht bekannt ist, näherungsweise auch τ_aB = 0,8 • R_m.

Aufgaben:

a) Die Achse aus SR275JR wird auf Abscherung beansprucht. Mit welcher Scherkraft F (hier F_L) darf sie belastet werden?
Scherfestigkeit τ_aB = 340 N/mm²; Sicherheitszahl ν = 1,4
b) Wie hoch ist die Flächenpressung bei einer Blechdicke s = 3 mm? Bei mittelhoch belastbaren Stahlsorten wie SR275JR soll p = 50 N/mm² nicht überschreiten. Der Wert hängt auch von der Genauigkeit ab, mit der die Teile ineinander gefügt sind. Sitzt der Bolzen mit großem Spiel im Lagerblech, was bei unserem einfachen Wagenheber angenommen werden darf, dann bewegt sich die Auflagefläche auf eine kritische, nur bedingt belastbare Punktauflage zu.

Lösungen: 

a) τ _{a zul} = τ_aB : ν = 340 N/mm²: 1,4 = 242,9 N/mm²
 

F_L = 2 • S • τ_{a zul}  = 2 • d² • π :4 • τ_{a zul}

F_L = 2 • (12mm)² • π :4 •  242,9 N/mm²

F_L = 54 943 N = 5 494 daN ≙ 5 Tonnen. Abscherung ist demnach keine Gefahr für die Achse, weil sie nur mit max. 2 t beansprucht wird.

b) p = F_L/2 : A = F_L/2 : (d ⋅ s) = 10 000 N : 12 mm : 3 mm =
    p = 278 N/mm²

Dieser Wert, der auf einer Belastung von 2 Tonnen beruht, überschreitet also die zulässige Flächenpressung um das annähernd Sechsfache!