Kontrollmessung mit Messwalzen 18.09.2017, 06:52
Wie misst man den Abstand zwischen schrägen Flächen genau, wenn man keine ausgeprägten Messflächen zur Verfügung hat? Die Lösung sind Messwalzen.
Kontrollmaßbestimmungen mit Hilfe von Messwalzen
Aufgabe: Wir sollen
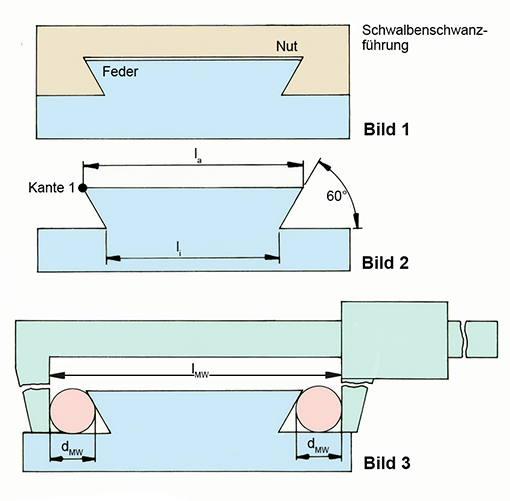
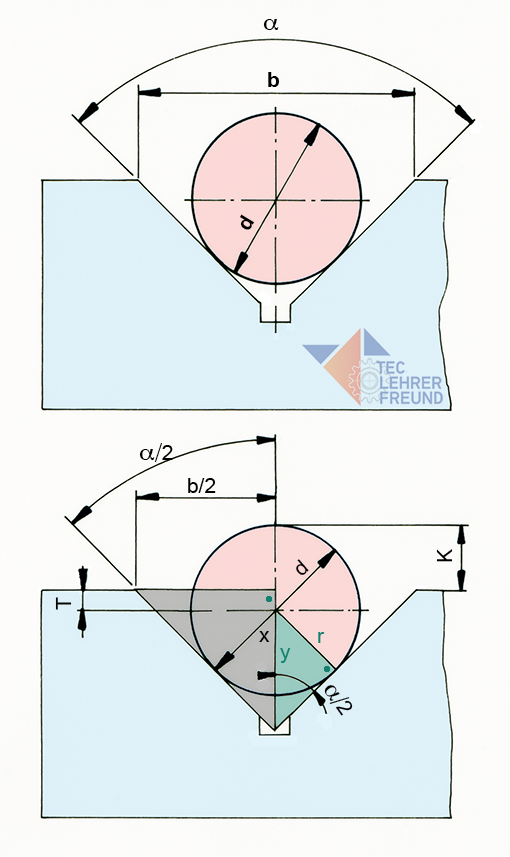
a) den Abstand der Bahnen einer Schwalbenschwanzführung messen (Bilder 1 und 2),
b) den Rillendurchmesser einer Riemenscheibe messen.
Wie misst man solche Abstände genau, wenn man keine ausgeprägten Messflächen zur Verfügung hat?
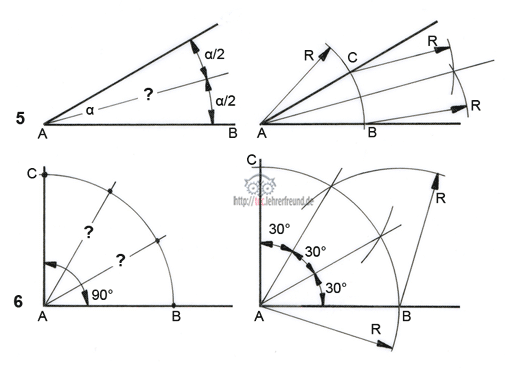
Bild 3: Das Prüfen schräger Flächen in der Technik ist meist nicht ohne das Hilfsmittel des Messzylinders möglich. Je nach geometrischer Form ermittelt man die Kontrollmaße mit einer jeweils eigenen Berechnung. Dem Schüler stellt sich dabei die Frage: Welches rechtwinklige Dreieck bietet sich für meine Rechnung an? Dabei helfen folgende Beobachtungen (Bild 4):
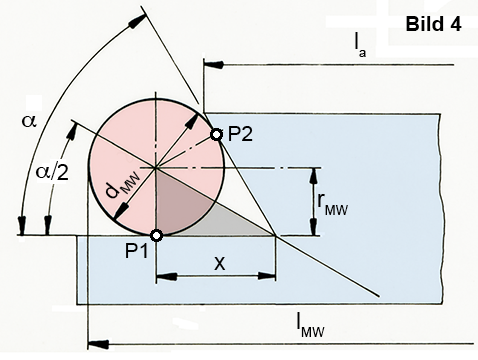
– Der Messzylinder liegt immer an zwei Flächen an: P1 und P2.
– Der Mittelpunkt des Messzylinders dMW ist eine Ecke des rechtwinkligen Hilfsdreiecks. Dieses wird durch den Schnittpunkt der beiden Flächen, den Mittelpunkt des Zylinders und einen Berührpunkt gebildet. Darin sind bekannt:
– der Radius des Messzylinders rMW,
– der Mittelpunkt des Messzylinders; er liegt auf der Winkelhalbierenden zwischen den Flächen.
Bei einer Schwalbenschwanzführung ist die Innenform (der Schlitten) die »Nut«, die Außenform die »Feder« (Bild 1).
Beispiel: Die Prüfung der Feder mit den Maßen li und la
Kann man davon ausgehen, dass die Messung der Maße li und la exakt ist? Nein, man kann es nicht. Dazu müsste die Kante 1 (Bild 2, und ihre gegenüber liegende Kante) messerscharf und ohne Grat sein. Auch müsste das Material gewährleisten, dass es vom Prüfzeug nicht eingedrückt wird. Weil beide Forderungen nicht zu erfüllen sind, misst man über Messwalzen das Maß lMW.
Bild 4: lMw = li + 2 • (x + rMW)
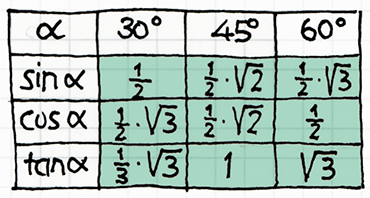
tan α/2 = rMW : x ––> x = rMw : tan α/2.
Bei den Maßen dMw = 16 mm, li = 210 mm und α = 60° ergibt sich:
x = 8 mm : 0,577 = 13,865 mm
lMw = 210 mm + 2 • (13,865 mm + 8 mm) =
lMW = 253,73 mm
Messzylinder im Prisma
Beim Ausmessen einer prismatischen Form (Bilder 5 und 6 unten) geht es darum, die Lage der Messwalze zur Oberfläche des Prismas (Maß T) zu ermitteln. Der Walzenradius r minus T ergibt das gesuchte Kontrollmaß K. Der Weg dorthin führt über zwei rechtwinklige Dreiecke, das linke mit der Kathete x, das rechte mit der Hypothenuse y (Bild 6).
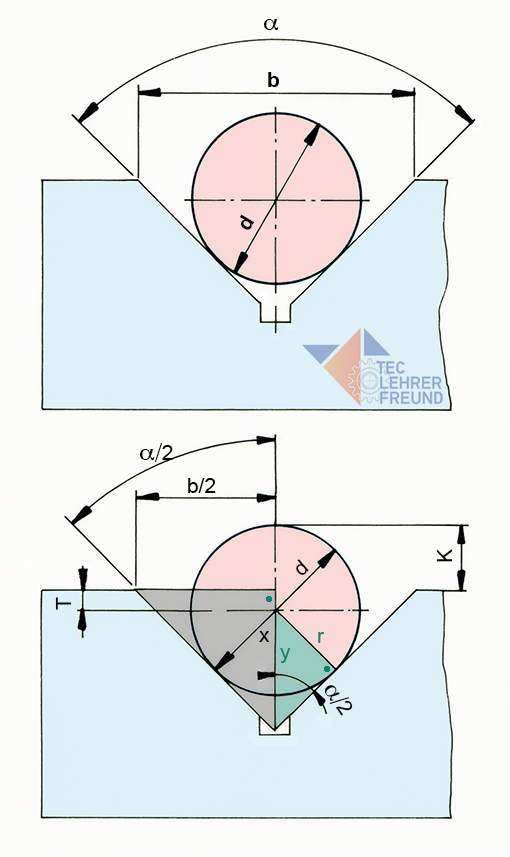
Bilder 5 (oben) und 6
Maße: a = 90°; b = 30 mm; d = 16 mm
K = r – T ––> x berechnen
a/2 = 45° ––> tan a/2 = b/2 : x ––> x = b/2 : tan 45°
x = 15 mm : 1,0 =
x = 15 mm
y berechnen:
sin a/2 = r : y ––> y = r : sin a/2 = 8 mm : 0,707
y = 11,315 mm
T = x – y = 15 mm – 11,315 mm =
T = 3,686 mm
K = r – T = 8 mm – 3,685 mm
K = 4,315 mm = Kontrollmaß