Kräfte an einer Stehleiter 29.12.2017, 07:08

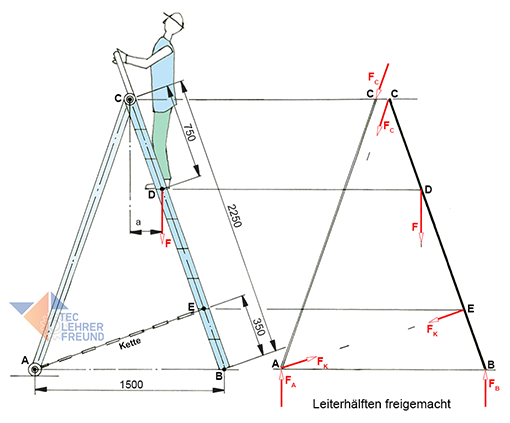
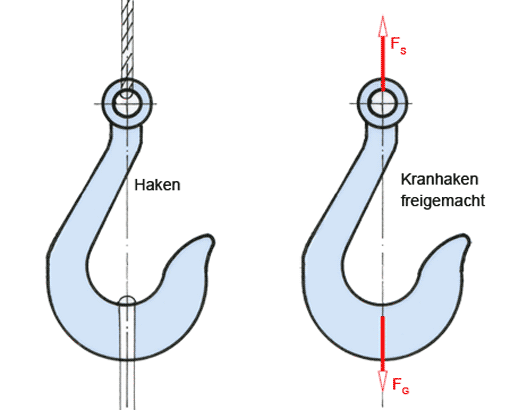
In dieser Statikaufgabe sollen die beiden Leiterhälften freigemacht und zeichnerisch die Stützkraft FB, die Bolzenkraft FC und die Kettenkraft FK bestimmt, sowie rechnerisch die Stützkräfte FA und FB ermittelt werden.

Bockleiter 

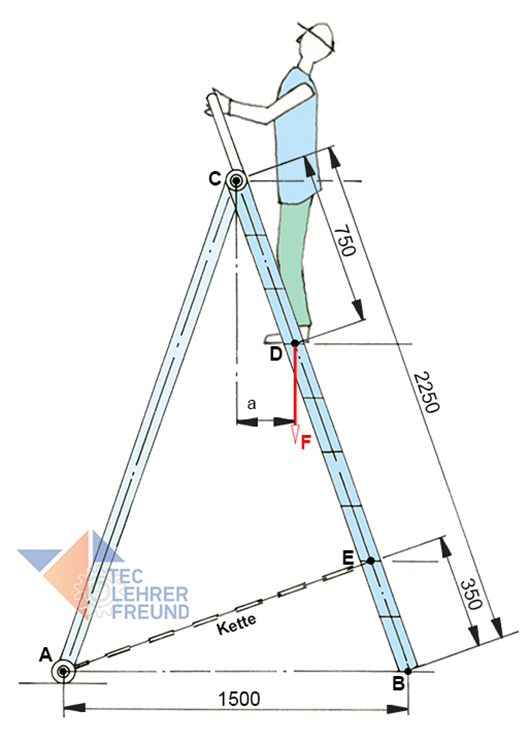
In der vorliegenden Aufgabe geht es um eine Stehleiter oder Bockleiter. Eine Kette am unteren Teil der Leiter verhindert, dass die Beine beim Besteigen auseinanderrutschen. Im Punkt C sitzt ein Gelenkbolzen.
In der Berechnung soll das Eigengewicht der Leiter unberücksichtigt bleiben. 

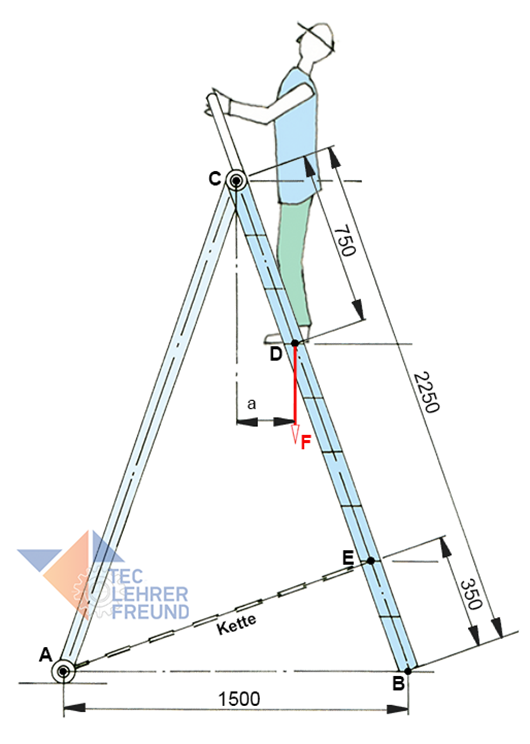
In der ersten Aufgabe sollen die beiden Leiterhälften freigemacht werden. Dabei stellt sich heraus, dass auf die rechte Leiterhälfte vier Kräfte wirken. Welche sind es? Gegeben ist die senkrecht nach unten wirkende Maximallast F mit 1 000 N.

Näheres dazu finden Sie im Beitrag  
https://www.lehrerfreund.de/technik/1s/kraefte-unbekannte-kraefte-zeicherisch-ermitteln-2/3780 

Aufgaben: 

1. Die beiden Leiterhälften freimachen.

2. Zeichnerisch die Stützkraft F_B, die Bolzenkraft F_C und die Kettenkraft F_K bestimmen.

3. Die Winkel α und β durch Herausmessen finden.

4. Rechnerisch die Stützkräfte F_A und F_B bestimmen.

Die in Aufgabe 2. gefundenen Ergebnisse sollen in 4. nicht verwendet werden. 

Lösungsvorschläge 

1. Wie macht man ein belastetes Bauteil frei? 
Wir betrachten die rechte Leiterhälfte. Diese denkt man sich von ihrem Kontakt mit der linken Leiterhälfte im Drehpunkt C und dem Boden befreit. Auch die auf einer Sprosse stehende Person wird entfernt und die Kette abgeschnitten. An ihrer Stelle zeichnet man diejenigen Kräfte ein, die jeweils wirksam werden können. Man muss sich also überlegen, welche Kraftwirkung die weggenommenen Umgebungsteile auf die rechte Leiterhälfte ausüben. 

Auf die linke Leiterhälfte wirken die Stützkraft F_A, die Kettenkraft F_K und die Bolzenkraft F_C.

Auf die rechte Leiterhälfte wirken vier Kräfte: die Stützkraft F_B, die Kettenkraft F_K, die Trittkraft F und die Bolzenkraft F_C.

2.  Zeichnerisch die Stützkraft F_B, die Bolzenkraft F_C und die Kettenkraft F_K bestimmen, herausmessen und über den Kräftemaßstab KM berechnen. 

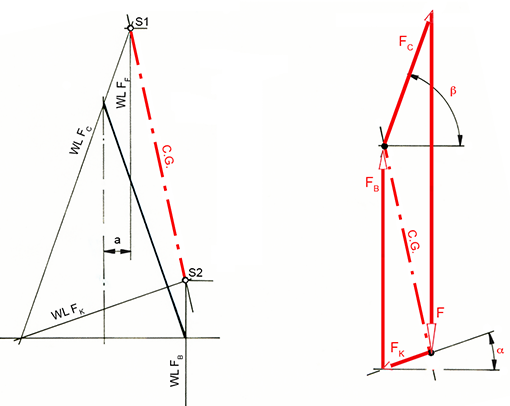
Diese Aufgabe lösen wir mit Hilfe der Culmannschen Geraden. Wir fassen hier kurz zusammen, was sie besagt und wie mit ihr gearbeitet wird. Sie hilft weiter, wenn man ein Gleichgewicht von vier nicht parallelen Kräften benötigt. Dabei geht man von der Überlegung aus, dass im System ein Gleichgewicht nur vorhanden ist, wenn die Resultierenden von je zwei Kräften auf derselben Wirklinie liegen und gegeneinander wirken. 

Lösungsweg:
– den Lageplan zeichnen und dort die Wirklinien je zweier Kräfte zum Schnitt bringen.
– Punkt S1 ist der Schnittpunkt der Wirklinien von F_C und F. F_B und F_K schneiden sich im Schnittpunkt S2.
– Damit ist die durch S1 und S2 gehende Culmannsche Gerade gefunden, und der Kräfteplan kann gezeichnet werden (Bild rechts). 

Längenmaßstab: LM 1 cm ≜ 200 mm 

Kräftemaßstab: KM 1 cm ≜ 300 N 

F_B = 670 N

F_C = 400 N

F_K = 150 N

3. Die Winkel α und β durch Herausmessen finden 

Für α wird gemessen 19°;  für β wird gemessen 70° 

4. Rechnerisch die Stützkräfte F_A und F_B bestimmen 

Wir betrachten die Gesamtleiter, auf die die äußeren Kräfte F_A, F_B und F wirken.

ΣM_A = 0 = F_B • 750 – F • (750 – a)

     Abstand a aus proportionalen Dreiecke berechnet: a : 750 mm = 750 mm : 2250 mm ––>
     a = 250 mm 

F_B = 1000 N • 500 mm  / 750 mm 

F_B = 666,7 N

ΣF_y = 0 = FA – F + F_B ––> 

F_A = F –  F_B = 1000 N – 666,7 N 

F_A = 333,3 N