Bruchrechnen (1) 10.10.2017, 06:01
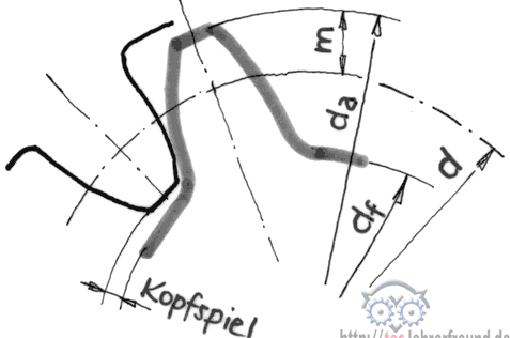
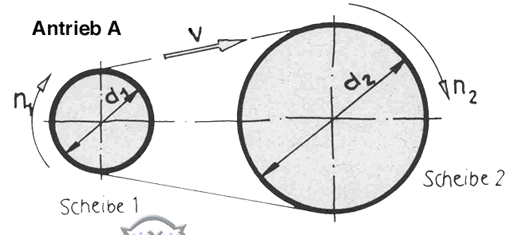
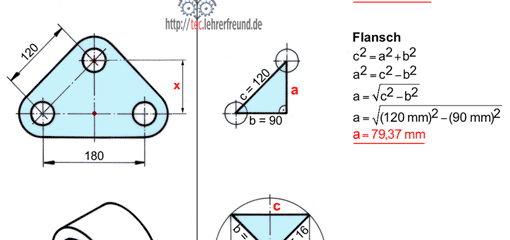
Wenn man ein Ganzes in gleich große Teile zerlegt, umschüttet usw., entstehen Bruchteile des Ganzen. In der technischen Mathematik kommen sie oft vor, wenn man Kegel, Zahnräder, Riementriebe oder Übersetzungsverhältnisse berechnet.
Bruchrechnen
Wenn man ein Ganzes (ein Grundstück, einen Eisenstab, einen Liter Wasser usw.) in gleich große Teile zerlegt, umschüttet usw., entstehen Bruchteile des Ganzen. In der technischen Mathematik kommen sie vor, wenn man beispielsweise Kegel, Zahnräder, Riementriebe oder Übersetzungsverhältnisse berechnet.
Beispiel:
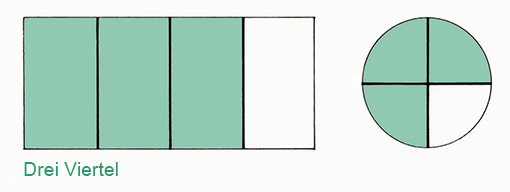
Wir teilen eine Rechteckscheibe in gleich große Viertelabschnitte auf (Bild 1). Ein Viertel ist grün gezeichnet. Rechts daneben ist ein Viertel in Kreisdarstellung gezeichnet.
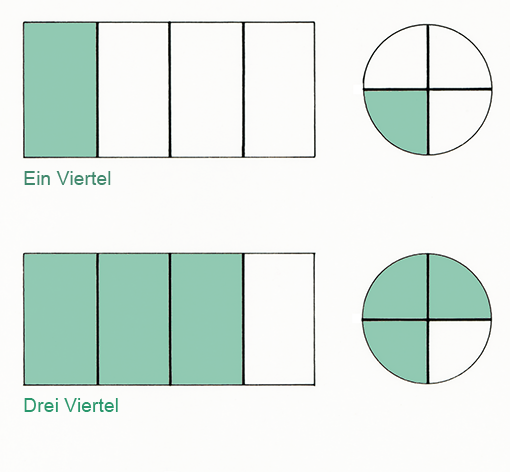
Oben: Bilder 1 und 2
Dabei müssen wir uns an die spezielle Schreib- und Sprechweise gewöhnen: Ein Viertel, zwei Viertel, drei Viertel usw., echter Bruch, unechter Bruch usw.
Als Bruchterm schreibt man Viertel 1/4, 2/4, 3/4 usw. Der Schrägstrich bedeutet geteilt (dividiert):
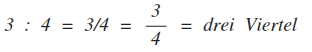
(In der Mathematik bezeichnet der Begriff Term einen sinnvollen Ausdruck, der Zahlen, Variable, Symbole (für mathematische Verknüpfungen) und Klammern enthalten kann.)
Zähler und Nenner:
In
ist 3 der Zähler, 4 der Nenner.
Brucharten
In 1/4 ist Zähler < Nenner. Dies ergibt einen Wert < 1 (hier 0,25). Wir sprechen von einem echten Bruch.
In 5/4 ist Zähler > Nenner. Dies ergibt einen Wert > 1 (hier 1,25). Wir sprechen von einem unechten Bruch.
1 1/4 = Eineinviertel = eine ganze Zahl und ein echter Bruch. Der Wert ist > 1. Wir sprechen von einer gemischten Zahl.
0,20 hat ein Dezimalkomma; sein Wert ist < 1. 0,20 wird deswegen auch als Dezimalbruch bezeichnet·.
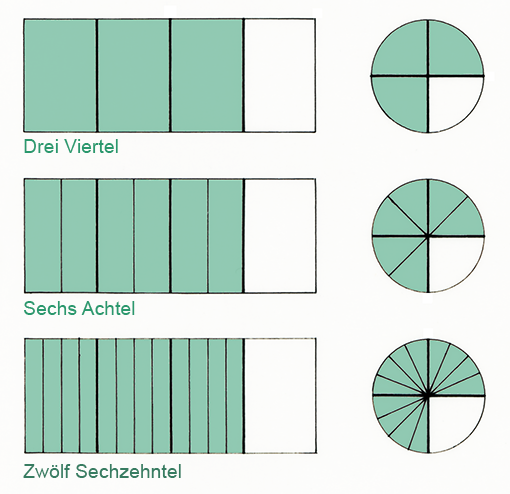
Bild 3
Bild 3 zeigt, dass unterschiedliche Brüche den gleichen Wert haben können. Die Fächen sind durch Erweitern entstanden. Man kann auch kürzen, einen echten Bruch in einen Dezimalbruch umwandeln, oder, umgekehrt, einen Dezimalbruch in einen echten Bruch umwandeln.
Vorsicht ist bei Summen und Differenzen geboten.
Rechenregeln
Brüche erweitern: Zähler und Nenner werden mit demselben Faktor multipliziert.
Beispiel 3/4, Faktor 5: 3 · 5 / 4 · 5 = 15/20
Mit Buchstaben: a/b Faktor c: = a · c / b · c
Brüche kürzen: Zähler und Nenner werden durch dieselbe Zahl dividiert.
Beispiel: 12/16 dividiert durch 4 = 12 / 16 : 4 ––> 12 : 4 / 16 : 4 = 3/4.
Mit Buchstaben: a / b Divisor c: = a : c / b : c
Summen und Differenzen erweitern oder kürzen
Summen und Differenzen muss man vor dem Erweitern oder Kürzen berechnen.
Beispiel: 60 - 24 : 120 – 80 = (60 – 24) : (120 – 80) = 36 : 40 ––> kürzen mit 4 ––> 9/10
Einen Bruch in einen Dezimalbruch umwandeln:
Beispiel: 3/5 = 3 : 5 = 0,6
Einen Dezimalbruch in einen Bruch umwandeln:
Beispiel: 0,4 = 4/10 ––> kürzen mit 2 ––> 2/5
Aufgaben:
1. Erweitern: Die 4 Brüche sollen den Nenner 36 haben:
a) 3/4 b) 5/12 c) 10/18 d) 7/9
2. Kürzen: Die 4 Brüche sollen so weit gekürzt werden, bis eine weitere Kürzung nicht mehr möglich ist:
a) 21/63 b) 40/132 c) 25/200 d) 24/44
3. Brüche in Dezimalbrüche umwandeln: a) 12/60 b) 21/7 c) 9/42 d) 11/100
4. Dezimalbrüche in Brüche umwandeln: a) 0,1 b) 0,40 c) 0,60 d) 0,75
Lösungen
1. a) 27/36 b) 15/36 c) 20/36 d) 28/36
2. a) 1/3 b) 20/66 c) 5/40 d) 6/11
3. a) 0,20 b) 3,00 c) 0,213 d) 0,11
4. a) 1/10 b) 2/5 c) 3/5 d) 3/4