Lehrsatz des Pythagoras: Übungen 01.07.2010, 10:39
Der berühmte Satz des Pythagoras besagt: Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrats. In der Technik gibt es unzählige Formen, deren Abmessungen sich mit diesem Satz berechnen lassen. Hier Erläuterungen und ausgewählte Beispiele.
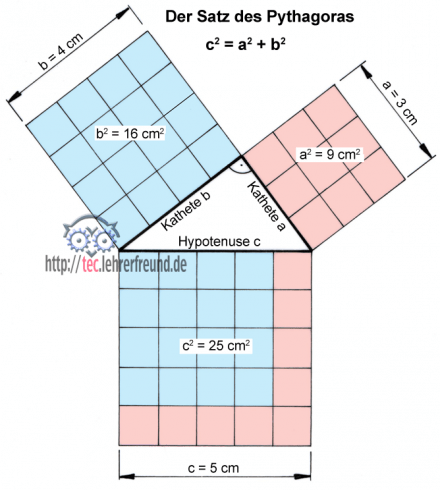
Der Satz des Pythagoras
Zeichnet man über den Katheten und der Hypotenuse eines rechtwinkligen Dreiecks Quadrate, dann gilt der Satz des Pythagoras: Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrats. Als Gleichung ausgedrückt:
c2 = a2 + b2
Ein besonderes rechtwinkliges Dreieck ist das mit glatten Seitenlängen, die man sich gut merken kann: 3, 4 und 5 cm. Die farbigen und gerasterten Quadrate bestätigen augenscheinlich die Richtigkeit des Satzes.
a und b sind die Längen der am rechten Winkel anliegenden Seiten, die Katheten; c bezeichnet die Länge der dem rechten Winkel gegenüber liegenden Seite, der Hypotenuse. Für das praktische Rechnen bedeutet der Satz: Sind im rechtwinkligen Dreieck zwei Seiten bekannt, kann man damit die unbekannte dritte Seite berechnen.
Die Umkehrung gilt ebenso: Die Länge der Hypotenuse ist gleich der Quadratwurzel aus der Summe der Kathetenquadrate, also:
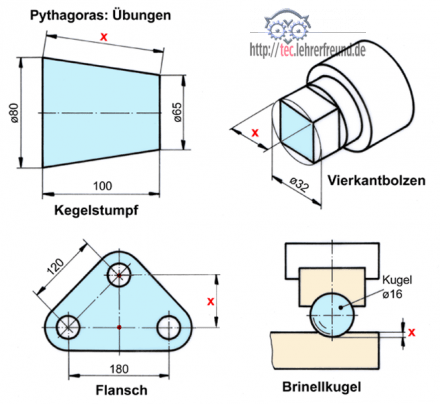
Übungen
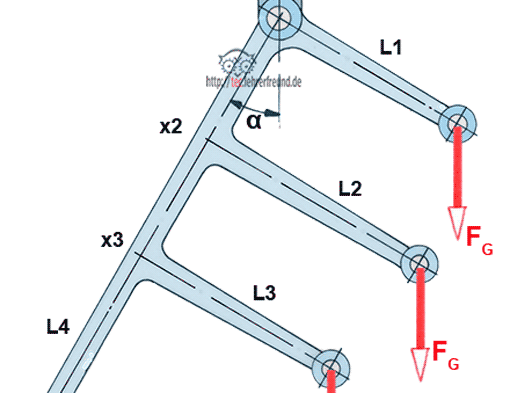
Kegelstumpf: Berechnen Sie die Mantellänge x.
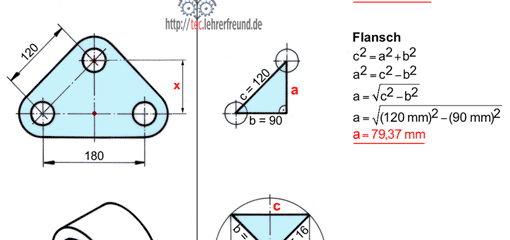
Flansch: Berechnen Sie den Abstand x.
Vierkantbolzen: Berechnen Sie die Schlüsselweite x. Die vier Eckkanten des Vierkants liegen auf der Mantellinie des Zylinders ø32.
Härteprüfung nach Brinell (schwedischer Ingenieur, 1900): Für die Härteprüfung von Werkstoffen gibt es mehrere Verfahren; eines davon ist die Brinellprüfung. Drückt man eine gehärtete Stahlkugel in den Werkstoff, dann bleibt ein kugeliger Eindruck, eine Kalotte. Ihr Durchmesser ist ein Maß für die Härte des Werkstoffs.
Berechnen Sie die Eindringtiefe x, wenn der Kugeleindruck einen Durchmesser von 7,8 mm hat.
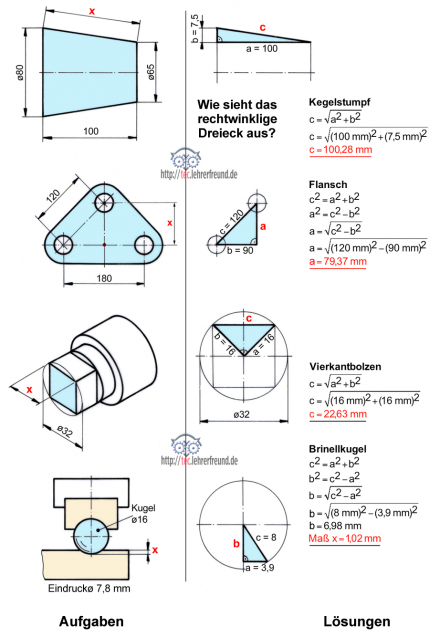
Lösungen
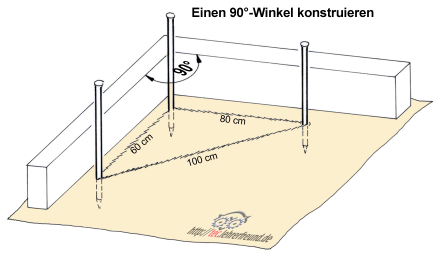
Das oben erwähnte 3 : 4 : 5 m-Dreieck lässt sich auch im täglichen Leben verwerten. Oft benötigt man z. B. im Freien rechte Winkel, sei es beim Bau eines Gartenhauses, bei der Anlage eines Zauns, eines Komposts, usw. Man schlägt zwei Eisenstäbe im Abstand von 3 m (oder Bruchteilen davon) entlang der gewünschten Grenze ein und legt über sie eine 12 m (= 3 m + 4 m + 5 m) lange zusammengeknotete Schnur. Wird der zweite Pfosten im Abstand von 4 m (oder Bruchteilen davon) bei gespannter Schnur eingeschlagen, ergibt sich ein einwandfreier rechter Winkel.
Wenn man mit dem Meterstab arbeitet - und das wird die Regel sein, dann empfehlen sich Maße, die innerhalb der Meterstablänge liegen, also z. B. 60 cm - 80 cm - 100 cm.