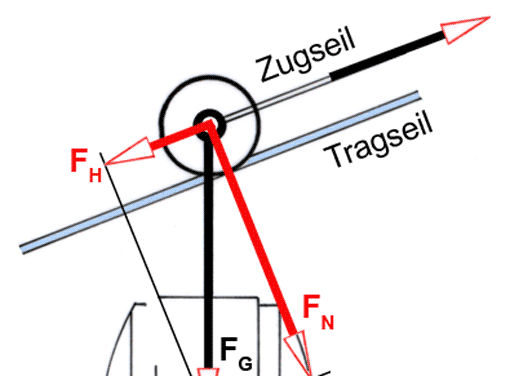
Reibzahl und Reibwinkel 26.07.2012, 07:09
Die Reibung ist eine häufig zu beobachtende Erscheinung in Natur und Technik und tritt in den verschiedensten Formen auf. Wir betrachten sie unter dem Gesichtspunkt des Reibwinkels ρ.
Lernniveau: Technische Oberschule, Berufskolleg u. Ä.
Reibzahl und Reibwinkel
Wir wiederholen Aussagen aus dem Beitrag Reibung (1) Grundlagen:
Die Reibung ist eine häufig zu beobachtende Erscheinung in Natur und Technik und tritt in den verschiedensten Formen auf. Durch Versuche kann man einige wichtige Gesetze der Reibung zwischen zwei festen Körpern finden:
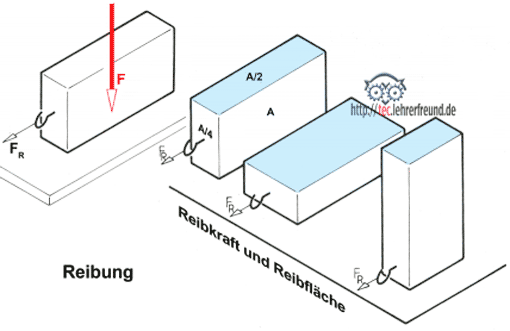
- Die Reibkraft FR ist bei gleichen Stoffen unabhängig von der Größe der Gleitflächen. Diese merkwürdige Erscheinung lässt sich nur damit erklären, dass auch glatte, ebene Flächen unabhängig von ihrer Größe jeweils nur in drei Punkten aufliegen.
- Bei nicht allzu großer Gleitgeschwindigkeit ist die Reibung FR unabhängig von der Geschwindigkeit zwischen den beiden Flächen.
- Bezeichnet man die senkrecht zur Unterlage wirkende Kraft als Normalkraft FN, dann kann man sagen: Die Reibkraft FR ist proportional der Normalkraft FN, mit der die beiden Flächen aufeinander gedrückt werden.
- Man unterscheidet Gleit- und Haftreibung. Haftreibung ist größer als Gleitreibung. Reibung ist proportional der Normalkraft (Anpresskraft) und unabhängig von der Flächengröße, jedoch abhängig vom Werkstoff und der Oberflächenrauigkeit.
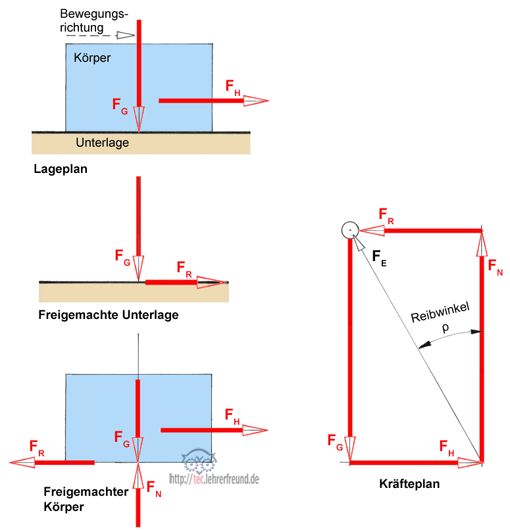
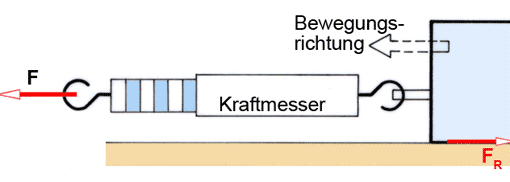
Zeichnung: Ein Körper drückt mit einer Kraft FG (entspricht der Normalkraft FN) senkrecht auf die Gleitfläche (in der Zeichnung der Lageplan) und wird durch die Verschiebekraft FH mit gleichförmiger Geschwindigkeit nach rechts bewegt. Wird der Körper verschoben, dann überwindet er die Gleitreibkraft FR. Die Kraft FR wirkt immer tangential zur Bewegungsfläche; dabei hemmt sie die Körperbewegung bzw. versucht, die Unterlage mitzunehmen.
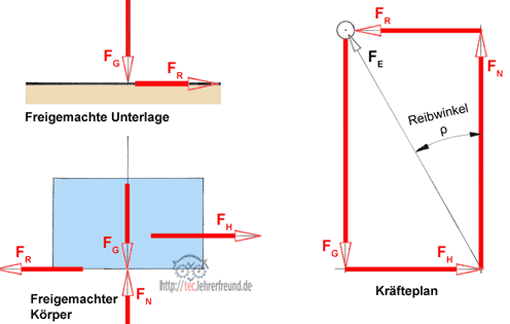
Den bewegten Körper freimachen: Die Richtung der Reibkraft FR ist in bezug auf den bewegten Körper gegen die Bewegungsrichtung einzutragen, denn sie wirkt bewegungshemmend. In bezug auf die (ruhende) Unterlage wirkt sie jedoch in Bewegungsrichtung.
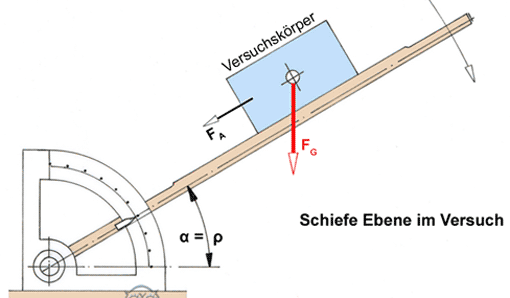
Aus dem Kräfteplan kann man ablesen: tan ρ = FR : FN ––> FR = FN • tan ρ
Der Reibwinkel ρ zwischen der Ersatzkraft FE und FN bestimmt die Größe von FR. Man bezeichnet tan ρ = μ als Reibzahl oder Reibungskoeffizient.
Gleitreibzahl μG = tan ρ
Als Berechnungsformel für die Gleitreibung erhält man also:
Gleitreibung FR = Normalkraft FN mal Reibzahl μG:
FR = FN . μG
Bleibt der Körper unter der Wirkung von FH in Ruhe (d. h. haftet er auf seiner Unterlage, wobei der Reibungswinkel ρG von Null bis auf einen Höchstwert ρH anwächst), spricht man von der Haftreibzahl:
Haftreibzahl μG = tan ρH.
Die Haftreibzahl ist größer als die Gleitreibzahl: μH > μG, weil sich die Oberflächenrauigkeiten im Stillstand ineinander verhaken können. Dadurch entsteht eine größere Haftwirkung.
Man sieht: Die Reibkraft FR ist immer nur ein Bruchteil der Normalkraft FN; seine Größe hängt vom Reibwert ab.
Unten einige Gleitreibzahlen μG, trocken, zwischen verschiedenen Werkstoffen. In Klammern die Gradzahlen für den Reibwinkel ρ:
Werkstoff
Stahl auf Stahl 0,15 (Reibwinkel ρ = 8,5°)
Stahl auf Gusseisen oder Bronze 0,18 (10,2°)
Stahl auf Eis 0,014 (0,8°)
Holz auf Holz 0,3 (16,7°)
Holz auf Metall 0,5 (26,6°)
Gummiriemen auf GG 0,4 (21,8°)
Textilriemen auf GG 0,4 (21,8°)
Bremsbelag auf Stahl 0,5 (26,6°)
Lederdichtungen auf Metall 0,2 (11,3°)
In einem weiteren Beitrag gehen wir auf eine Versuchsanordnung ein, mit der Reibzahlen bestimmt werden.