Reibung (2): Haftreibung, Gleitreibung, Rollreibung 14.03.2011, 10:56

Die Reibung ist ein in der Mechanik durchgängig anzutreffendes Phänomen. Die Reibung wirkt zwischen Gleitflächen in Lagern, Kupplungen, Führungen, Gewinden usw.

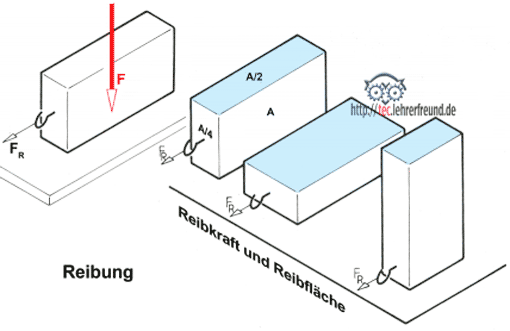
Reibung

Wie im Beitrag »Reibung (1): Grundlagen« erläutert, ist die Reibung ein in der Mechanik häufig anzutreffendes Phänomen; sie wirkt zwischen Gleitflächen in Lagern, Kupplungen, Führungen, Gewinden usw. Man unterscheidet Haft-, Gleit- und Rollreibung. Wie man bei der Vermittlung des mathematischen Hintergrunds der Reibung im Unterricht vorgehen kann, zeigt der erwähnte Beitrag ebenfalls.

Haftreibung, Gleitreibung

Haftreibung liegt vor, wenn zwischen den Gleitflächen - wie z. B. bei einer Kupplung - keine Bewegung stattfindet. Gleitreibung tritt zwischen Teilen auf, die sich gegeneinander bewegen, z. B. bei Gleitlagern zwischen Lagerzapfen und Lagerschale.
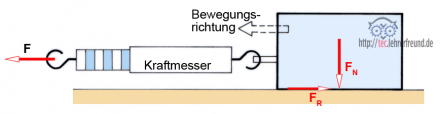
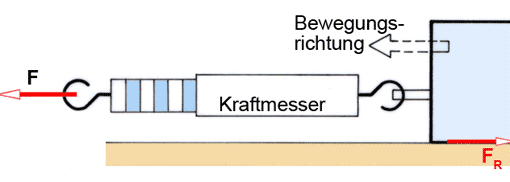
Die Haftreibungskraft ist größer als die Gleitreibungskraft. Die Reibungskraft F_R wirkt gegen die Bewegungsrichtung (Bild). Sie hängt ab von
- der Belastung der Gleitfläche durch die Normalkraft F_N,
- der Oberflächenqualität, der Werkstoffpaarung und dem Schmierzustand. Die genannten Größen sind zusammengefasst in der Reibungszahl μ (griech. mü).

Rechenbeispiel 1:
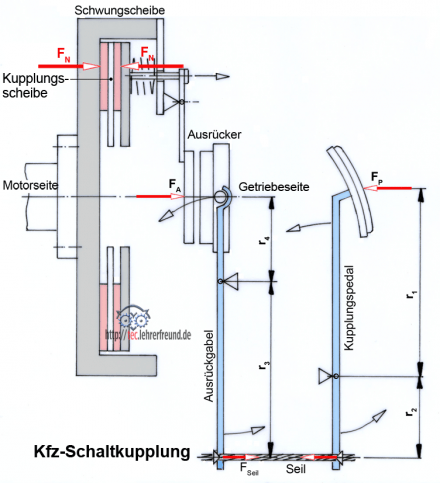
Die federbelastete Druckplatte und die Schwungscheibe drücken mit F_N = 180 daN auf die Reibbeläge. (Die von der Schwungscheibe ausgeübte Kraft ist nicht als eigenständige Kraft zu betrachten; sie ist die Reaktion auf die von rechts wirkende Druckplattenkraft). Der mittlere Reibdurchmesser ist 200 mm. Wie groß sind

a) die Reibungskraft F_R bei einer Reibungszahl μ = 0,45,
b) das auf die Getriebewelle übertragene Drehmoment M?

Lösungen

a) F_R = μ • F_N = 0,45 • 1800 N = 810 N

b) M = 2 • M_R (zwei Reibflächen)
M = 2 • F_R • r = 2 • 810 N • 100 mm = 162 000 N • mm = 162 Nm

Rechenbeispiel 2: 
Fräsmaschinenschlitten. Das Schlittengewicht F_G (= F_N) = 360 daN verteilt sich ungleichmäßig auf die beiden Gleitbahnen. Die Reibzahl wird mit 0,25 angegeben. 

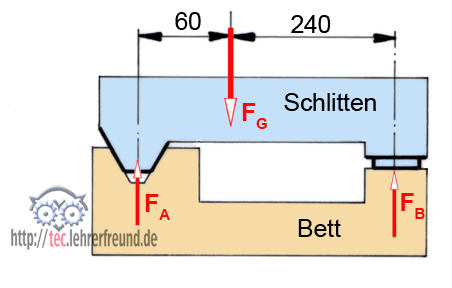
Zu berechnen sind
a) die Bahnkräfte F_A und F_B, 

b) Grobe Näherungsrechnung, wenn die V-Führung als eben betrachtet wird (wie die rechte Führungsbahn): Die Reibungskraft F_R, die der Verschiebekraft des Schlittens entgegen wirkt. 

c) Genaue Rechnung mit V-Führung, V-Winkel α = 90°. (Rechnung mit höherem Schwierigkeitsgrad).

Lösungsvorschläge:   

a) Anwendung des Hebelgesetzes, Drehpunkt in B.

F_A • 300 mm = F_G • 240 mm

F_A = 288 daN  –> F_B = 72 daN

b) F_R = F_N • μ = 360 daN • 0,25 = 90 daN 

c) Die genaue Berechnung muss Rücksicht auf die V-Führung nehmen. Aus α = 90° ergeben sich zwei auf die Gleitbahnen wirkende Normalkräfte F_N1 und F_N2. 

Sie sind F_N1 = F_N2 = F_A/2 : sin 45° = 203,7 daN. Die daraus entstehende Verschiebekraft F_HA = 2 • F_N1 • μ = 2 • 203,7 daN • 0,25 = 101,8 daN. Dazu kommt die Verschiebekraft F_HB = F_B • μ = 72 daN • 0,25 = 18 daN. F_HA + F_HB = 119,8 daN. Der bei der Näherungsrechnung c) gemachte Fehler würde also bei gut 30% liegen. 

F_HA ist größer als F_HB. Daraus entsteht in der waagrechten Verschiebe-Ebene ein Drehmoment. Um es auszugleichen, muss der Angriffspunkt der Verschiebekraft näher bei der V-Führung liegen.

Rollreibung

Die Rollkraft F überwindet die elastischen Verformungen zwischen einem rollenden Rad und seiner Unterlage. Dabei drückt sich das Rad etwas in die Unterlage ein und muss beim Rollen fortwährend über die Kante D gekippt werden (Bild; die Eindrücktiefe ist übertrieben groß dargestellt).

Aus der Momenten-Gleichgewichtsbedingung um den Punkt D erhält man

F • a = F_N • f

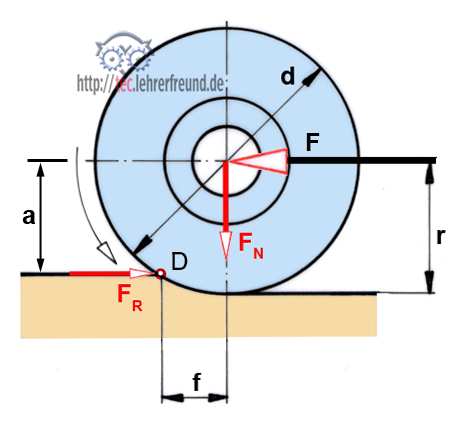
Weil der Kippabstand a und der Radius r annähernd gleich groß sind, kann man schreiben:

Rollkraft F = F_N • f / r

F hängt also ab von der Normalkraft F_N, der Rollreibungszahl f und dem Radius r der Rolle. Je größer der Rollendurchmesser d (= 2 r), desto kleiner die Rollkraft F. Bei ungleicher Lastverteilung und mehreren Rollen, zum Beispiel bei Wälzlagern, wird anstelle der Rollreibungszahl f die Reibungszahl μ ermittelt. Die Reibungskraft F_R  berechnet man aus
F_R = μ • F_N.

Beispiel:
Das Laufrad eines Schienenfahrzeugs hat einen Durchmesser d = 280 mm und wird mit F_N = 38 kN belastet.
Wie groß ist die Rollkraft F bei einer Rollreibungszahl f = 0,5 mm?

Lösung:   

F =  F_N • f / r = 38 000 N • 0,5 mm : 140 mm

F = 136 N

______________________________________________________

Seilreibung

Die Reibung von über Rollen laufenden Seilen ist ein spezielles und (mathematisch) anspruchsvolles Kapitel, das wir hier nur kurz streifen wollen.
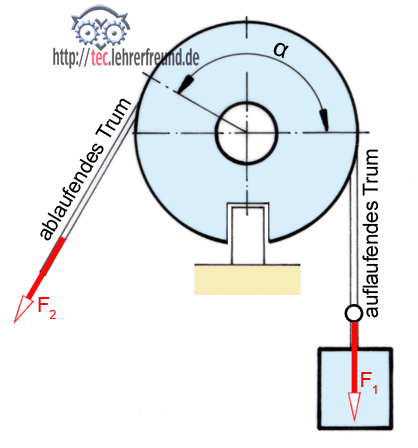
Seilreibung liegt vor, wenn um eine gegen Drehung gesicherte Scheibe ein vollkommen biegsames Zugmittel gelegt ist. Wegen der Reibung zwischen Zugmittel und Scheibe wird die Spannkraft F₂ am ziehenden (ablaufenden) Trum größer als die Spannkraft F₁ am gezogenen (auflaufenden) Trum:
F₂  = F₁ • e^μα

e ist die Basis des natürlichen Logarithmus (e = 2,718…)

μ = Reibzahl zwischen Zugmittel und Scheibe;
α = 2 • π  • α°/360° = α°/57,3° = Umschlingungswinkel im Bogenmaß.

__________ 

Diesem Beitrag folgen weitere Übungen zur Vertiefung.

__________

Siehe auch Reibung (1)