Deutsch im naturwissenschaftlich-technischen Unterricht (2): Technische Analyse 22.08.2015, 06:51

In der Reihe »Deutsch im naturwissenschaftlich-technischen Unterricht« wenden wir uns drei Aufgabentypen zu: der technischen Analyse, oft als Funktionsanalyse gemeint, dem technischen Experiment und Konstruktionsaufgaben.
2. Wortschatz im technischen Unterricht: Technische Analyse
|
Welche Aufgaben sind zu lösen? |
In Beschreibungen, die man von Nichttechnikern im Alltag hört, verwenden diese wenn nicht unrichtige Bezeichnungen, so doch oft unklare, immer wieder auch veraltete, ungebräuchliche Fachbegriffe. Einige Beispiele dafür:
Kraftfahrzeug: Die immer noch als Lichtmaschine bezeichnete Einrichtung ist ein Generator. Er ist nicht nur für die Beleuchtung eines Kraftfahrzeugs, sondern für die Energie im gesamten elektrischen Bordnetz zuständig.
Von einem Lager haben wir eine genauere Vorstellung, wenn es als Gleitlager oder Wälzlager bezeichnet wird.
Spricht jemand von Eisen, dann meint er in weit über 90% der Fälle Stahl.
Der Mann/die Frau auf der Straße darf sich das alles leisten, aber der Fachmann meistens nicht.
Viele in der Technik verwendete Fachbegriffe sind genormt. Dennoch hört man für dasselbe Teil oder denselben Vorgang an unterschiedlichen Orten unterschiedliche Bezeichnungen, sei es in verschiedenen Technikbereichen, in verschiedenen Berufen, ja, sie verändern sich oft sogar von Landstrich zu Landstrich. Beispiel: Die Schraube, die nach Norm Sechskantschraube (DIN EN 24017) heißt, hält sich hier und dort hartnäckig als »Maschinenschraube«.
Wir nehmen hier drei verschiedene Aufgabentypen unter die Lupe und werden feststellen: In allen dreien haben sich bestimmte Fachbegriffe etabliert.
Die Aufgabentypen sind:
– die technische Analyse, oft als Funktionsanalyse gemeint,
– das technisches Experiment,
– die Konstruktionsaufgabe.
In technischen Analysen finden wir häufig Fachbegriffe wie Baugruppe, Bauteil, Normteil, Funktion, Montage, Demontage, Kraft, Drehmoment, Drehbewegung.
Typische Verben sind
– bei Antrieben: antreiben, übertragen auf, weitergeben an, bremsen, beschleunigen ... usw.
– in der Statik: freimachen, Kräfte ermitteln, ersetzen, wirken, ... usw.
– in Festigkeitsfragen: dimensionieren, beanspruchen, wirken, entgegenwirken, angreifen, ... usw.
| Solche Begriffe sollte/n der/die Lehrende/n systematisch verwenden und üben. Dies fördert die Aneignung sprachlicher Muster, die den Schülern später das Lernen insofern erleichtern, als sie sich dann besser auf den eigentlichen Stoff konzentrieren können. |
Wir vertiefen das Thema am Beispiel »Pedalantrieb«.
Der Antrieb eines Fahrrads ist ein jedermann bekanntes technisches System. Seine physikalisch-mathematische Seite soll ein Schüler in einem Vortrag vor der Klasse in Einzelheiten herausarbeiten. Er soll dabei folgende Fachbegriffe verwenden: Drehmoment, Kräfteparallelogramm, Totpunkt, Tretkraft, Winkelfunktionen Sinus und Cosinus, wirksamer Hebelarm, Wirkungslinie.
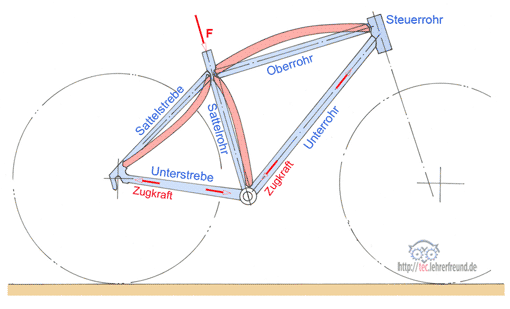
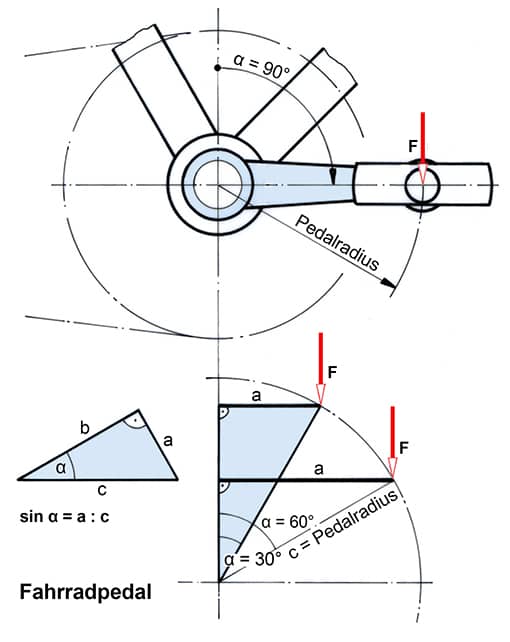
Die folgende vereinfachte Zeichnung zeigt ein Fahrradpedal; der Fuß des Radfahrers erzeugt beim Treten des Pedals eine Kraft. Es geht um die Frage, wie sich die Tretkraft auf die Drehwirkung am Zahnkranz und damit an der Kette auswirkt, wenn das Pedal in den drei verschiedenen Positionen a, b und c steht.
Das Thema ist im tec.LF unter https://www.lehrerfreund.de/technik/1s/fahrrad-kraefte-und-drehmomente-am-pedal/4273 zu finden.
Vorschlag für einen Schülervortrag
Auszubildender: »Meine Aufgabe ist es, Euch die an einem Fahrradantrieb wirkenden Kräfte und Drehmomente zu erläutern. Schwerpunkt ist dabei die physikalisch-mathematische Seite des Pedalantriebs. Später werden wir unsere Erkenntnisse mit einer Berechnung vertiefen.
Ich gehe davon aus, dass das Kräfteparallelogramm jedem bekannt ist. Auch was man unter einem Drehmoment versteht, müsste Euch geläufig sein.«
 :
:
Bild 4: Dreiecke für die Berechnung des Sinus und des Cosinus
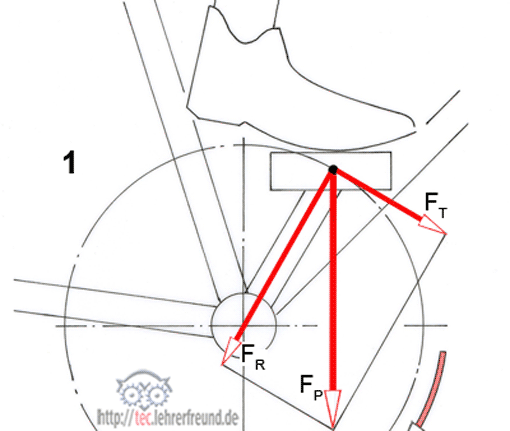
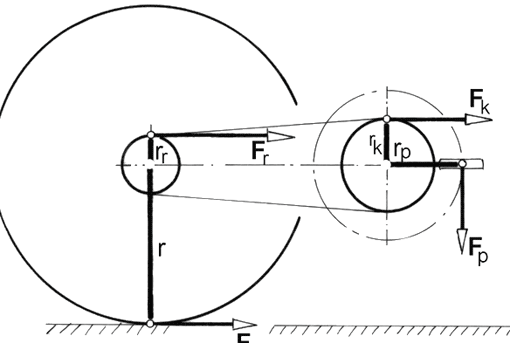
Bilder 1 und 2:
Die Bauteile eines Pedalantriebs sind:
– die Tretlagerwelle
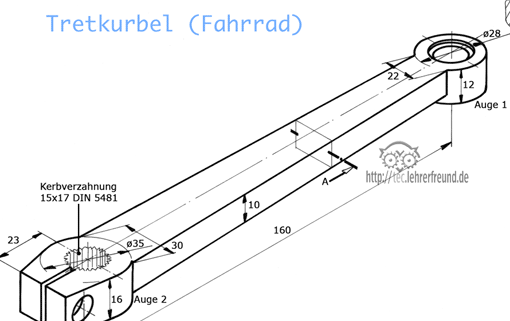
– die Tretkurbel
– das Kettenblatt
– das Pedal mit Pedalachse.
Tretlagerwelle, Tretkurbel, Pedalachse und Kettenblatt bilden eine fest miteinander verbundene Baugruppe.
Beim Treten übt der Fuß eine Kraft FP auf das Pedal aus. FP wird, weil ein wirksamer Hebelarm vorhanden ist, von der Tretlagerwelle in ein Drehmoment umgewandelt. Dieses Drehmoment steht auch am Zahnkranz zur Verfügung.
Die Drehwirkung ist umso größer, je größer1) die Tretkraft FP und je länger der Hebelarm l1 ist. Das Produkt aus Kraft und Hebelarm nennt man Drehmoment: M = FP • l1; es wird in der Einheit Newtonmeter (= Nm) gemessen. Der wirksame Hebelarm ist der senkrechte Abstand zwischen der Wirkungslinie der Kraft und dem Drehmittelpunkt der Tretlagerwelle.
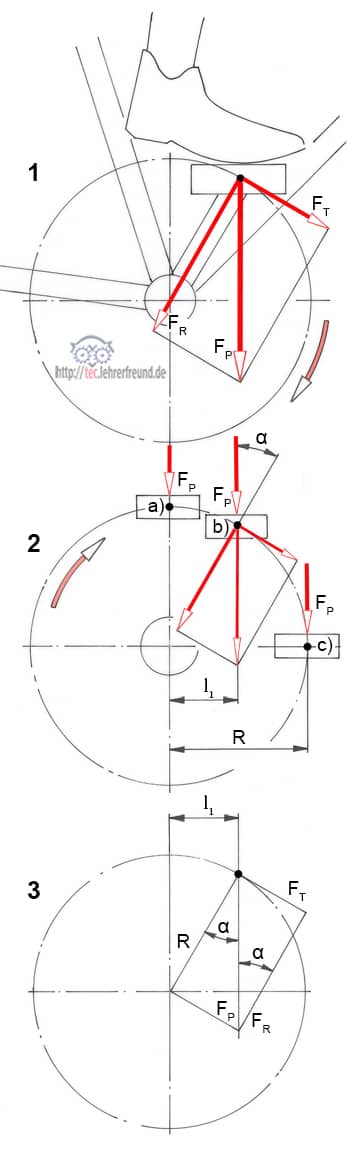
Sieht man sich das Kräfteparallelogramm mit den Kräften FP, FR und FT an (Bild 1), erkennt man, dass durchgängig nur FT dem Vorwärtsfahren zugute kommt. Der zur Lagermitte hin gerichtete Kraftanteil FR bleibt für das Fahren wirkungslos, denn er erzeugt an der Tretlagerwelle kein Drehmoment. Er belastet nur das Lager.
FT = Tangenzialkraft; FR Lagerkraft.
Im Bild 2 sind drei Tretpositionen eingezeichnet:
– Pedalstellung a: Im oberen Totpunkt ist das Drehmoment Null (M = 0), weil FP durch die Lagermitte geht und deshalb kein Kraftarm vorhanden ist.
– Pedalstellung b: Der senkrechte Abstand von der Wirkungslinie der Pedalkraft FP zum Drehpunkt ist l1 = sin α • R. Im Tretlager wirkt also das Drehmoment M = FP • l1. Dieselbe Wirkung ergibt sich aus FT • R, weil R und FT einen rechten Winkel miteinander bilden.
– Pedalstellung c: M = FP • R.
Bilder 3 und 4: Kräfte- und Hebelverhältnisse am Pedal.
sin α = FT : FP = l1 : R
cos α = FR : FP –> FP = FR : cos α
M = FT • R = FP • l1
l1 = sin α • R
Die Analyse zeigt: Während einer Umdrehung des Pedals verändert sich die Drehwirkung dauernd; d. h. die erzeugten Drehmomente haben in jeder Pedalposition einen anderen Wert. Dementsprechend ist auch die Antriebskraft am Hinterrad in jeder Tretposition unterschiedlich.
1) Sprache: Das leidige desto ..., umso ..., je ...
Immer wieder hört man von Rednern, die es eigentlich besser wissen müssten, Sätze wie :
• »Desto größer der Hebelarm, desto größer das Drehmoment«. Oder:
• »Umso langsamer ein Auto fährt, desto geringer ist sein Benzinverbrauch«.
So geht das nicht – aber wie sagt man es richtig?
Zum meist vorne stehenden Bindewort (= Konjunktion) »je« gehören die Partnerwörter desto oder umso. In der Anwendung heißt dies:
• Je größer der Hebelarm, desto (umso) größer das Drehmoment. Oder:
• Je langsamer ein Auto fährt, desto (umso) geringer ist sein Benzinverbrauch.
Aber auch dies ist möglich:
• Die Drehwirkung ist umso größer, je größer die Tretkraft ist.
Früher war gebräuchlich: Je länger, je lieber, was heute als veraltete Form gilt.
Ich untermauere meine Erklärungen mit Rechenbeispielen.
Die Kurbel sei 170 mm lang. Der Fuß des Fahrers übe in jeder Position eine senkrecht nach unten wirkende Kraft FP mit dem Betrag 220 N aus.
Wie groß sind die Drehmomente im oberen Totpunkt, nach 30°, nach 60°, in der waagrechten Stellung des Pedals?
Lösungsvorschlag:
Oberer Totpunkt: M = 0, weil die Kraft FP durch die Tretlagermitte geht .
α = 30° ––> Bild 4: a = c • sin α = 0,17 m = 0,085 m.
M = FP • a = 220 N • 0,085 m = 18,7 Nm
Gleicher Rechenweg bei 60° und 90°:
α = 60°: M = 32,4 Nm
α = 90°: M = 37,4 Nm
Im Beitrag wurden diese Fachbegriffe verwendet:
Nomen:
Drehmoment, Drehpunkt, wirksamer Hebelarm, Kraftarm, Kräfteparallelogramm, Lagerkraft, Newtonmeter, Tangenzialkraft, Wirkungslinie,
Verben:
belasten, umwandeln, wirken
Adjektive:
senkrecht, wirksam, wirkungslos
Arbeitsblatt
Wir schlagen vor, für alle Beiträge Arbeitsblätter vorzubereiten. Diese sollen
– äußerlich gleich gestaltet sein,
– in den Aufschrieben etwa demselben Schema folgen (Bild unten).
Die Arbeitsblätter werden, wie üblich, vom Lehrer ausgearbeitet, und – wie gewohnt – von den Schülern für ihre Aufschriebe benutzt.
Wenn die Skizzen und Zeichnungen einfach sind, stellen die Schüler sie selbst her. Schwierigere werden in den Arbeitsblättern vorgegeben.
Ein Arbeitsblatt könnte so aussehen: