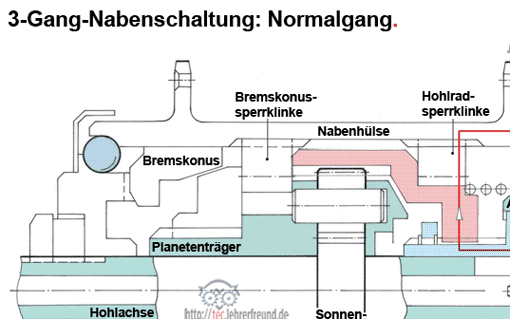
Kräfte am Fahrrad 19.01.2012, 15:17
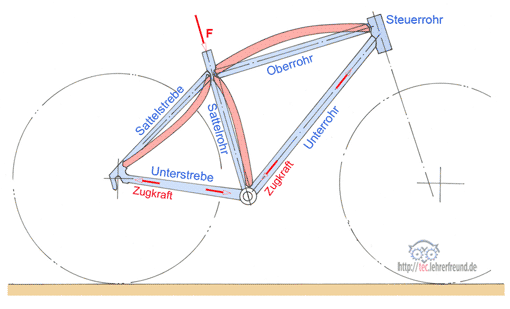
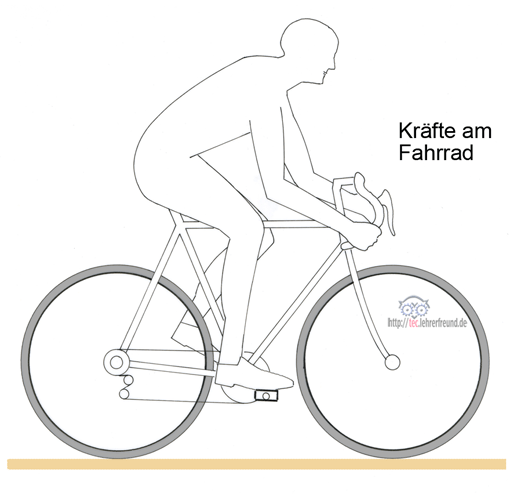
Der Fahrradrahmen muss Kräfte aufnehmen, die sich aus dem Fahrergewicht, dem Treten und durch Fahrbahnstöße ergeben. Aus Versuchen kennt man die zulässigen Lasten, bei denen - wenn man sie nicht überschreitet - Rahmenverformungen oder Brüche auszuschließen sind.
Welche Kräfte beanspruchen ein Fahrrad?
Wie gut oder wie schlecht man mit einem Fahrrad fährt, bestimmt nicht zuletzt die Rahmenform; dies gilt besonders für hoch belastete Räder wie etwa Rennräder.
Der Fahrradrahmen muss Kräfte aufnehmen, die sich aus dem Fahrergewicht, dem Treten und durch Fahrbahnstöße ergeben. Aus Versuchen kennt man die zulässigen Lasten, die - wenn man sie nicht überschreitet - kaum zu Rahmenverformungen oder Brüchen führen.
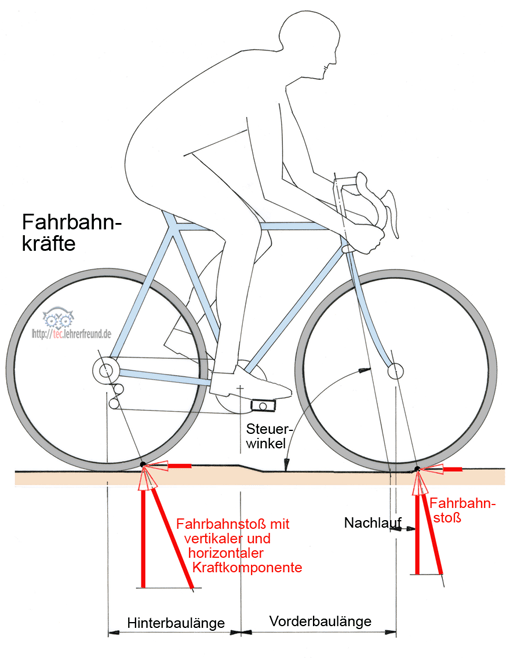
Vertikal- und Horizontalkräfte
Beim Überfahren von Unebenheiten entstehen Fahrbahnstöße auf die Laufräder und Ausfallenden; sie äußern sich als mehr oder weniger vertikale Kräfte.
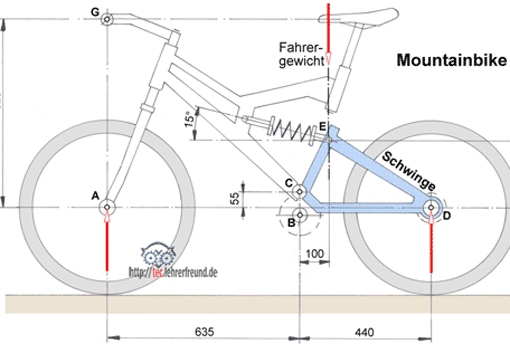
Beim Rennrad können dabei Vertikalkräfte bis 7500 N und beim ungefederten Mountainbike bis 9000 N über das Hinterrad in den Rahmenhinterbau eingeleitet werden. Bei der weniger belasteten Gabel liegen diese Werte entsprechend unter den genannten Werten.
Die Horizontalkomponenten von Stoßkräften durch Unebenheiten der Fahrbahn dürfen den Rahmen nicht verformen. Bei Auffahrunfällen wirken Kräfte in horizontaler Richtung; sie führen in der Regel zu plastischen Verformungen von Gabel und Rahmen. Dabei ist es in kritischen Fällen - wie übrigens auch beim Autofahren - für den Fahrer günstig, wenn durch plastische Verformungen die Wucht des Aufpralls durch Energieumleitung gemindert wird.
Plastisch verformt wird ein Körper, wenn er nach Wegnahme der Belastung seine neue Form beibehält. Die Horizontalkräfte bleiben unter 2000 N am Hinterrad und höchstens 1000 N an der Gabel. Die Unterstreben des Hinterbaus werden vorwiegend auf Zug beansprucht, der für die Rahmenteile ungefährlich bleibt.
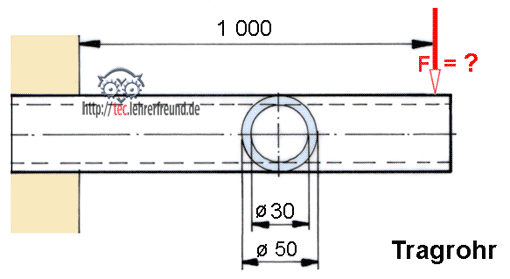
Bei horizontaler Belastung wird die Gabel wie ein einseitig eingespannter Träger auf Biegung beansprucht. Die auftretenden Biegemomente sollen 750 Nm nicht übersteigen.
Biegemoment: Ein Bauteil wird auf Biegung beansprucht, wenn in einem bestimmten Abstand von der Einspannung eine Kraft wirkt. Das Biegemoment hat die Einheit Newtonmeter (Nm).
Zur Biegebeanspruchung liest man im tec.LEHRERFREUND-Beitrag Biegefestigkeit:
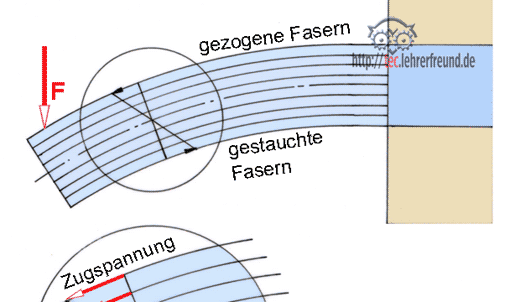
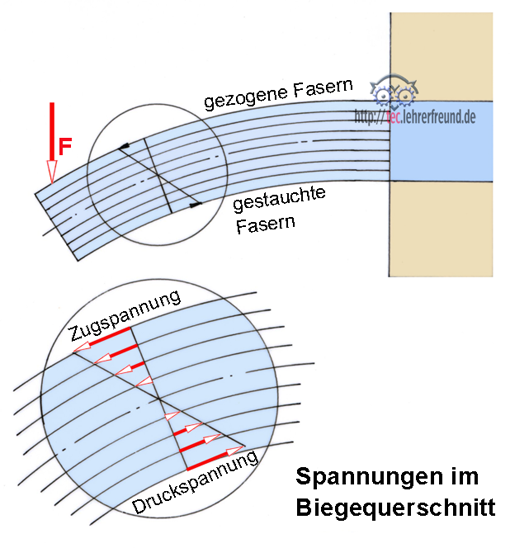
Bild unten: Die Kraft F beansprucht den Stab (auch Welle, Balken u. Ä.) auf Biegung. Die vor der Belastung gerade Stabachse wird gebogen. Unter einer Biegebelastung entstehen im Querschnitt Zug- und Druckspannungen. Anmerkung: Um den Vorgang deutlich zu machen, sind die Durchbiegungen in den Skizzen stark übertrieben.
In den Randfasern entstehen die stärksten Spannungen, die neutrale Faserschicht (strichpunktiert) dagegen ist spannungslos. In symmetrischen Querschnitten sind die Zug- und Druckspannungen gleichmäßig (linear) über den Querschnitt verteilt.
Die Biegespannung σb ist abhängig
- vom Biegemoment Mb
- vom Widerstandsmoment W.
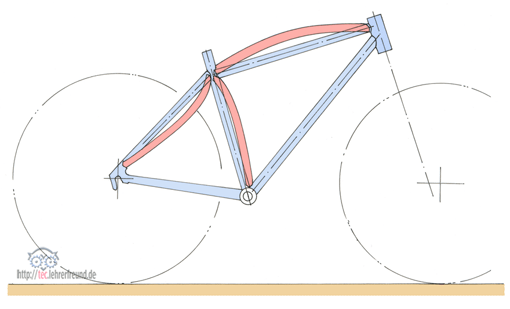
Wie wirken Biegemomente auf den Rahmen? An dem schräg nach hinten verlaufenden Sattelrohr entstehen am Sattelknoten Biegemomente bis 1000 Nm. Ober- und Sattelrohr und die beiden Sattelstreben nehmen dieses Moment auf und biegen sich elastisch. Die Biegeverformungen können einige Millimeter erreichen.
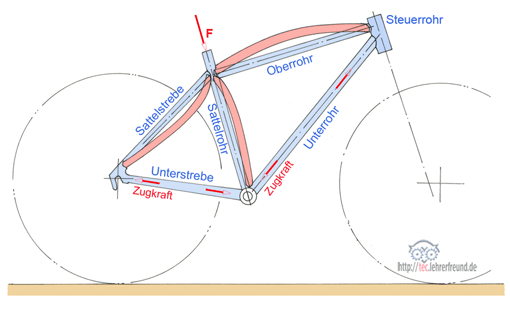
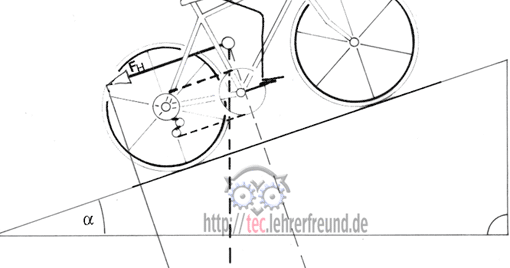
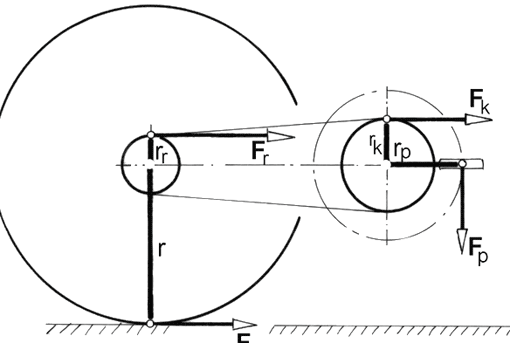
Bild unten: Biegung an der Gabel. Aus den Kräften FV und FH mit ihren Hebelarmen lV und lH ergeben sich die beiden Biegemomente MV = FV • lV und MH = FH • lH.
Rechnerische Beziehung:
FV • lV = FH • lH.
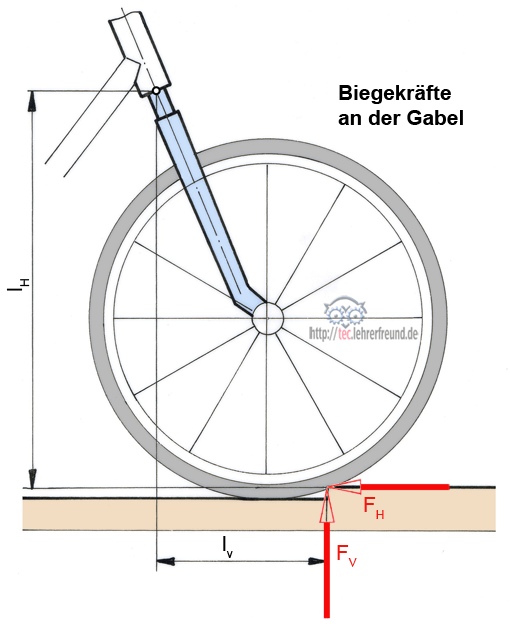
Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.