Festigkeitsberechnungen (5): Übungsaufgaben zu Biegung 20.12.2010, 10:31

Welche Maximalspannungen treten bei auf Biegung beanspruchten Rohren und Rechteckquerschnitten auf? Beispielrechnungen.

Biegung: Übungsaufgaben

Fortsetzung des Beitrags »Festigkeitsberechnungen (4): Biegung« 

Zu Beginn wiederholen wir eine Anmerkung aus einem voraus gehenden Beitrag:
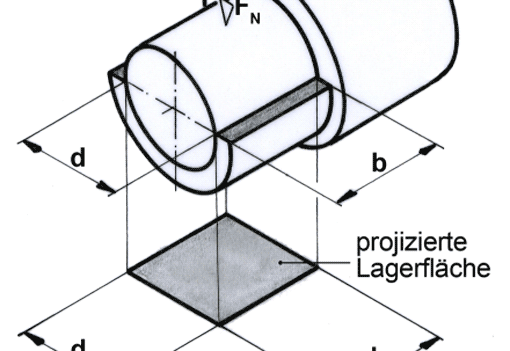
Widerstandsmoment und Trägheitsmoment sind Größen, die dem Anfänger erfahrungsgemäß einige Schwierigkeiten bereiten, denn er kann sich nur wenig darunter vorstellen. Der Begriff Trägheitsmoment und die Einheit »cm⁴« werden ihn völlig verwirren. Er muss sich aber nicht mehr darunter vorstellen als dass er hier einfach eine von der Querschnittsform abhängige Rechengröße einsetzen muss. Ein einfacher Versuch gibt hierüber Aufschluss.

In der Skizze »Flachstahl: Widerstandsmoment und Werkstückhöhe« hat der Stab in beiden Fällen denselben Querschnitt b x h und wird jeweils von derselben Kraft F gebogen. Trotzdem wird er sich weniger verformen, wenn er wie in der Skizze unten, hochkant eingespannt ist. Diese Erkenntnis wird in der Berechnung mit dem Widerstandsmoment W berücksichtigt.

Bei den folgenden Aufgaben empfiehlt es sich, die Biegemomente in Ncm zu berechnen, weil die Widerstandsmomente üblicherweise in cm³ angegeben werden.

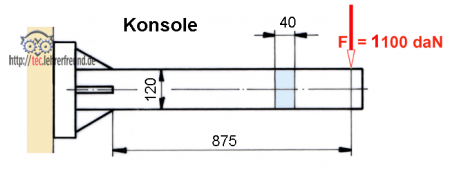
Konsole:

Wie groß ist die Biegespannung?

Formel Biegespannung σ_b = M_b : W   in N/cm²

M_b= F ∙ l = 11 000 N ∙ 87,5 cm = 962 500 Ncm

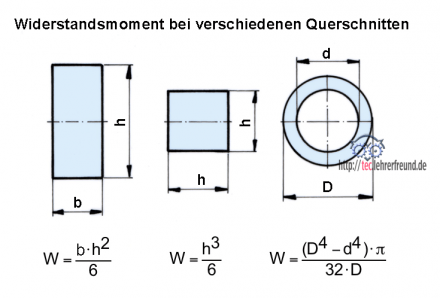
Widerstandsmoment W = b ∙ h² : 6 = 4,0 cm ∙ (12 cm)² : 6 = 96 cm³ =

Biegespannung σ_b = M_b : W = 962 500 Ncm :  96 cm³ =

σ_b =  10 026 N/cm² ≈ 100 N/mm²

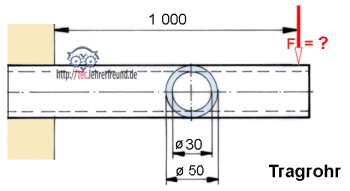
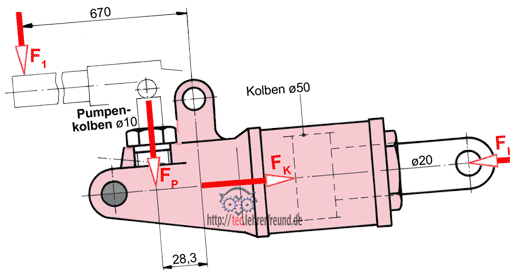
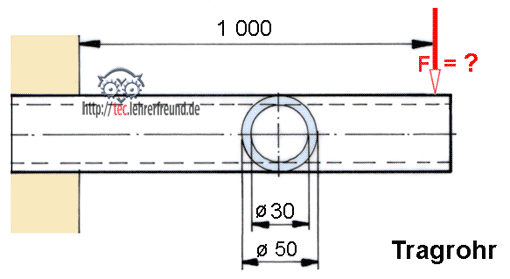
Tragrohr: 

Wie groß ist die Last F in daN, wenn die Biegespannung 100 N/mm² nicht überschreiten soll?

Biegespannung σ_b = M_b : W  –> M_b= F ∙ l

σ_b = F ∙ l : W

F =  σ_b ∙ W : l

Widerstandsmoment W = (D⁴ - d⁴)  ∙ π : 32 : D

W = (5⁴ - 3⁴)  ∙ π : 32 : 5 (Längenmaße in cm)

W = 10,68 cm³

F = σ_b ∙ W : l = 10 000 N/cm² ∙ 10,68 cm³ : 100 cm = 

F = 1 068 N = 106,8 daN

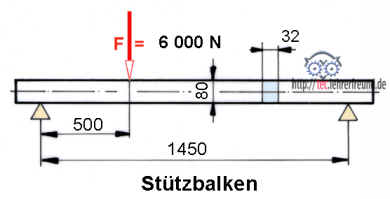
Stützbalken: 

Wie groß ist die Biegespannung?

Biegespannung σ_b = M_b : W

M_b= F_A ∙ l

Hier muss man zuerst die linke Stützkraft F_A berechnen. Der Drehpunkt des Hebels wird ins rechte Lager gelegt.

M_rechts = M_links

F_A ∙ 1 450 = F ∙ 950

F_A = 6 000 N ∙ 950 mm : 1 450 mm = 3 931 N

M_b= F_A ∙ 50 cm = 3 931 N ∙ 50 cm

M_b = 196 552 Ncm

Widerstandsmoment W =  b ∙ h² : 6 = 3,2 cm ∙ (8 cm)² : 6 =

W = 34,13 cm³

Biegespannung σ_b = M_b : W = 196 552 Ncm : 34,13 cm³ =

σ_b = 5 759 N/cm² = 57,6 N/mm² 

^{____________________} 

^{In WIKIPEDIA http://de.wikipedia.org/wiki/Widerstandsmoment lesen wir:} 

Als Widerstandsmoment  wird in der technischen Mechanik eine allein aus der Geometrie (Form und Maße) eines Balkenquerschnitts abgeleitete Größe bezeichnet. Sie ist ein Maß dafür, welchen Widerstand ein Balken bei Belastung der Entstehung innerer Spannungen entgegensetzt.

Bei der Belastung Biegen wird vom axialen oder Biegewiderstandsmoment  gesprochen, beim Verwinden (Torsion) vom polaren oder Torsionswiderstandsmoment .

Das Widerstandsmoment eines Querschnitts steht in einfachem geometrischen Zusammenhang mit dem Flächenträgheitsmoment, mit dessen Hilfe bei der Querschnitts-Bemessung die Verformung eines Balkens bei Belastung berechnet wird (siehe auch Steifigkeit). Widerstandsmoment und Flächenträgheitsmoment sind, in Abhängigkeit von den typischen Abmaßen geometrisch einfacher Flächen und standardisierter Materialprofile (z. B. Stahlprofile), in allgemeinen technischen Handbüchern enthalten, oft in gemeinsamen Tabellen.