Kräfte am Mobilbagger 20.10.2016, 05:46

Statikaufgabe. An einem Mobilbagger sollen unbekannte Kräfte berechnet werden.

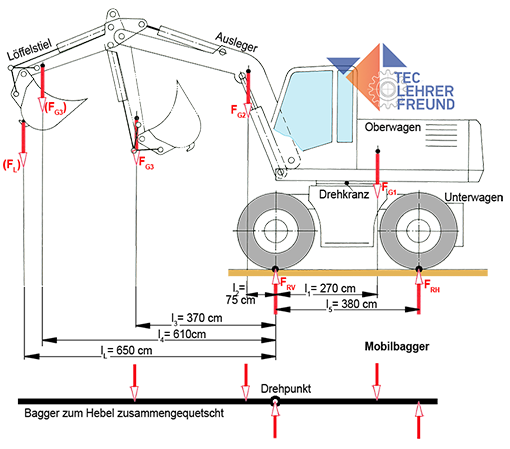
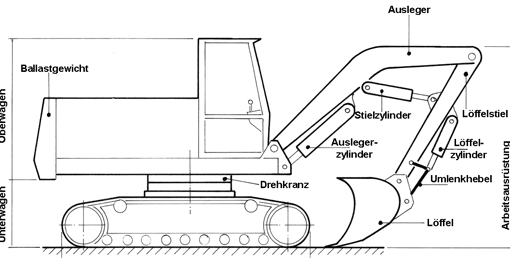
Kräfte am Bagger 

Gegeben:
F_G1 = 64 kN
F_G2 = 10 kN 
F_G3 = 6 kN

Aufgabe 1

Der Löffelstiel ist eingefahren. Sein Abstand von der Vorderradmitte ist l₃ = 370 cm. Zu berechnen sind: 

1a) die Radaufstandskräfte F_RV und F_RH. Der Hebel in der Skizze unten mit Drehpunkt in F_RV soll die Entscheidung erleichtern, in welcher Richtung die einzelnen Kräfte drehen.

1b) die Last (F_L), die der Bagger (gerade noch) heben kann, wenn der Löffelstiel ausgefahren ist (l_L = 650 cm).

Lösungsvorschlag 
Aufgabe 1a)

Achskraft F_RH berechnen: 
Momentengleichgewicht:
ΣM_RV = 0 = F_RH • l₅ – F_G1 • l₁ + F_G2 • l₂ + F_G3 • l_{3 ⇒} 

F_RH = (F_G1 • l₁ – F_G2 • l₂  – F_G3 • l₃) : l₅ 

F_RH = (64 kN • 270 cm – 10 kN • 75 cm – 6 kN • 370 cm) : 380 cm = 

F_RH = 37,66 kN

Achskraft F_RV berechnen:

ΣFy = 0 = F_RV + F_RH – F_G1 – F_G2 – F_G3 ⇒

F_RV =  – F_RH + F_G1 + F_G2 + F_G3  

F_RV = – 37,66 kN + 64 kN +10 kN + 6 kN

F_RV = 42,34 kN 

1b) F_L berechnen

Kippbedingung: F_RH = 0 d.h. die Hinterräder beginnen gerade abzuheben. F_G3 ist nach (F_G3) gewandert.

ΣM_RV = 0 = (F_L) • l_L + (F_G3) • l₄ + F_G2 • l₂ – F_G1 • l₁ ) ⇒ 

(F_L) = (– F_G3) • l₄ – F_G2 • l₂ + F_G1 • l₁ ) : l_L 

= (– 6 kN • 610 cm – 10 kN • 75 cm + 64 kN • 270 cm ) : 650 cm 

(F_L) = 19,8 kN 

Aufgabe 2  
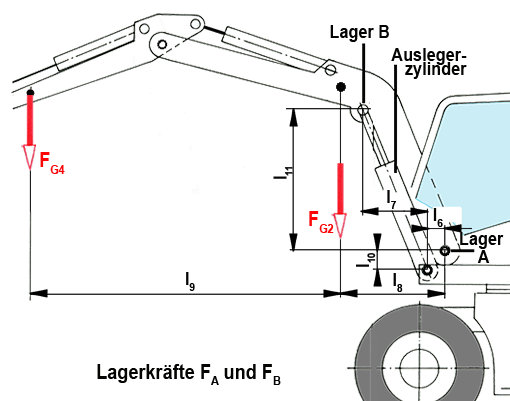
Berechnen Sie die Kräfte in den Lagern A und B (Skizze unten), wenn F_G4 = 9,0 kN 

Gegeben: 
l₆ = 35 cm
l₇ = 110 cm
l₈ = 180 cm
l₉ = 680 cm
l₁₀ = 300 cm
l₁₁ = 250 cm
F_G4 = 9 kN
F_G2 = 10 kN

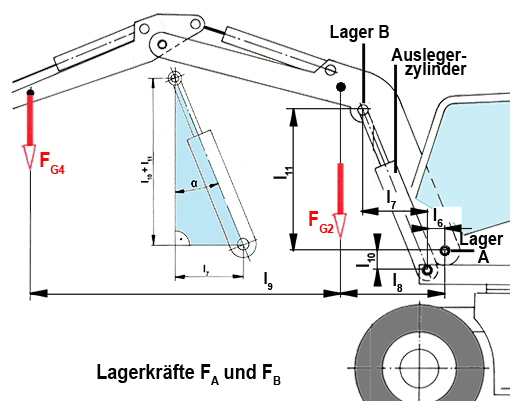
Neigung α des Auslegerzylinders

tan α = l₇ : (l₁₀ + l₁₁) = 110 cm : 550 cm = 0,2 ⇒ α = 11,31°  
sin α = 0,196; cos α = 0,98

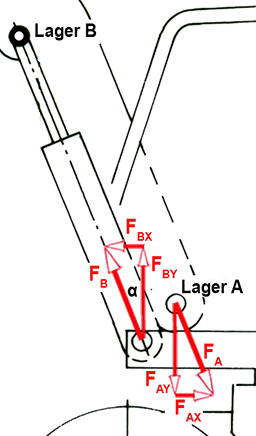
Drehmomente um Lager A ⇒ F_B 

ΣM_A = 0 = F_BX • l₁₁ – F_BY • l₇ + F_G2 • l₈ + F_G4 • (l₈ + l₉) 

               = F_B • sin α • l₁₁ – F_B • cos α • l7 + F_G2 • l8 + F_G4 • (l₈ + l₉) 

FB =  (– F_G2 . l₈  – F_G4 • (l₈ + l₉) ) : (sin α • l₁₁ – cos α • l₇) 

FB = (– 10 kN . 180 cm – 9 kN . 860 cm) : (0,196 . 250 cm – 0,98 . 110 cm) 

F_B = 162,24 kN 

Berechnung von F_A 

ΣF_X = 0 = FAX – FBX ⇒ F_AX = F_BX = F_B • sin α = 162,24 kN • 0,196 = 

F_AX = 31,8 kN 

ΣF_Y = 0 = F_BY – F_AY – F_G2 – F_G4

F_AY = F_BY – F_G2 – F_G4 

F_AY = F_B • cos α – F_G2 – F_G4  

F_AY = 162,24 kN • 0,98 – 10 kN – 9 kN

F_AY = 144,22 kN

F_A = √ F_AX² + F_AY² 

F_A = 165,33 kN

Aufgabe 3 

Der Auslegerzylinder hat einen Kolben mit 120 mm Durchmesser. Welcher Öldruck entsteht im Auslegerzylinder? 

Lösung  Druck p = F_B : A ⇒

A = d² • p : 4 = (12 cm)² • p : 4 = 113,1 cm² 

p = 162,24 kN : 113,1 cm² = 162 240 N : 113,1 cm² = 16 224 daN : 113,1 cm² = 143,45 daN/cm² 

p = 143,5 bar