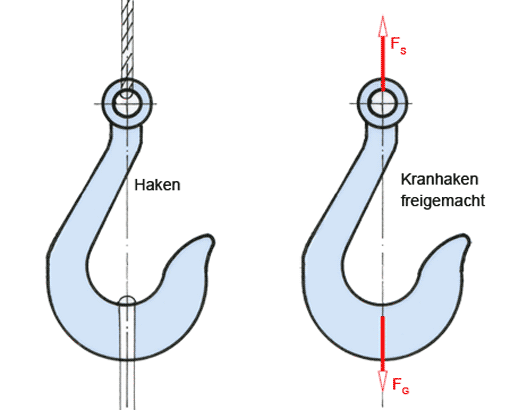
Allgemeines Kräftesystem: Rechnerische Gleichgewichtsbedingungen (2) 13.01.2012, 08:41

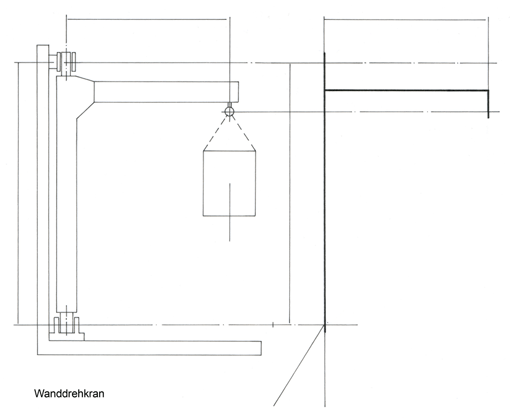
An einem einfachen Wanddrehkran berechnet: Der Kran ist im statischen Gleichgewicht, wenn die algebraische Summe aller x- und y-Komponenten gleich Null ist und wenn die algebraische Summe sämtlicher Momente für jeden beliebigen Drehpunkt ebenfalls gleich Null ist.

Fortsetzung des Beitrags »Allgemeines Kräftesystem: Rechnerische Gleichgewichtsbedingungen (1)« 

Beachten: Niveau Techn. Gymnasium, Berufskolleg u. Ä.

(Zur Erinnerung: Wanddrehkran, Hublast F_G = 2500 daN)

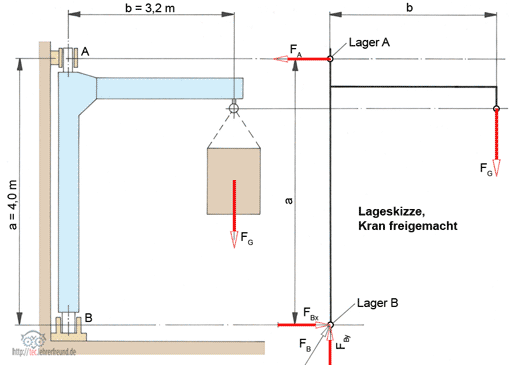
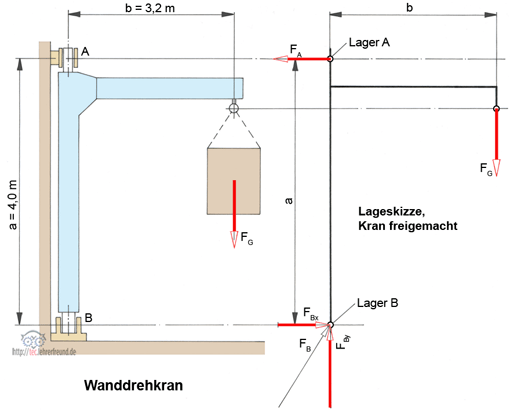
Nach der unmaßstäblichen Lageskizze des freigemachten Körpers (Wanddrehkran, rechte Skizze) stellen wir die Gleichgewichtsbedingungen auf:
I.   ∑F_x = 0 = - F_A + F_Bx;  –> F_Bx = F_A
II.  ∑F_y = 0 = - F_G + F_By ;  –> F_By = F_G
III. ∑M_(B) = 0 ¹⁾ = - F_A · a + F_G · b  –> F_A = F_G · b : a = 2 500 daN · 3,2 m : 4,0 m = 2 000 daN

F_Bx = F_A =  2 000 daN; F_By = F_G = 2 500 daN 

¹⁾ Zu lesen wie: Summe aller Momente um den Drehpunkt B gleich Null.

Zu beachten: Würde man die Richtungen der Kräfte F_A, F_Bx und F_By nach dem Gefühl wählen, könnte sich ein negatives Rechnungsergebnis ergeben (Minus-Vorzeichen). Dies würde bedeuten, dass die tatsächliche Kraftrichtung mit der angenommenen nicht übereinstimmt und nachträglich berichtigt werden muss.

Im Ansatz der Gleichgewichtsbedingungen ist es üblich, Kräfte, die nach rechts oder nach oben gerichtet sind, mit positiven Vorzeichen zu versehen, ebenso rechtsdrehende Momente. 

Wenn man den Momentenbezugspunkt (= Drehpunkt) für Gleichung III. ∑M_(B) = 0 in den Angriffspunkt unbekannter Kräfte legt, haben diese keine Drehwirkung und erscheinen somit in der Momenten-Gleichgewichtsbedingung nicht. Diese Gleichung enthält dann oft nur eine Unbekannte, die man sofort berechnen kann: Meistens bietet diese Gleichung (III.) den Schlüssel zur Lösung!
Zu berücksichtigen ist auch, dass jeder Punkt außerhalb der zu berechnenden Konstruktion benutzt werden darf, wenn er zu einer einfacheren Berechnung führt.  

Mit F_Bx und F_By können wir nun mit Hilfe des Satzes von Pythagoras auch die Lagerkraft F_B berechnen:  
F_B = √F_Bx² + F_By² = √2 000² daN² + 2 500² daN² = 
F_B = 3 201,6 daN

Hier noch eine Überlegung, die zusätzliche Gleichgewichtsbedingungen beinhaltet: 

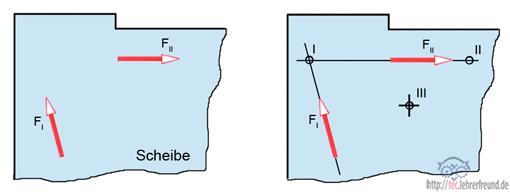
Auf die skizzierte Scheibe wirken die Kräfte F_I und F_II. An welcher Stelle sollten wir für die Berechnungen den Drehpunkt wählen?

Wir wählen den Drehpunkt an der Stelle I (Skizze rechts): Der Ansatz ∑M_(I) = 0 bringt kein Gleichgewicht, weil F_I nicht berücksichtigt ist. Um Punkt I dreht sich die Scheibe zwar nicht, kann sich aber unter der Wirkung der durch den Momentendrehpunkt gehenden Kraft verschieben.   

Wir wählen den Drehpunkt an der Stelle II: Mit ∑M_(II) = 0 wird zwar die Kraft F_I erfasst, aber auch hier könnte F_II den Körper verschieben.

Wir wählen den Drehpunkt an der Stelle III: Erst ∑M_(III) = 0 garantiert, dass die Scheibe im Gleichgewicht ist, weil nun auch die Kraft F_II berücksichtigt wird. Die Bedingung für die Wahl des geeigneten Drehpunkts ist, dass er nicht auf einer durch I und II gehenden Geraden liegt. 

Es gibt also zwei Möglichkeiten, im beliebigen Kräftesystem unbekannte Kräfte zu bestimmen: 

∑F_x = 0
∑F_y = 0
∑M  = 0

und

∑M_(I)  = 0
∑M_(II) = 0
∑M_(III) = 0    

______________________ 

Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.