Kettenräder berechnen 17.01.2014, 16:28
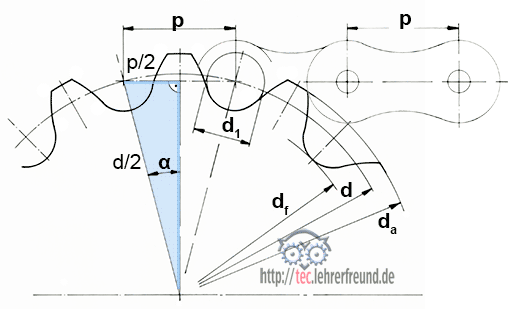
Bei Kettenrädern ist die Teilung p der gerade Abstand zwischen zwei Zähnen, also nicht das Bogenmaß wie bei Zahnrädern. Deshalb spielt hier das rechtwinklige Dreieck mit den Seiten d/2 (Hypotenuse) und p/2 (Gegenkathete) eine Rolle. Daraus ergibt sich eine andere Formel für d.
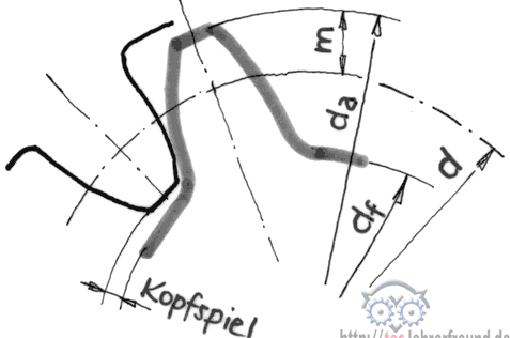
Das bestimmende Maß bei einem Zahnrad ist sein Teilkreisdurchmesser d. Auf dem Teilkreis liegt die Zahnteilung p als Bogenmaß. Der Modul ist das Verhältnis p : π ––> m = p : π. Die Formel für den Teilkreisdurchmesser ist d = m • z.
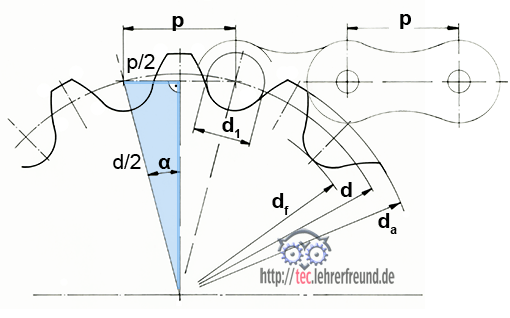
Bei Kettenrädern dagegen ist die Teilung p der gerade Abstand zwischen zwei Zähnen, also nicht das Bogenmaß. Deshalb spielt hier das rechtwinklige Dreieck mit den Seiten d/2 (Hypotenuse) und p/2 (Gegenkathete) eine Rolle. Diese Tatsache führt zu einer anderen Formel für d.
sin α = p/2 : d/2 = p : d. Daraus ergibt sich: d = p : sin α.
Bei einer Kettenrad-Zähnezahl z ist
α = 360° : (2 • z) = 180° : z ––>
d = p : sin (180° : z)
Beispielrechnung:
Kettenrad mit z = 19 Zähnen und einer Zahnteilung = Kettenteilung p = 1/2” = 12,7 mm.
Welchen Teilkreisdurchmesser d hat das Kettenrad?
d = p : sin (180° : z)
d = 12,7 mm : sin (180° : 19) = 12,7 mm : sin 9,474°
d = 12,7 mm : 0,1646 =
d = 77,16 mm
Um dem Anwender das Rechnen mit der Sinusfunktion zu ersparen, kann man ihm in einer Tabelle die bereits berechneten Werte vorgeben. Dabei wird in der Formel d = p : sin (180° : z) der Wert 1 : sin (180° : z) zu y zusammengefasst. Dann heißt die neue Formel
d = p • y
Wir geben hier die y-Werte für Zähnezahlen von z = 10 bis z = 25 an:
z = 10 y = 3,2361
z = 11 y = 3,5495
z = 12 y = 3,8637
z = 13 y = 4,1786
z = 14 y = 4,4940
z = 15 y = 4,8097
z = 16 y = 5,1258
z = 17 y = 5,4422
z = 18 y = 5,7588
z = 19 y = 6,0755
z = 20 y = 6,3925
z = 21 y = 6,7095
z = 22 y = 7,0267
z = 23 y = 7,3439
z = 24 y = 7,6613
z = 25 y = 7,9787
Bei z = 19 und p = 12,7 mm findet man für d:
d = p • y = 12,7 mm • 6,0755 = 77,16 mm (siehe auch Berechnung oben)