Hebel: Von der Länge zum Winkel 12.01.2014, 07:53
Hier wollen wir die Anfrage eines tec.LEHRERFREUND-Lesers übernehmen und sie als Beitrag behandeln. Es geht um eine Berechnung, die zeigen kann, wie man einen Rechenweg verfolgt, der einem zunächst vielleicht völlig schleierhaft ist. Dabei stellt man schließlich fest, dass sich die Lösung fast unerwartet in Schritten ergibt.
Hier wollen wir die Anfrage eines/r tec.LEHRERFREUND-Lesers/in übernehmen und zum Beitrag erheben. Es geht um eine Berechnung, die zeigen kann, wie man mit einem Rechenweg umgeht, der einem zunächst vielleicht völlig schleierhaft vorkommt. Dabei stellt man schließlich fest, dass man sich – fast unerwartet – der Lösung in Schritten nähert.
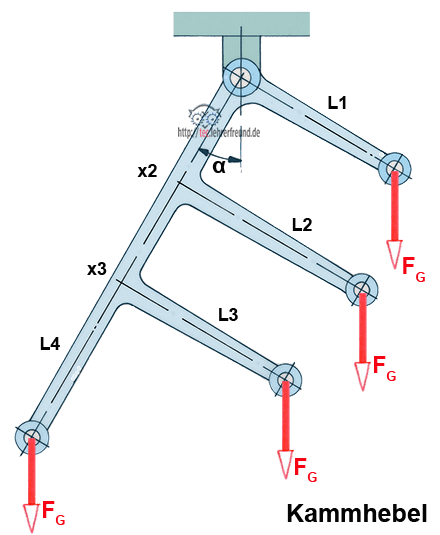
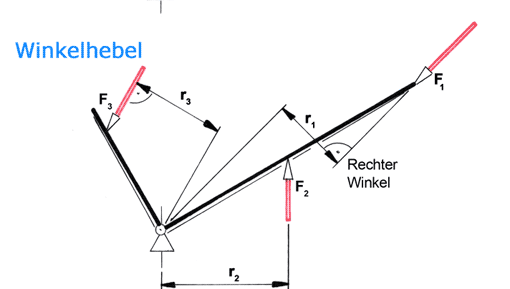
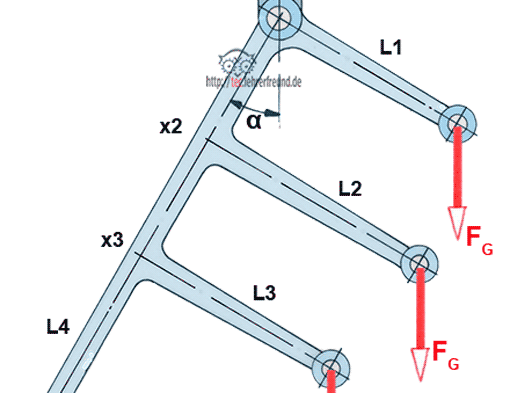
Der/die Leser/in hat sich mit dem Hebelgesetz beschäftigt. Dabei geht es um die oben abgebildete Konstruktion (Bild 1), die wir ihrer Form wegen einfach einmal als »Kammhebel« bezeichnen wollen. Er/sie möchte wissen: Gibt es eine Formel, mit der sich der Winkel α berechnen lässt, wenn man die Kräfte, die einzelnen Hebellängen und deren Positionen kennt? Dabei sollen die vier Hebelenden mit den vier gleich großen Zugkräften FG belastet werden.
(Wir übernehmen die Längenbezeichnungen, die uns der Leser angegeben hat).
Die Hebel L1, L2 und L3 bilden mit dem Hebel L4 einen rechten Winkel. Das Eigengewicht des Kammhebels soll in der Berechnung unberücksichtigt bleiben.
Ohne uns genauer mit der Berechnung auseinandergesetzt zu haben, ahnen wir: Die Sache läuft auf Winkelfunktionen hinaus. Warum? Die Lasten FG und die Hebel bilden keinen rechte Winkel zueinander, also wird uns der Winkel α wohl irgendwie belästigen.
Denkt man sich den Kammhebel als Spielzeug, das am oberen Drehpunkt aufgehängt ist, sehen wir dieses förmlich hin und her schwingen. Es sind also auch Drehmomente im Spiel.
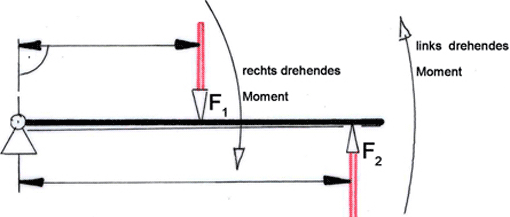
Den schwingenden Kammhebel bringen wir zur Ruhe, indem wir für Gleichgewicht am Hebel sorgen: Dafür muss die Summe (Σ) der rechtsdrehenden Momente gleich groß sein wie die Summe der linksdrehenden Momente (Bild 2):
ΣMrechts = ΣMlinks
FG • L4h = FG • L1h + FG • (L2h – x2h) + FG • (L3h – x3h) /: FG
(h ist die Abkürzung für horizontal). Die wirksamen Hebelarme L2h und L3h sind gegenüber L2 und L3 um x2h bzw. x3h kürzer.
Wir dividieren beide Seiten der Momentengleichung mit FG durch:
L4h = L1h + (L2h – x2h) + (L3h – x3h). Die Gleichung zeigt: Die Winkellage des Kammhebels wird nur durch die Hebel und ihre Abstände bestimmt.
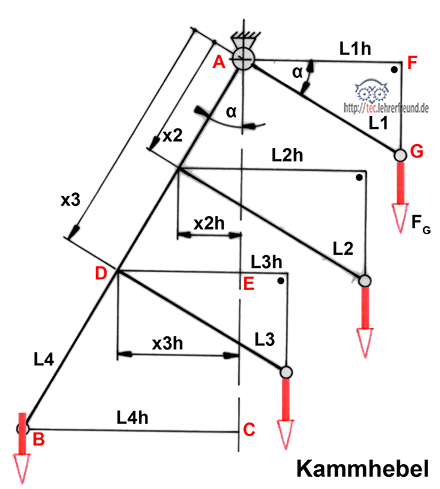
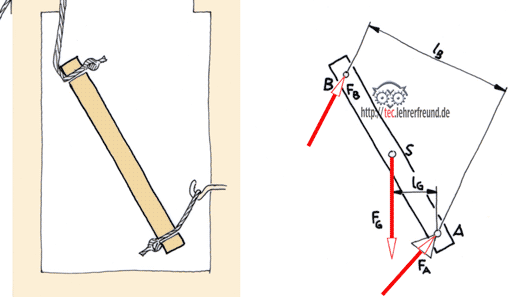
Gleichung 1: L4h = L1h + L2h – x2h + L3h – x3h. Keine der Horizontalkomponenten ist in der Anfangsskizze gegeben. Aber aus den Hebellängen und dem Winkel α können wir sie berechnen (Bild oben):
Gleichung 2: sin α = L4h : L4 ––> L4h = L4 • sin α (Dreieck ABC)
Gleichung 3: cos α = L1h : L1 ––> L1h = L1 • cos α (Dreieck AFG)
Gleichung 4: L2h = L2 • cos α
Gleichung 5: L3h = L3 • cos α
Gleichung 6: sin α = x2h : x2 ––> x2h = x2 • sin α, und
x3h = x3 • sin α (Dreieck AGH)
Die Gleichungen 2 bis 6 werden in die Gleichung 1 eingesetzt:
L4 • sin α = L1 • cos α + L2 • cos α – x2 • sin α + L3 • cos α – x3 • sin α
Wir ordnen die Gleichung nach sin α und cos α:
L4 • sin α + x2 • sin α + x3 • sin α = L1 • cos α + L2 • cos α + L3 • cos α
sin a • (L4 +x2 + x3) = cos α • (L1 + L2 + L3)
sin α : cos α =
tan α = (L1 + L2 + L3) : (L4 +x2 + x3)
Die Beziehung sin α : cos α = tan α lässt sich leicht erklären (Skizze unten):
sin α = a : c; cos α = b : c
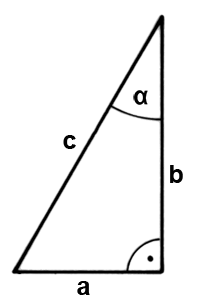 sin a : cos a = a : c / b : c = a : b = tan α
sin a : cos a = a : c / b : c = a : b = tan α