Kräftepaar und Drehmoment 16.11.2011, 13:51

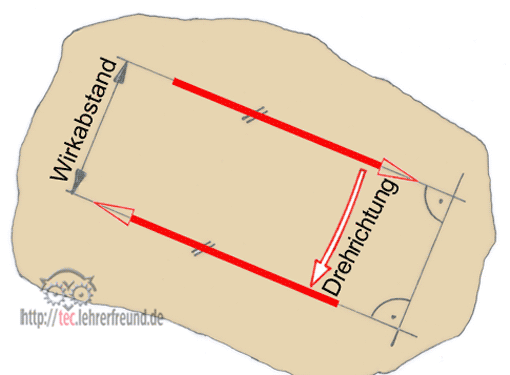
Entsteht als Reaktion auf eine Kraft eine zweite Kraft, die einen Abstand zur einleitenden Kraft besitzt wie etwa bei einer Handkurbel, dann hat man es mit einem Kräftepaar zu tun. Wie man mit Kräftpaaren umgeht.

Kräftepaar und Drehmoment

Zu jeder Kraft gehört eine Gegenkraft. Steht eine Maschine auf dem Boden, denkt man zunächst nur an eine Gewichtskraft, die auf den Boden drückt. Wo ist aber die Gegenkraft? Es ist die Kraft des Bodens, die dafür sorgt, dass die Maschine nicht einbricht. Diese Reaktionskraft liegt auf der gleichen Wirklinie wie die Gewichtskraft, ist von unten nach oben gerichtet und gleich groß wie die Gewichtskraft.
Nicht ganz so einfach ist der Fall, wenn zwischen Kraft und Gegenkraft ein Abstand liegt wie beispielsweise bei der Handkurbel.

Das Kräftepaar        
Entsteht als Reaktion auf eine Kraft eine zweite Kraft, die einen Abstand zur einleitenden Kraft besitzt wie zum Beispiel bei der Handkurbel, dann hat man es mit einem Kräftepaar zu tun. 

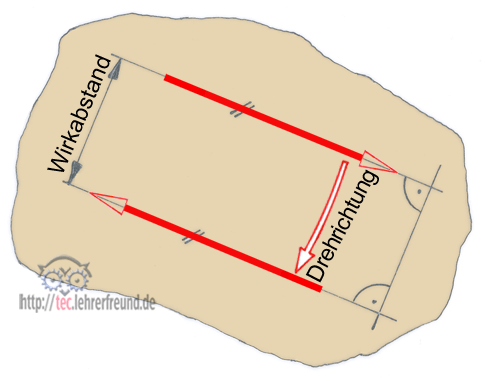
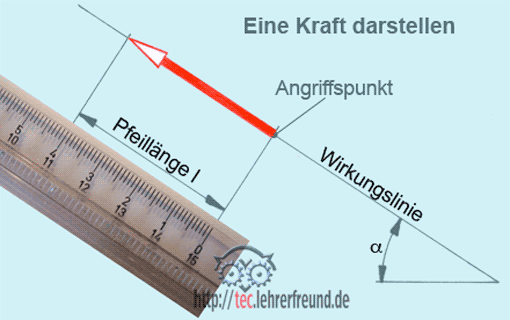
Ein Kräftepaar besteht aus zwei gleich großen, parallelen und gegensinnigen Kräften, zwischen deren Wirkungslinien der Wirkabstand a liegt. a wird senkrecht zu den Wirkungslinien gemessen. Ein solches Kräftepaar wirkt immer dann, wenn sich ein Körper dreht oder ohne Bindungen drehen würde; diesen Fall finden wir bei Zahnrädern, Riemenscheiben, Tretkurbeln, Handkurbeln, Handrädern, Drehstabfedern usw. 

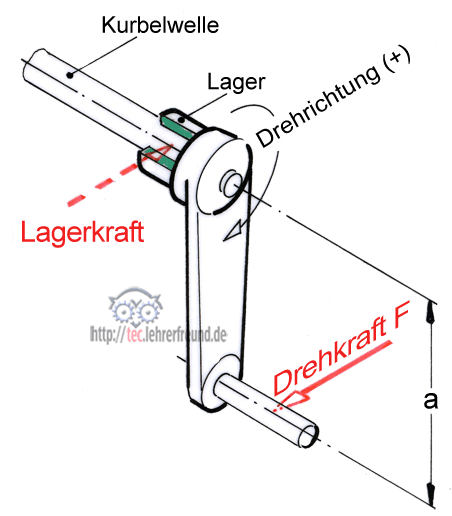
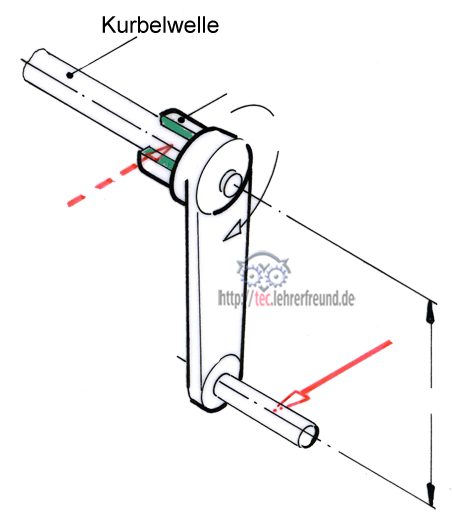
Betrachten wir eine Handkurbel etwas näher. Es ist ein Irrtum, zu meinen, die Handkurbel drehe sich ausschließlich unter der Wirkung der Handkraft oder Drehkraft F. Würde man das Lager wegnehmen, wäre die Drehbewegung nicht möglich, es sei denn, wir stützten die Kurbelwelle an der Lagerstelle mit der freien Hand ab. Beim Drehen der Kurbel entsteht ein Kräftepaar. Die zweite Kraft eines Kräftepaars ist, wie in diesem Beispiel, sehr oft eine Lagerkraft, die man in der Regel aber nicht einzeichnet.
In der Technik wird in vielen Fällen allein die Größe der Drehkraftwirkung einer Einzelkraft in Bezug auf einen Drehpunkt verlangt.
Eine Anregung: Man macht sich im Zweifelsfall an einer Lageskizze klar, wie die Wirkungslinie der Kräfte (oder der Kraft) und der senkrechte Wirkabstand liegen.
Die Größe der Drehwirkung eines Kräftepaares spürt man unmittelbar, wenn man versucht, z. B. einen Fahrradlenker an seiner (senkrechten) Drehachse festzuhalten. Dabei ist die Drehkraftwirkung umso größer, je größer die Kraft am Lenkergriff wird, und je größer man den Wirkabstand a zwischen den beiden Kräften macht, das heißt je weiter außen wir am Lenker anfassen.

Die Drehkraftwirkung eines Kräftepaares nennt man sein Drehmoment (auch »statisches Moment«). Seine Größe wird durch das Produkt aus der Kraft F und ihrem senkrechten Wirkabstand a bestimmt:
Drehmoment = Kraft mal senkrechten Kraftabstand vom Drehpunkt (Kraft mal Hebelarm)

M = F • a [Nm, Ncm].      

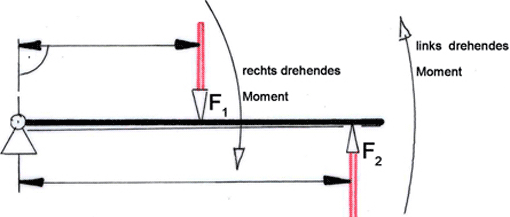
Die Drehrichtung wird durch die Vorzeichen berücksichtigt: (+) = rechts drehend und (–) = links drehend.

Man erkennt, dass die Erklärung für das Drehmoment einer Kraft in Bezug auf einen bestimmten Drehpunkt zum gleichen Ergebnis führt wie die Betrachtung mit dem Kräftepaar. Man sollte sich im Geiste immer die zweite Kraft hinzudenken, auch wenn man sie nicht braucht. Ohne sie könnte man leicht groben Rechenfehlern erliegen. 

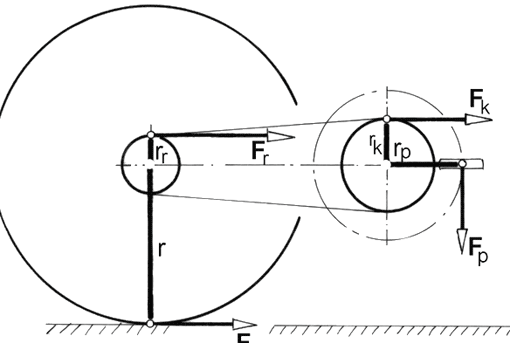
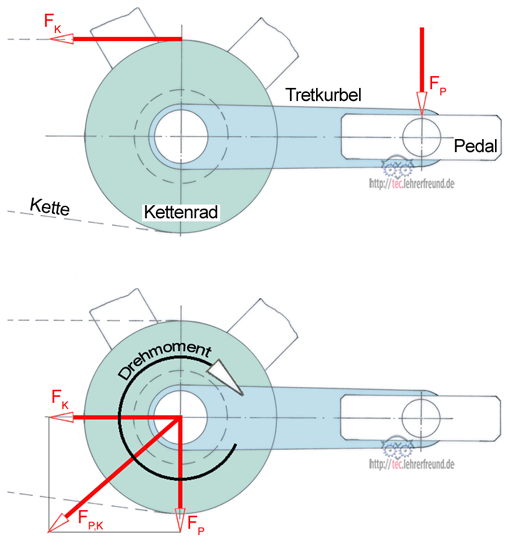
Die folgende Skizze einer Kurbelwelle zeigt, welche Wirkung die Kurbelkraft F auf den Drehpunkt M der Kurbelwelle hat.

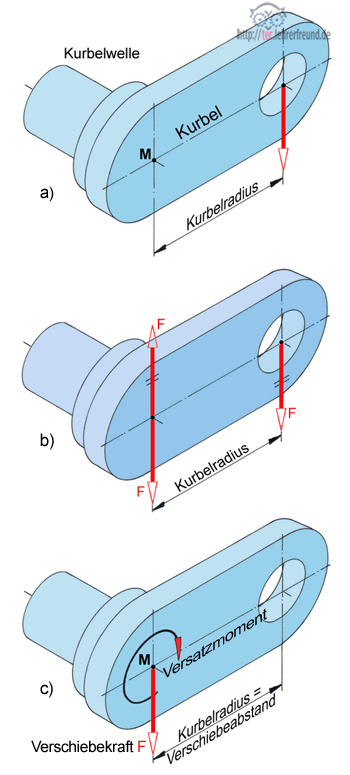
a) Am Kurbelradius wirkt F 

b) Wir legen in die Wellenmitte M zwei gleich große, aber gegensinnige Kräfte F. Da sie sich aufheben, hat sich an der Gesamt-Kraftwirkung nichts geändert.

c) Wir fassen die beiden gestrichenen Kräfte zu einem Kräftepaar zusammen und ersetzen sie durch ein Momenten-Drehsymbol. 

Erkenntnis: Das Kräftesystem mit der am Kurbelradius wirkenden Einzelkraft F besteht aus einem Drehmoment und einer Einzelkraft, die jetzt in M wirkt. Verschiebt man eine Einzelkraft, muss in jedem Fall ein so genanntes Versatzmoment = Einzelkraft mal Verschiebeabstand hinzugefügt werden. 

Eine Kraft am Hebelarm verursacht also immer eine Verdrehung der Kurbelwelle und eine Verschiebung der Einzelkraft, die vom Lager aufgenommen werden muss.

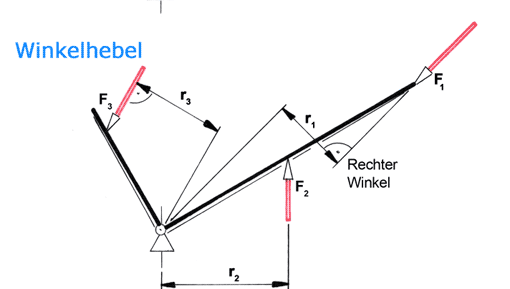
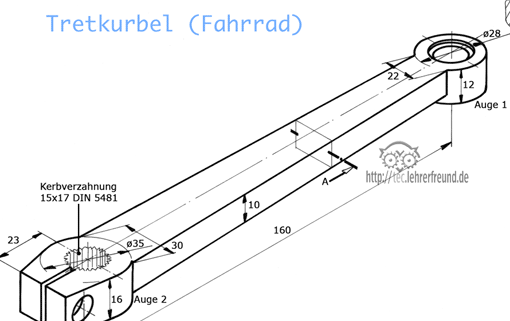
Wie sich Drehmomente am selben Objekt verändern, kann man an der Tretkurbel eines Fahrrades studieren. 

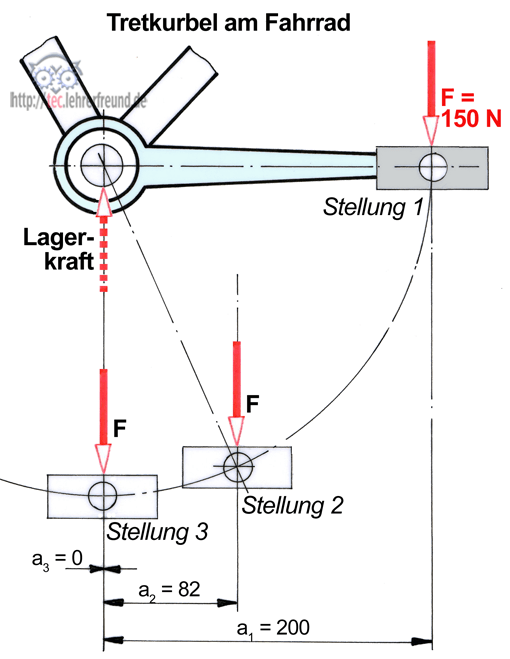
Aufgaben
a) Berechnen Sie die Drehmomente für die drei skizzierten Stellungen.
Lösung:
Stellung 1: M1 = 30 Nm
Stellung 2: M2 = 12,3 Nm
Stellung 3: M3 = 0 Nm

b) Wie groß ist die Lagerkraft F_L?
Lösung: F_L = F = 150 N

c)  Stellung 1: Wie ändert sich die Drehkraftwirkung auf die Kurbelwelle, wenn mit dem Fuß unter einem Winkel von 45° getreten wird?
Lösung: Hebelarm (zeichnerisch ermittelt) 141 mm. M = 21,15 Nm

In Zusammenhang mit Kräftepaaren betrachten wir die Kräfteverhältnisse an der Lagerung eines Fahrrad-Tretlagers. 
Weil der Fall komplizierter ist als man denkt, wollen wir ihn etwas vereinfachen.
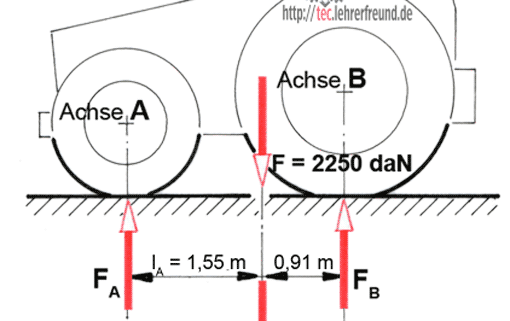
Auf das Tretlager wirken zwei äußere Kräfte, die Pedalkraft F_P und die Kettenkraft F_K (siehe auch Fahrradantrieb). Da diese Kräfte im skizzierten Fall einen rechten Winkel zueinander bilden, ergeben sich aus der Resultierenden F_P,K die Lagerstützkräfte F_A und F_B. 

Der axiale Abstand c zwischen F_P und F_K ist gering im Verhältnis zu den Lagerabständen a und b. Wir vereinfachen den Fall, indem wir den Abstand zwischen Kurbel und Kettenrad vernachlässigen und davon ausgehen, dass F_P und F_K auf derselben Ebene angreifen. Dafür könnte man die Mitte zwischen F_P und F_K annehmen.

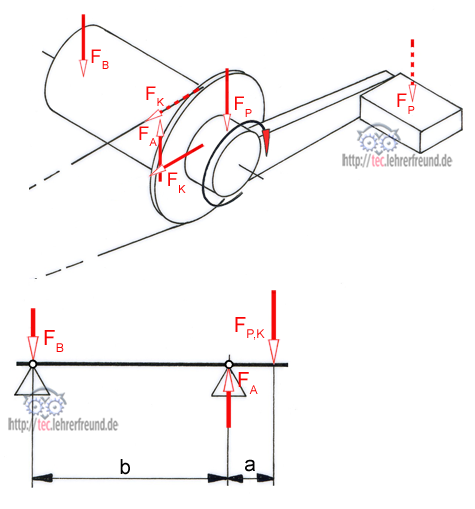
Daraus ergibt sich eine unkomplizierte Berechnung der Lagerkräfte: Man legt den Drehpunkt z. B. in das Lager B. Dann ist
          M _links = M _rechts
           F_A • b = F_P,K • (a + b)
                 F_A = F_P,K • (a + b) : b 

Nicht geklärt werden in dieser Rechnung die Richtungen von F_A und F_B. 

______________________ 

Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.