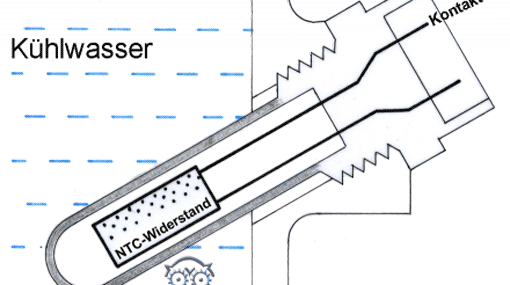
Wärmeausdehnung 08.06.2015, 06:11

Die meisten in technischen Einrichtungen verwendeten Stoffe (z.B. Stahl, Messing, Luft, Hydrauliköl, Quecksilber) dehnen sich bei Erwärmung in alle Richtungen gleichmäßig aus; bei Abkühlung ziehen sie sich wieder zusammen. Die Längenänderung eines bestimmten Stoffes berechnet man mit dem Längenausdehnungskoeffizienten α. Mit Rechenaufgaben.

Wärmeausdehnung

Die meisten in technischen Einrichtungen verwendeten Stoffe (z.B. Stahl, Messing, Luft, Hydrauliköl, Quecksilber) dehnen sich bei Erwärmung in alle Richtungen gleichmäßig aus; bei Abkühlung ziehen sie sich wieder zusammen. Diese Eigenschaft kann störend sein, z. B. bei Eisenbahnschienen und Brücken, die sich in der Hitze verformen. Man kann sich die Verformung auch zunutze machen, etwa für Temperaturmessungen oder beim Einbau von Wälzlagern. 
Messungen im Maschinenbau erfordern zur Vermeidung von Messfehlern eine konstante Umgebungstemperatur. Sie wurde auf 20°C festgelegt und heißt »Bezugstemperatur«.

Die thermische Ausdehnung eines Körpers hängt ab  
– von seinem Werkstoff 
– der Temperaturdifferenz  
– von seiner Länge bzw. seinem Volumen. 

Im Allgemeinen hat der Längenausdehnungskoeffizient eine positive Größe. Auch gibt es Materialien (z.B. einige Arten von Glaskeramik), deren Wärmeausdehnungskoeffizient nahezu Null ist. Manche Stoffe zeigen in einem bestimmten Temperaturbereich ein ungewöhnliches Verhalten (z.B. Wasser zwischen 0 und 4°C = Anomalie des Wassers). 

Die Längenänderung eines bestimmten Stoffes berechnet man mit dem Längenausdehnungskoeffizienten α. Er gibt an, um welchen Betrag Δl im Verhältnis zu gesamten Länge l₀ sich ein fester Körper bei einer Temperaturänderung von 1 Kelvin vergrößert oder verkleinert. So ist der Längenausdehnungskoeffizient α von Eisen 11,8 • 10⁻³ K⁻¹     

Formelzeichen

l₀     Anfangslänge    in m 
Δl    Verlängerung     in m 
α      Längenausdehnungskoeffizient    in K⁻¹

Bei gleichmäßiger Erwärmung oder Abkühlung um die Temperaturdifferenz ΔT erhält man die Längenänderung Δl eines Stabs, wenn man den Längenausdehnungskoeffizient α des Stabmaterials mit der Stablänge l₀ und der Temperaturdifferenz ΔT multipliziert:

Δl = α • l₀ • ΔT 

l₀ = Δl : (α • ΔT)

ΔT = Δl : (α • l₀)

Anmerkung zur Temperatureinheit Kelvin: 
Das Kelvin (Einheitenzeichen: K) ist die SI-Basiseinheit der thermodynamischen Temperatur und zugleich gesetzliche Temperatureinheit. In Deutschland, Österreich, der Schweiz sowie in anderen europäischen Ländern gilt auch das Grad Celsius (Einheitenzeichen: °C) als gesetzliche Einheit für die Angabe von Celsius-Temperaturen und deren Differenzen. Dabei entspricht 0 °C umgerechnet 273 K. Die Skizze zeigt den Zusammenhang zwischen °C und K. 

Hier die Längenausdehnungskoeffizienten α in 10^–6 K^–1 einiger Metalle: 

Al    23,1 
Cr     4,9
Cu  16,5
Fe   11,8
Pb   28,9 
Zn   30,2 

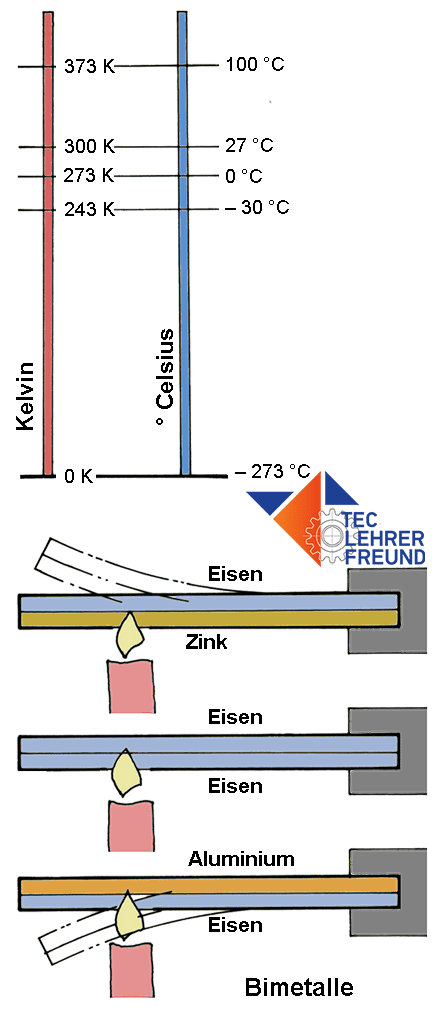
Bild oben: Beim Erwärmen zweier fest aneinander haftender Metalle bewirkt das Metall mit dem größeren Längenausdehnungskoeffizient (Al, Zn) eine Krümmung des Metallstreifens hin zum Metall mit dem kleineren Längenausdehnungskoeffizient (Fe).

Aufgaben 

1. Zwischen 10 m langen Eisenbahnschienen bleibt ein Abstand von 6 mm. Bei welcher Temperaturdifferenz stoßen die Schienenenden aufeinander? (α = 14 • 10^-6 K^-1). Zu beachten: Weil sich auch die benachbarten Schienen ausdehnen, wird für eine Schiene nur Δl/2 gerechnet.

2. Zwischen je 30 m langen Eisenbahnschienen wurden Stoßfugen gelassen. Bei Erwärmung von 10°C auf 25°C verengt sich diese um 35% ihres Anfangswertes (α = 14 • 10_-6 K^-1).
a) Bei welcher Temperatur stoßen die Schienen aufeinander?
b) Wie groß ist der anfängliche Abstand?

    
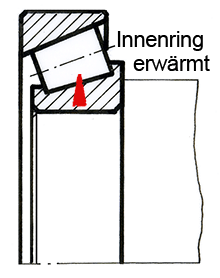
3. Der Innenring eines Kegelrollenlagers mit einem Bohrungsdurchmesser von 100 mm wird auf eine Welle montiert. Dazu wird der Ring von 20 °C auf 100 °C erwärmt (α = 14 • 10^-6 K^-1), so dass er sich leicht auf die Welle schieben lässt.

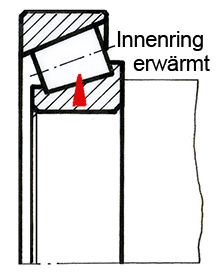
a) Um wieviel mm dehnt sich die Bohrung bei der Erwärmung? 

b) Die Bohrung soll sich um 0,15 mm dehnen. Auf welche Temperatur muss man den Innenring erwärmen? 

4. Ein Stab ist bei 20 °C 298 mm lang. Wird er auf 47 °C erwärmt, dehnt er sich um 0,186 mm aus. Der Längenausdehnungskoeffizient des Stabwerkstoffs ist zu berechnen.

Lösungsvorschläge

Aufgabe 1, Eisenbahnschienen: 

ΔT = Δl : (α • l₀) = 3 • 10^–3 m : (14 • 10^-6 K^-1 • 10 m)

ΔT = 21,43 K 

Hinweis: Im modernen Gleisbau verlegt man Schienen ohne Stoß. Die Festigkeit der Schienen und Schwellen ist in der Lage, die Kraft, die durch die Längenänderung entsteht, aufzufangen.

Aufgabe 2, Eisenbahnschienen: 

ΔT = t1 – t2 = 25°C – 10 °C = 15 °C = 15 K

a)  Bei welcher Temperatur stoßen die Schienen aufeinander? Da die Längenänderung proportional zur Temperaturerhöhung ist, kann man schreiben:

(ΔT1≜ 35%; ΔT2 ≜ 100%) ➔ ΔT1 : 35% = ΔT2 : 100% 

ΔT2 = ΔT1 : 35% • 100% = 15 K : 35% • 100% = 42,86 K 

ΔT2 = 42,86 K Bei dieser Temperaturerhöhung stoßen die Schienenenden aufeinander. 

Bei Erwärmung verlängert sich die 30 m lange Schiene nach beiden Seiten. Zum Schließen der Lücke ist nur die halbe Ausdehnung nötig; die andere Hälfte kommt von der Nachbarschiene. 

Δl = α • l₀ • ΔT = 30 m • 14 • 10^-6 K^-1 • 42,86 K = 

Δl = 0,018 m = 18 mm, d.h. vor der Erwärmung war der Stoß 18 mm breit. 

Aufgabe 3, Kegelrollenlager: 

a) Die 100 mm-Bohrung dehnt sich um 

Δl = α • l₀ • ΔT  = 14 • 10^-6 K^-1 • 0,1 m • 80 K = 

Δl = 0,000112 m = 0,112 mm 

b) Für eine Dehnung von 0,15 mm ist erforderlich: 
ΔT = Δl : (α • l₀) = 0,00015 m : (14 • 10^-6 K^-1 • 0,1 m) = 

ΔT = 107,14 K 

Aufgabe 4, Stab: 

α = ​Δl : ( l₀ • ΔT) = 0,000 186 m : (0,298 m • 27 K) =

α = ​23,1 • 10^–6 / K 
Es handelt sich also um einen Stab aus Aluminium.