Fahrrad: Kräfte und Drehmomente am Pedal 29.12.2012, 06:25

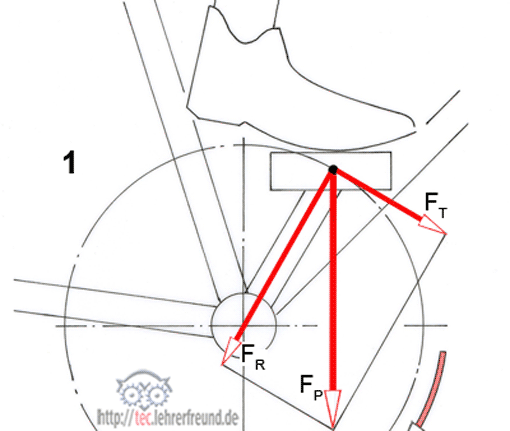
Beim Fahren übt der Fuß eine Kraft auf das Pedal aus, die, sofern ein wirksamer Hebelarm vorhanden ist, von der Tretlagerwelle in ein Drehmoment umgewandelt wird. Doch: Wirken alle Kräfte am Pedal gleichermaßen?

Kräfte und Drehmomente am Pedal

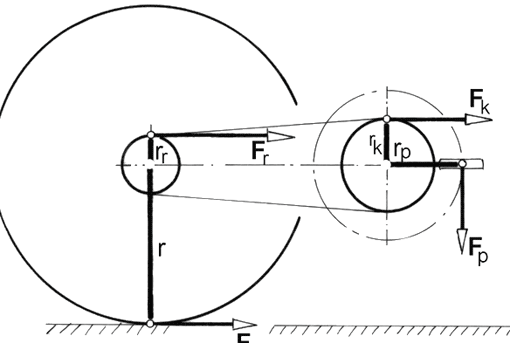
Bilder 1 und 2:
Beim Treten übt der Fuß eine Kraft F_P auf das Pedal aus, die, sofern ein wirksamer Hebelarm vorhanden ist, von der Tretlagerwelle in ein Drehmoment umgewandelt wird. Das Drehmoment steht auch am Zahnkranz und an der Kette zur Verfügung.
Die Drehwirkung ist umso größer, je größer die Tretkraft F_P und je länger der Hebelarm ist. Das Produkt aus Kraft und Hebelarm nennt man Drehmoment: M = F_P • l₁; es wird in der Einheit Nm gemessen. Der wirksame Hebelarm ist immer der senkrechte Abstand zwischen der Wirkungslinie der Kraft und dem Drehmittelpunkt der Tretlagerwelle.
Sieht man sich das Kräfteparallelogramm mit den Kräften F_P, F_R und F_T an (Bild 1), erkennt man, dass durchgängig nur F_T dem Vorwärtsfahren zugute kommt. Der zur Lagermitte hin gerichtete Kraftanteil F_R bleibt für das Fahren wirkungslos, denn er erzeugt an der Tretlagerwelle kein Drehmoment. Er belastet nur das Lager. 
F_T = Tangenzialkraft; F_R Lagerkraft.

Im Bild 2 sind drei Tretpositionen eingezeichnet:
- Pedalstellung a: Im oberen Totpunkt ist das Drehmoment Null, weil F_P durch die Lagermitte geht und deshalb kein Kraftarm vorhanden ist.

- Pedalstellung b: Der senkrechte Abstand von der Wirkungslinie der Pedalkraft F_P zum Drehpunkt ist l₁ = sin α • R. Im Tretlager wirkt das Drehmoment M = F_P • l₁. Dieselbe Wirkung ergibt sich aus F_T • R, weil R und F_T einen rechten Winkel miteinander bilden.

- Pedalstellung c: M = F_P • R. 

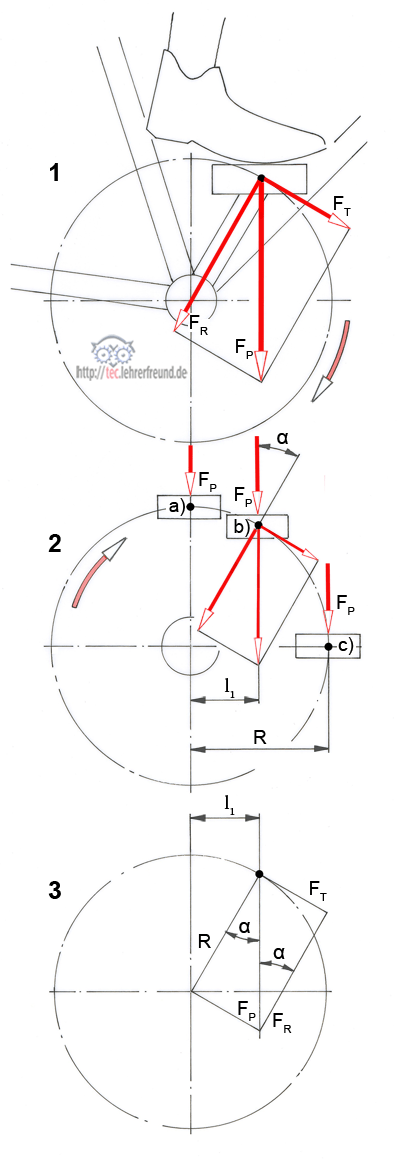
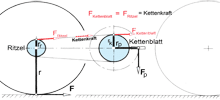
Bild 3: Kräfte- und Hebelverhältnisse am Pedal. 

sin α = F_T : F_P = l₁ : R

cos α = F_R : F_P –> F_P = F_R : cos α 

M = F_T • R = F_P • l₁

l₁ = sin α • R 

Berechnungsbeispiele:

1. An einer 170 mm langen Tretkurbel wirkt eine senkrechte Tretkraft von 180 N. Welches Drehmoment wird in der Tretlagerwelle erzeugt? 

2. Eine Pedalkraft F_P = 160 N wirkt auf ein Pedal (Kurbellänge 170 mm), das in der Stellung 30° nach OT (oberer Totpunkt) steht. 

a) Wie groß ist das Drehmoment in der Tretlagerwelle? 
b) Berechnen Sie den wirksamen Hebelarm. 
c) Welche Kraft F_R wirkt auf das Tretlager?  

Lösungsvorschläge:

1. M = F_P • l₁ = 180 N • 0,17 m = 30,6 Nm

2.
a) M = F_P • sin α • R = 160 N • 0,5 • 0,17 m = 13,6 Nm 
b) l₁ = R • sin α = 170 mm • 0,5 = 85 mm 
c) F_R = F_P • cos α = 160 N • 0,866 = 138,6 N