Allgemeines Kräftesystem: Rechnerische Gleichgewichtsbedingungen (1) 13.01.2012, 08:17
Ein Körper ist dann im Gleichgewicht, wenn die algebraische Summe sämtlicher x- und y-Komponenten gleich Null ist und wenn die algebraische Summe sämtlicher Momente für jeden beliebigen Drehpunkt ebenfalls gleich Null ist. Berechnung eines Falls aus der Praxis.
Beachten: Niveau Techn. Gymnasium, Berufskolleg u. Ä.
Wir beziehen uns hier auch auf die Erörterungen im tec.LEHRERFREUND-Beitrag »Zentrale Kräftesysteme: Zeichnerische und rechnerische Lösungsansätze (1)«
Beschäftigen wir uns mit einem allgemeinen Kräftesystem, um unbekannte Kräfte zu ermitteln, dann zerlegen wir die angreifenden Kräfte als erstes in x- und y-Komponenten. Dabei dürfen wir keine Kraft vergessen, denn sonst wird die Lösung unweigerlich falsch. Gegen ein solches Missgeschick können wir uns schützen, wenn wir eine Lageskizze des freigemachten Bauteils zeichnen. Auf ihrer Grundlage schreiben wir die Gleichgewichtsbedingungen auf und berechnen dann die unbekannten Kräfte.
Das Achsenkreuz des Systems legen wir sinnvollerweise so, dass möglichst wenige Kräfte in Komponenten zerlegt werden müssen. Im Normalfall liegt die x-Achse waagrecht und die y-Achse senkrecht; dies muss jedoch nicht unbedingt so sein. Es ist manchmal sogar zweckmäßiger, eine andere Lage des rechtwinkligen Achsenkreuzes zu wählen.
Ein Körper ist dann im Gleichgewicht, wenn die algebraische Summe sämtlicher x- und y-Komponenten gleich Null ist und wenn die algebraische Summe sämtlicher Momente für jeden beliebigen Drehpunkt ebenfalls gleich Null ist.
Die rechnerischen Gleichgewichtsbedingungen lauten:
I. ∑Fx (Summe aller Kräfte in x-Richtung) = 0
II. ∑Fy (Summe aller Kräfte in y-Richtung) = 0
III. ∑M (Summe aller Momente um einen beliebigen Drehpunkt) = 0
(siehe auch tec.LEHRERFREUND-Beitrag »Zentrale Kräftesysteme: Zeichnerische und rechnerische Lösungsansätze (1)«).
Aus diesen drei Gleichungen berechnen wir die unbekannten Kräfte. Reichen sie dazu nicht aus, ist der Körper statisch unbestimmt. Die Berechnung erfordert dann Verfahren, die nicht Gegenstand der tec.LEHRERFREUND-Beiträge sind.
Die oben beschriebenen Erläuterungen wollen wir auf ein praktisches Beispiel übertragen.
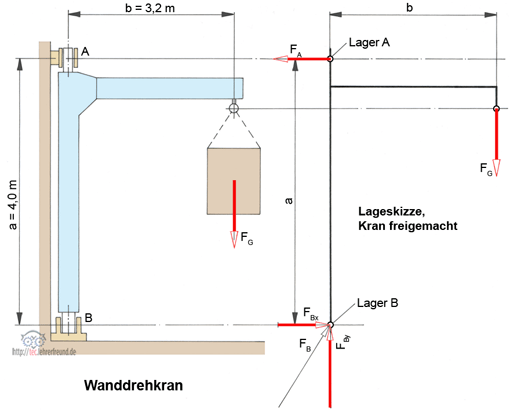
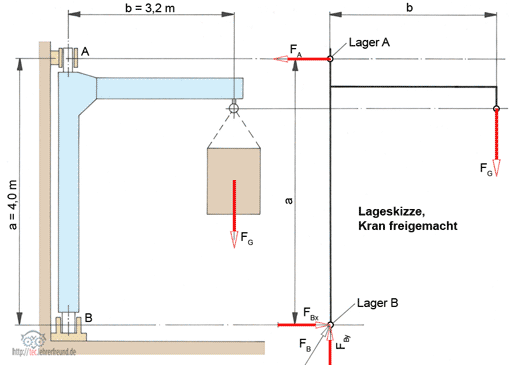
Für den Wanddrehkran im Bild sind die Lagerkräfte FA und FB zu berechnen.
In der Lageskizze des freigemachten Körpers finden wir die Kräfte:
- Hubgewicht FG = 2500 daN, Wirklinie bekannt;
- Halslagerkraft FA, Größe unbekannt, Wirklinie bekannt –> waagerecht wegen des einwertigen Lagers;
- Stützlagerkraft FB; ihre Größe ist ebenso wie die Wirklinie unbekannt. Wir tragen deshalb die Wirklinien der Komponenten FBx und FBy ein.
Die Aufgabenlösung finden Sie im Beitrag »Allgemeines Kräftesystem: Rechnerische Gleichgewichtsbedingungen (2)«