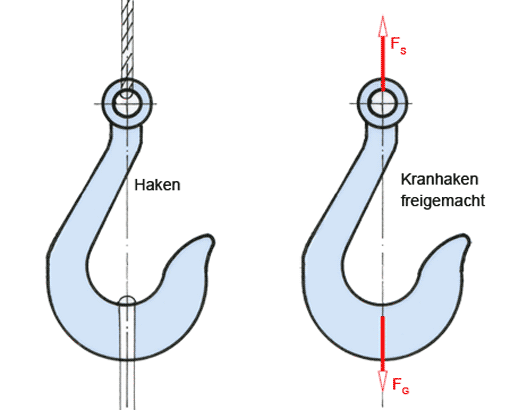
Zentrale Kräftesysteme: Zeichnerische und rechnerische Lösungsansätze (2) 10.01.2012, 08:07

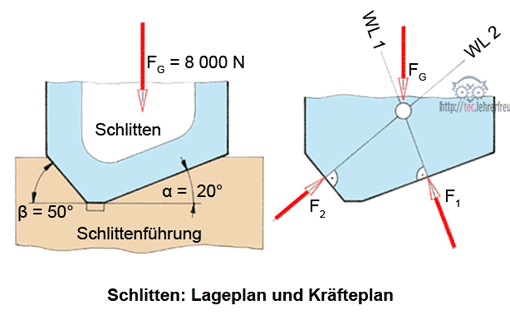
Am Beispiel einer Schlittenführung zeigen wir, wie man in einem zentralen Kräftesystem unbekannte Kräfte rechnerisch und zeichnerisch ermittelt. In der Kräfteberechnung spielen die Gleichgewichtsbedingungen die zentrale Rolle.

Fortsetzung des Beitrags Zentrale Kräftesysteme: Zeichnerische und rechnerische Lösungsansätze (1)

Wenn Körper im Gleichgewicht sind 

Jeder ruhende Körper ist im Gleichgewicht. Dies setzt voraus, dass alle Bewegungsursachen - Kräfte und Drehmomente - gesperrt sind. 

Im zentralen Kräftesystem herrscht Gleichgewicht, wenn keine Verschiebung möglich ist, d. h. wenn alle am Körper angreifenden Kräfte in x- und y-Richtung sich aufheben. Daraus ergeben sich die beiden Gleichgewichtsbedingungen:

I. ∑F_x (Summe aller Kräfte in x-Richtung) = 0

II. ∑F_y (Summe aller Kräfte in y-Richtung) = 0 

Wirken an einem Körper darüber hinaus Drehmomente, dann herrscht Gleichgewicht, wenn sich auch die Drehmomente aufheben. Daraus ergibt sich die 3. Gleichgewichtsbedingung: 

III. ∑M (Summe aller Momente um einen beliebigen Drehpunkt) = 0

2. Schlittenführung: Rechnerische Lösung 

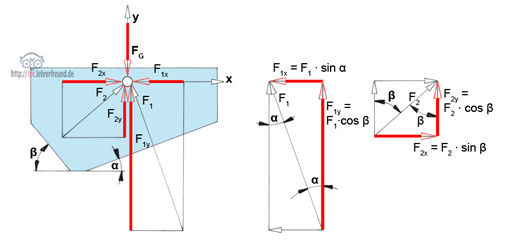
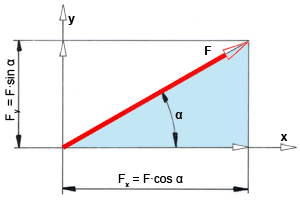
Allgemein gilt: Bei einer unter dem Winkel α geneigten Kraft F sind deren Komponenten
F_x = F · cos α und
F_y = F · sin α
(Skizze) 

In diesem Beispiel wirken keine Drehmomente.

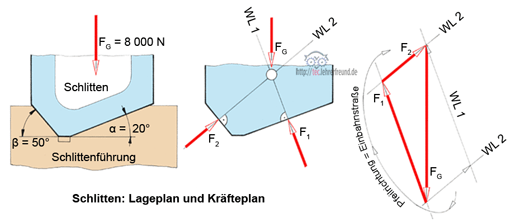
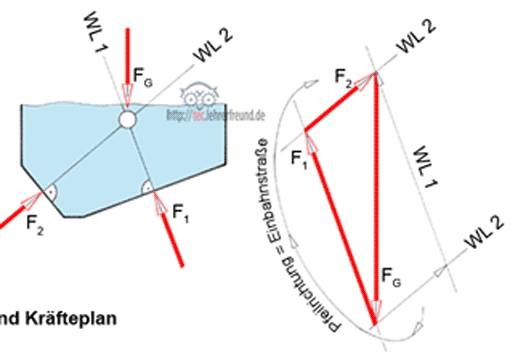
Wir machen eine Lageskizze (Zeichnung unten), in die wir alle Kräfte des freigemachten Schlittens eintragen. Diese zeichnen wir immer als senkrecht aufeinander stehende Komponenten, wenn die Kräfte selbst nicht in die Richtungen der x- bzw. y-Achse fallen. Im Beispiel der Schlittenführung erscheinen an der Stelle von F₁ und F₂ die Komponenten F_1x, F_1y, F_2x und F_2y. 
Aus den Zerlegungsparallelogrammen ergibt sich:
F_1x = F₁ · sin α
F_1y = F₁ · cos α
F_2x = F₂ · sin β
F_2y = F₂ · cos β

Ausgehend von den rechnerischen Gleichgewichtsbedingungen beim zentralen Kräftesystem lässt sich für den Schlitten  feststellen:
I. ∑F_x = 0 = + F_2x - F_1x
II. ∑F_y = 0 = - F_G + F_2y + F_1y
oder
I. ∑F_x = 0 = + F₂ · sin β - F₁ · sin α
II. ∑F_y = 0 = - F_G + F₂ · cos β + F₁ · cos α

Die Lösung vereinfacht sich, wenn wir die schon bekannten Winkelfunktionswerte sofort einsetzen. Vom Taschenrechner lesen wir ab: 
sin α = sin 20° = 0,342;
cos α = cos 20° = sin 70° = 0,94
sin ß = sin 50° = 0,766;
cos ß = cos 50° = sin 40° = 0,643.
Werden diese Werte in die Gleichgewichtsbedingungen eingesetzt, dann ergibt sich: 
I. ∑F_x = 0 = + 0,766 · F₂  - 0,342 · F₁,
II. ∑F_y = 0 = - F_G + 0,643 F₂ + 0,94 · F₁ .

Das sind zwei Gleichungen mit zwei Unbekannten, die nach den Verfahren der Gleichungslehre gelöst werden können, z. B. mit Hilfe des Einsetzungsverfahrens:  Aus Gleichung I. findet man:  
F₂ =  0,342 : 0,766 · F₁ = 0,447 · F₁
Dies setzen wir für F₂ in Gleichung II. ein: 
II. ∑F_y = 0 = - F_G + 0,643 · 0,447 · F₁ + 0,94 · F₁ .
Jetzt haben wir eine Gleichung mit einer Unbekannten (F₁), die wir nach F₁ auflösen: 
0,287 · F₁ + 0,94 F₁ = F_G
                  1,227 · F₁ = F_G
F₁ = 8000 N : 1,227 = 6 520 N

Aus der Gleichung I. ergibt sich:
F₂ = 0,447 · F₁ = 0,447 · 6520 N = 2920 N

Die rechnerischen Ergebnisse vergleichen wir schließlich mit den zeichnerischen Ergebnissen.