Formeln umstellen (2): Übungen 01.04.2010, 15:38

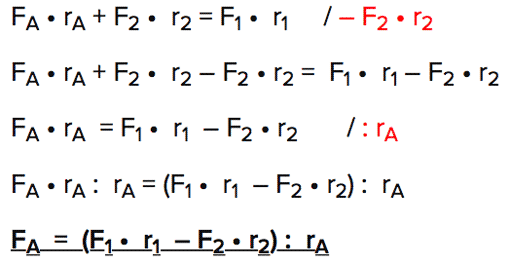
Vertiefende Übungen zum Thema »Formeln umstellen«

Formeln aus der Technik umstellen: Übungen

Fortsetzung des Beitrags Formeln umstellen (1). In diesem Beitrag wird das Thema vertieft. Für die einfacheren Aufgaben 1. bis 3. geben wir nur die Lösungen an, die weiteren Aufgaben rechnen wir schrittweise durch.

1. Riementrieb (siehe Skizze in Formeln umstellen (1))

d₁• n₁ = d₂ • n₂

Aufgabe:

a) Stellen Sie die Formel nach allen vier Größen um

b) Das Übersetzungsverhältnis des Riementriebs ist i = n₁: n₂. Welche weitere Möglichkeit ergibt sich aus der Formel, i zu berechnen?

2. Dreiecksfläche (siehe Skizze in Formeln umstellen (1))

A = 64 cm², h = 9 cm. Stellen Sie die Flächenformel um und berechnen Sie g.

3. Stirnrad, Zahnrad-Außendurchmesser: d_a = z • (m + 2) (siehe Skizze in Formeln umstellen (1))

a) Stellen Sie die Formel um nach m

b) Stellen Sie die Formel um nach z

4. Lagerkräfte

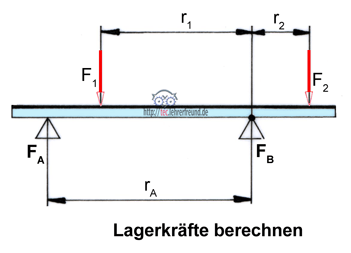
a) Nehmen Sie den Drehpunkt bei F_B an und schreiben Sie die Momentengleichung.

b) Stellen Sie die Momentengleichung nach F_A um

c) Stellen Sie die Momentengleichung nach r_A um

d) Berechnen Sie r_A, wenn gegeben ist F_A = 800 N, F₁ = 1 200 N, F₂ = 400 N, r₁ = 0,5 m, r₂ = 0,2 m.

5. Kommt in einer Formel die gesuchte Größe mehrfach vor, dann wird das Umstellen aufwändig.

Beispiel Widerstand einer Parallelschaltung mit 2 Einzelwiderständen R₁ und R₂.

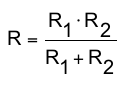
a) Die Formel soll nach R₁ umgestellt werden.

b) R = 52 mΩ, R₂ = 90 mΩ. Berechnen Sie R₁.
 

Lösungen

1. a)

d₁ = d₂ • n₂ / n₁

d₂ = d₁ • n₁ / n₂

n₁ = d₂ • n₂  / d₁

n₂ = d₁ • n₁ / d₂

1. b)      i = d₂/d₁

2. Grundlinie g = 14,22 cm

3. a) m = (d_a : z) – 2      b) z = d_a : (m + 2)  

4. a)

Summe der rechtsdrehenden Momente = Summe der linksdrehenden Momente

ΣM_rechts =  ΣM_links   (Σ = sigma = Symbol für Summe)

F_A • r_A + F₂ •  r₂ =  F₁ •  r₁

4. b)

F_A • r_A + F₂ •  r₂ = F₁ •  r₁     / – F₂ • r₂

F_A • r_A + F₂ •  r₂ – F₂ • r₂ =  F₁ •  r₁ – F₂ • r₂

F_A • r_A  = F₁ •  r₁  – F₂ • r₂       / : r_A

F_A • r_A :  r_A = (F₁ •  r₁  – F₂ • r₂) :  r_A

F_A  =  (F₁ •  r₁  – F₂ • r₂) :  r_A

4. c)

Aus der Gleichung F_A  =  (F₁ •  r₁  – F₂ • r₂) :  r_A ergibt sich nach Umstellung:

r_A  =  (F₁ •  r₁  – F₂ • r₂) :  F_A

4. d)  

In 4. c) Zahlen eingesetzt und berechnet: r_A = 0,65 m

5.
a)

Ausklammern: Die rechte Seite R₁ · R₂ – R · R₁ enthält zwei Mal den Wert R₁. Der Ausdruck lässt sich durch Ausklammern dieses Werts so vereinfachen, dass R₁ - wie gewünscht - nur noch einmal erscheint: R₁ · (R₂ – R).

5. b) R₁ = 0,123 Ω  = 123 mΩ

Zu beachten in der Parallelschaltung von Widerständen:
- Die Zahlenwerte für R, R₁ usw. müssen in Ohm eingesetzt werden!
- Der Gesamtwiderstand R einer Parallelschaltung ist kleiner als der kleinste Einzelwiderstand