Kräfte: Unbekannte Kräfte zeichnerisch ermitteln (2) 07.10.2011, 11:42
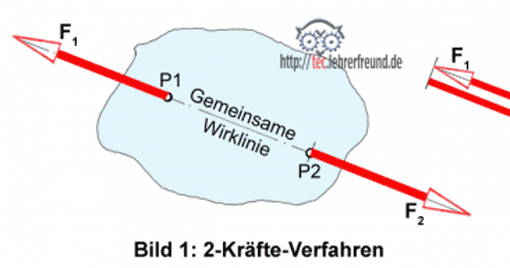
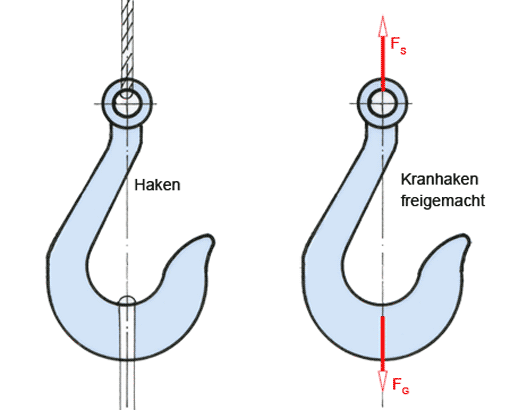
Aufgaben mit 3-Kräfte-Gleichgewicht sind häufig zu lösen. Beim Gleichgewicht von vier nicht parallelen Kräften bedient man sich der Culmannschen Geraden. Sie geht von der Überlegung aus, dass Gleichgewicht im System nur vorhanden ist, wenn die Resultierenden von je zwei Kräften auf derselben Wirklinie liegen und gegeneinander wirken.
Fortsetzung des Beitrags »Unbekannte Kräfte zeichnerisch ermitteln (1)«
Lernniveau: Technische Oberschule, Berufskolleg u. Ä.
3. Vier-Kräfte-Verfahren (Gleichgewicht von 4 nicht parallelen Kräften)
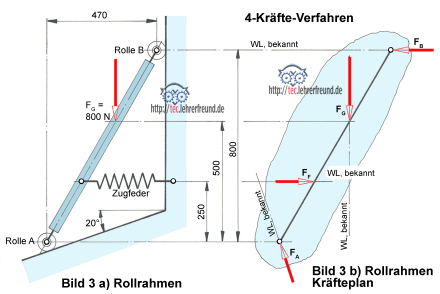
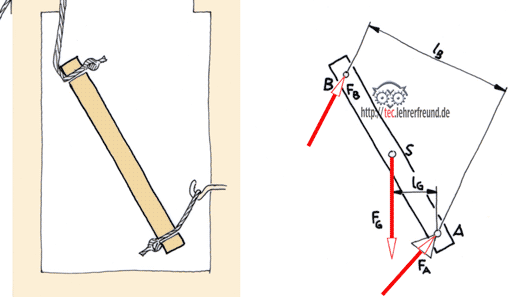
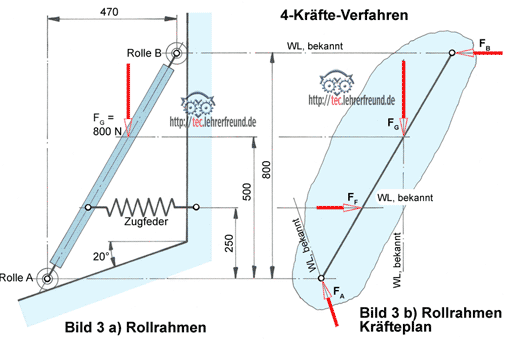
Der Rollrahmen in Bild 3 a) liegt an den Rollen A und B reibungsfrei auf, so dass er unter der Belastung FG verschoben würde, wenn nicht die Zugfeder mit einer Federkraft FF das Gleichgewicht hielte.
Aufgabe:
Die Federkraft FF soll zeichnerisch bestimmt werden, ebenso die Stützkräfte FA und FB.
Bild 3 b) zeigt die Kräfte:
- Last FG, Größe gegeben mit 80 N, Wirklinie bekannt;
- Lagerkraft FA, Größe unbekannt, Wirklinie bekannt (einwertige Lagerstelle) ;
- Lagerkraft FB, Größe unbekannt, Wirklinie bekannt (einwertige Lagerstelle);
- Federzugkraft FF, Größe unbekannt, Wirklinie bekannt (Feder überträgt nur in Zugrichtung Kräfte).
Es wirken demnach am Körper 4 Kräfte, deren Wirklinien bekannt sind. Eine Kraft (Last FG) ist auch nach Größe und Richtung bekannt.
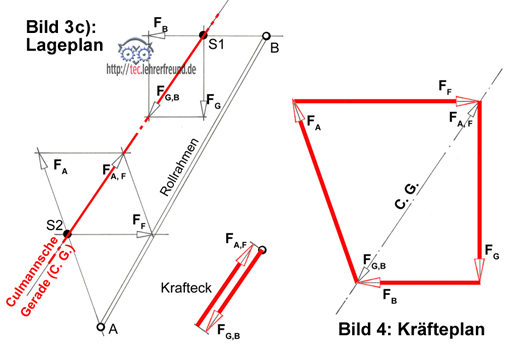
Fassen wir nun wieder (wie beim 3-Kräfte-Verfahren) gedanklich je 2 Kräfte zu einer Resultierenden zusammen (Bild 3 c), z. B. die Kräfte FA und FF zu FA,F und die Kräfte FB und FG zu FG,B, dann haben wir es wiederum mit nur 2 Kräften zu tun. Diese beiden Resultierenden können nur im Gleichgewicht sein, wenn sie eine gemeinsame Wirklinie haben. Das muss nach Bild 3 c) die Verbindungslinie der Schnittpunkte je zweier Kräfte sein; diese Verbindungslinie ist als »Culmannsche Gerade« bekannt. Die auf der gemeinsamen Culmannschen Geraden liegenden Resultierenden müssen natürlich ein geschlossenes Krafteck ergeben (Bild 3 c).
Es gilt also:
Vier nicht parallele Kräfte sind im Gleichgewicht, wenn die Resultierenden je zweier Kräfte ein geschlossenes Krafteck bilden und eine gemeinsame Wirklinie — die Culmannsche Gerade — haben (4-Kräfte-Verfahren).
Wir lösen nun die Aufgabe, indem wir den Lageplan zeichnen (Bild 3c) und dort die Wirklinien je zweier Kräfte zum Schnitt bringen. Punkt S1 ist der Schnittpunkt der Kräfte FB und FG, Schnittpunkt S2 der von FA und FF. Damit ist die Culmannsche Gerade gefunden, und der Kräfteplan (Bild 4) kann gezeichnet werden.
Wir legen uns dazu die gegebene Kraft FG maßstäblich hin, übertragen die Culmannsche Gerade vom Lage- in den Kräfteplan, lassen sie durch Anfangspunkt von FG laufen und schließen dieses Krafteck durch die zugehörige Kraft FB. Das Krafteck zeigt die Kräfte FG , FB und FG,B. In gleicher Weise können wir nun das andere Krafteck zeichnen mit den Kräften FA, FF und FA,F. Den Richtungssinn der Kräfte finden wir aus der Bedingung des »geschlossenen Kräftezuges«, d. h. der Umfahrungssinn des Kraftecks muss, von FG ausgehend, beibehalten werden.
Arbeitsplan:
- Lageplan zeichnen mit freigemachtem Körper und damit die Wirklinien der Belastungen und Lagerkräfte festlegen (Bild 3b);
- Wirklinien je zweier Kräfte zum Schnitt bringen;
- Gefundene Schnittpunkte verbinden zur Wirkungslinie der beiden Resultierenden (= Culmannsche Gerade);
- Kräfteplan (Bild 4) mit nach Größe und Richtung bekannter Kraft anfangen;
- Kräfteplan mit Culmannscher Geraden und den Wirklinien der anderen Kräfte schließen;
- Beachten: Die Kräfte eines Schnittpunkts im Lageplan ergeben ein Teildreieck im Kräfteplan.
________________________
Das Drei- und Vier-Kräfte-Verfahren werden wir später an verschiedenen praktischen Beispielen ausprobieren:
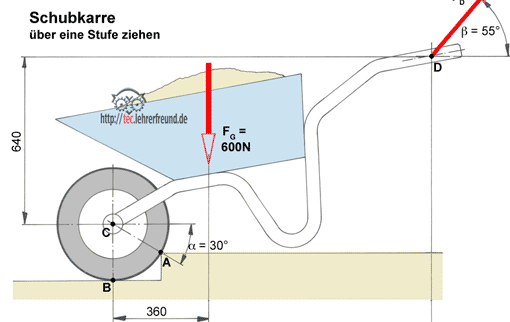
- Schubkarre
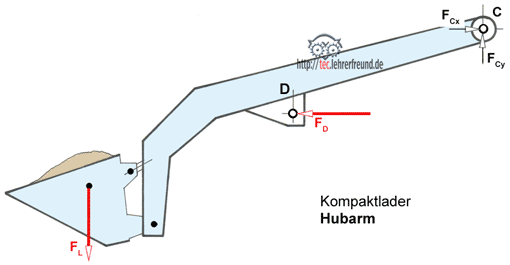
- Kompaktlader
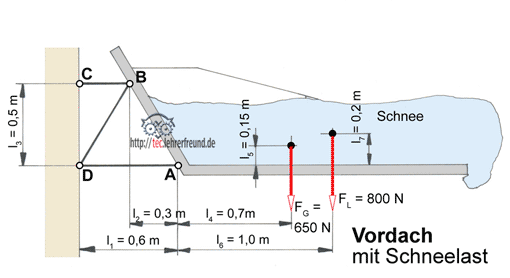
- Vordach
- Mountainbike