Kräfte an einer Backenbremse 11.10.2011, 13:21
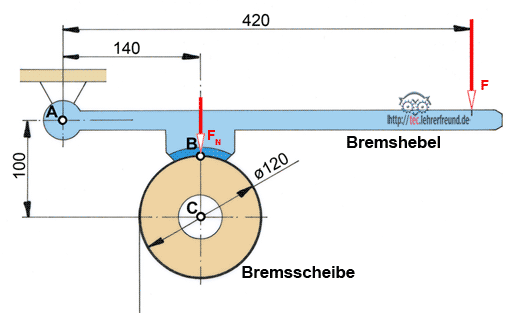
In einem vorangegangenen Beitrag wurde das Gleichgewicht von drei an einem Bauteil angreifenden Kräften behandelt. Dies vertiefen wir am Beispiel einer Backenbremse.
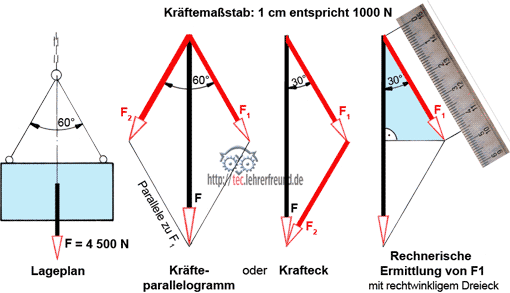
Kräfte an einer Backenbremse
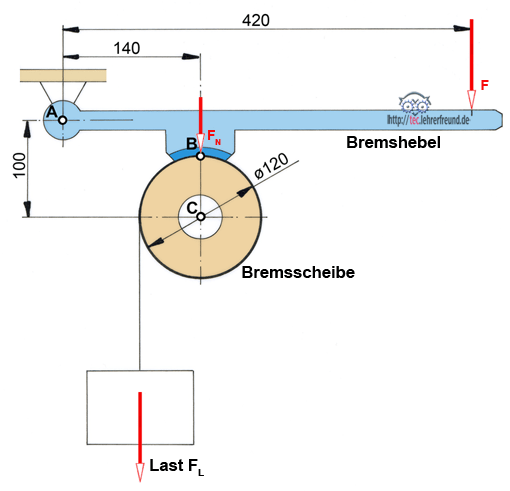
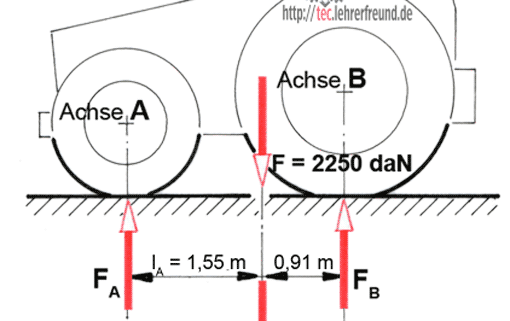
Durch Druck auf den Bremshebel (Kraft F) wird die Bremsscheibe in Ruhe gehalten. Der Bremshebel ist im Punkt A gelagert. Die vom Bremshebel auf die Bremsscheibe wirkende Kraft ist FN. Die Last FL = 850 N versucht, die Bremsscheibe in Drehung zu versetzen. Die Reibzahl µ ist 0,45.
Informationen zum Thema »Reibung« finden Sie in tec.LEHRERFREUND-Beiträgen.
Folgende Aufgaben sind zu lösen:
1. Machen Sie die Bremsscheibe frei.
2. Berechnen Sie FN.
3. Berechnen Sie FC und die Richtung in der sie wirkt.
4. Machen Sie den Bremshebel frei.
5. Ermitteln Sie zeichnerisch die Kräfte F und FA.
Lösungsvorschläge:
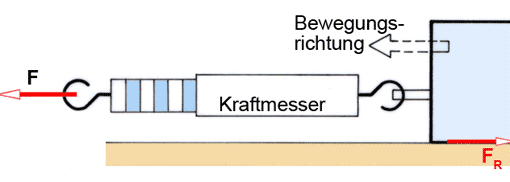
1. Bremsscheibe freimachen, siehe Skizze
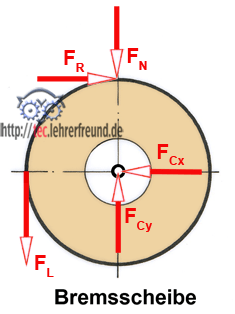
Freimachen bedeutet: Man nimmt vom betrachteten Teil (hier der Bremsscheibe) alle Nachbarteile weg. Dafür werden alle Kräfte eingetragen, die auf die Scheibe von außen wirken.
2. FN berechnen.
Die Reibkraft FR ist immer kleiner als die Normalkraft FN.
µ = FR : FN –>
FN = FR : µ; FR ist gleich groß wie FL = 850 N.
FN = 850 N : 0,45 = 1889 N
3. Die Größe von FC berechnen und die Richtung, in der sie wirkt.
Größe und Richtung von FC sind nicht bekannt. Man berechnet sie über die Komponenten FCx und FCy. Aus der freigemachten Bremsscheibe ergibt sich:
∑Fx = 0 = FCx – FR →
FCx = FR = 850 N
∑Fy = 0 = FCy – FN – FL →
FCy = FN + FL = 1889 N + 850 N = 2739 N
Pythagoras: FC2 = FCx2 + FCy2 → FC = √ FCx2 + FCy2 = √ (850 N)2 + (2739 N)2
FC = 2868 N
αC aus dem Kräfteparallelogramm:
tan αC = FCx : FCy = 850 N : 2739 N = 0,31 –>
αC = 17°13´
4. Den Bremshebel freimachen.
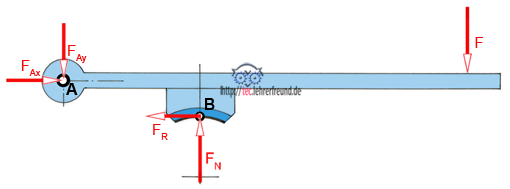
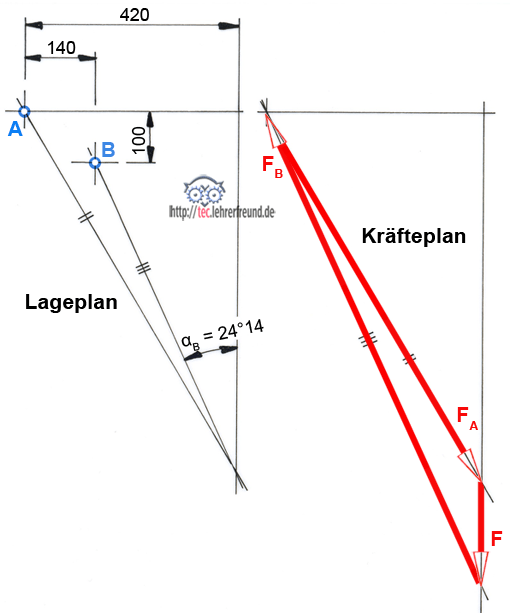
5. Die Kräfte F, FA und FB zeichnerisch ermitteln.
Die Größen und Richtungen von FA und FB sind nicht bekannt. Wir berechnen deshalb den Winkel αB. Dafür muss zuerst FB ermittelt werden.
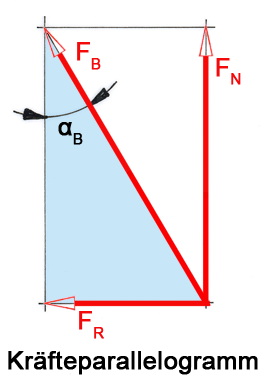
FB = √ FN2 + FR2 = √ (1889 N)2 + (850 N)2 =
FB = 2071 N
αB –> tan αB = FR : FN = 850 N : 1889 N = 0,45 –>
αB = 24°14´
Lageplan ML: 1 mm ≙ 10 mm
(d. h. 1 mm in der Zeichnung sind 10 mm in Wirklichkeit)
Kräfteplan MK: 1 mm ≙ 20 N