Kräfte: Unbekannte Kräfte zeichnerisch ermitteln (1) 02.10.2011, 09:21
Das Gleichgewicht von zwei Kräften finden, ist einfach. Etwas schwieriger wird es schon, wenn an einem Bauteil drei Kräfte angreifen. Am Beispiel eines Wanddrehkrans wird gezeigt, wie man in einem solchen Fall die Kräfte zeichnerisch ermittelt.
Beachten: Niveau Techn. Gymnasium, Berufskolleg u. Ä.
Zeichnerische Ermittlung unbekannter Kräfte
1. Zwei-Kräfte-Verfahren (Gleichgewicht von 2 Kräften)
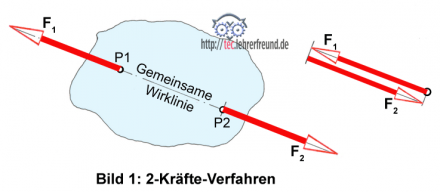
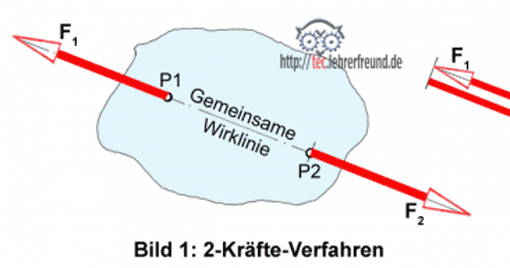
Zwei Kräfte F1 und F2 (Bild 1) sind nur dann im Gleichgewicht, wenn sie die gleiche Größe (F1 = F2 ) und Wirklinie, jedoch einen entgegengesetzten Richtungssinn haben.
Ist also die Kraft F1 die Resultierende einer Kräftegruppe, angreifend in P1, dann muss die Gleichgewichtskraft F2 = F1 sein und auf einer gemeinsamen Wirklinie angreifen, z. B. in P2. Das Krafteck muss sich schließen.
2. Drei-Kräfte-Verfahren (Gleichgewicht von drei nicht parallelen Kräften)
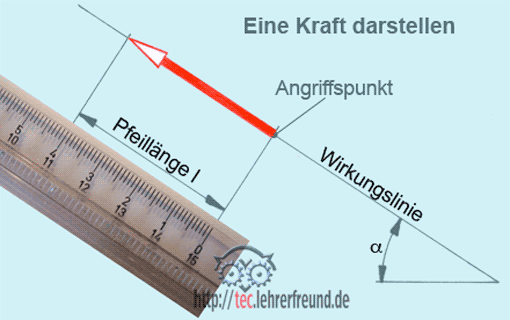
Anmerkung: Zur Lösung einer konkreten Aufgabe benötigt man einen Lageplan und einen Kräfteplan - beide in einem passenden Maßstab gezeichnet. Diese Maßstäbe sind für der Erläuterung der folgenden Verfahren zunächst nicht nötig.
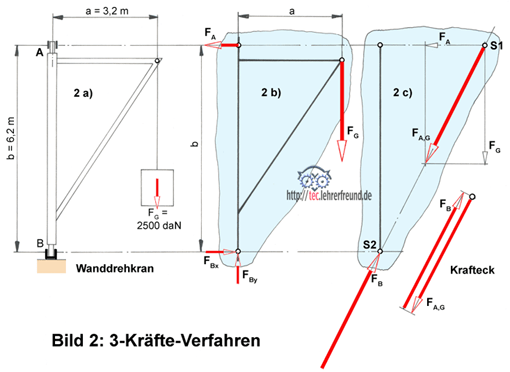
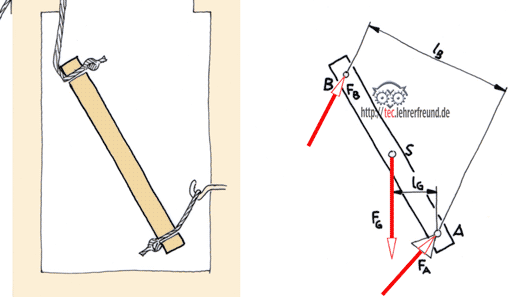
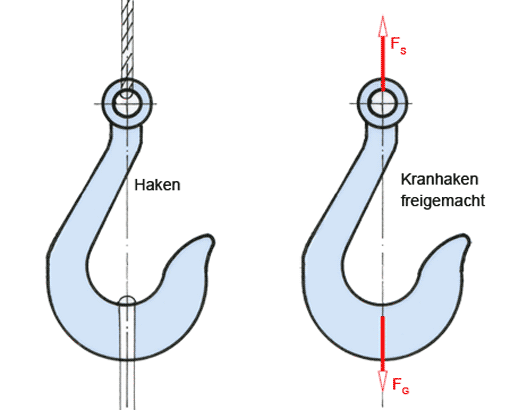
Aufgaben mit 3-Kräfte-Gleichgewicht sind häufig zu lösen. Der Wanddrehkran in Bild 2a) wird unten in einem zweiwertigen Stützlager B und oben in einem einwertigen Halslager A gehalten.
Ein einwertiges Lager (auch Loslager) überträgt nur senkrecht zur Stützebene liegende Kräfte. Sie werden oft dann verwendet, wenn das Lager eine Längsausdehnung zulassen soll.
Ein zweiwertiges Lager (auch Festlager) überträgt Kräfte in beliebiger Richtung. Die Lagerkraft kann in eine waagrechte x-Komponente und eine senkrechte y-Komponente zerlegt werden. Die Wirklinie der Lagerkraft wird erst durch die Gleichgewichtsbedingungen bestimmt. Gleichgewicht herrscht, wenn sich alle X-Kräfte, alle Y-Kräfte und alle am Körper angreifenden Drehmomente aufheben.
Aufgabe: Die Lagerkräfte in A und B sind zeichnerisch zu bestimmen.
Lösung: Am freigemachten Wanddrehkran - siehe Bild 2b) - der als starre, ebene Scheibe betrachtet werden kann, wirken die Kräfte:
- Last FG. Ihre Größe ist gegeben, Richtung und Wirklinie WL sind bekannt;
- Halslagerkraft FA, Größe unbekannt, Wirklinie bekannt (waagerecht), wegen des einwertigen Lagers;
- Stützlagerkraft FB, Größe unbekannt, Wirklinie unbekannt, wegen des zweiwertigen Lagers. Wir wissen nur, dass die Wirklinie durch das untere Lager gehen muss. Wir geben in diesem Fall die Wirklinien der horizontalen x- und der vertikalen y-Komponenten von FB an, also die Wirklinien der Kräfte FBx und FBy. Am Wanddrehkran wirken also drei Kräfte: FA, FB und FG. Die Konstruktion der noch unbekannten Wirklinie WL ist der wichtigste Teil bei der Lösung solcher Aufgaben.
Fassen wir gedanklich die Kräfte FA und FG, deren Wirklinien (Bild 2c) ja bekannt sind, zur Resultierenden FA,G zusammen, dann haben wir es wieder mit nur 2 Kräften zu tun (wie unter 1.). Angriffspunkt der Resultierenden FA,G ist der Punkt S1 (Bild 2c), der Schnittpunkt der Kräfte FA und FG. Zwischen FA,G und der Lagerkraft FB (2-Kräfte-Verfahren) kann nur Gleichgewicht herrschen, wenn sie auf derselben Wirklinie S1 - S2 liegen und ihr Krafteck geschlossen ist. Also muss die Wirklinie der Lagerkraft FB ebenfalls durch den Punkt S1 gehen.
Zusammenfassung:
Drei nicht parallele Kräfte sind im Gleichgewicht, wenn das Krafteck geschlossen ist und die Wirklinien der Kräfte sich in einem Punkt schneiden (Drei-Kräfte-Verfahren).
Lösung der Aufgabe kurz gefasst:
- Den Lageplan zeichnen (Bild 2c) und dort die Wirklinien der Kräfte FA und FG zum Schnitt S1 bringen. Damit ist ein zweiter Punkt der Wirklinie von FB gefunden.
Die Wirklinie muss durch das untere Stützlager und durch S1 gehen. Da jetzt alle Wirklinien bekannt sind, kann im Kräfteplan der geschlossene Kraftzug gezeichnet werden, womit auch die Größen der Kräfte FA und FB (auch FBx und FBy) bestimmt sind.
Die gefundenen Richtungen (Umfahrungssinn!) der Kräfte übertragen wir wie üblich in den Lageplan.
Arbeitsplan:
- Lageplan zeichnen mit freigemachtem Körper und damit Wirklinien der Belastungen und der einwertigen Lagerkraft festlegen;
- Bekannte Wirklinien zum Schnitt S1 bringen;
- Schnittpunkt S1 mit zweiwertigem Lagerpunkt S2 verbinden; damit ist die Wirklinie bekannt;
- Krafteck mit nach Größe und Richtung bekannter Kraft anfangen;
- Krafteck zeichnen (schließen!);
- Kraftrichtungen in den Lageplan übertragen.
_______________________
Das »Vier-Kräfte-Verfahren« behandeln wir in einem weiteren Beitrag.