Kräfte an einer Schubkarre - Culmannsche Gerade 15.10.2011, 09:01
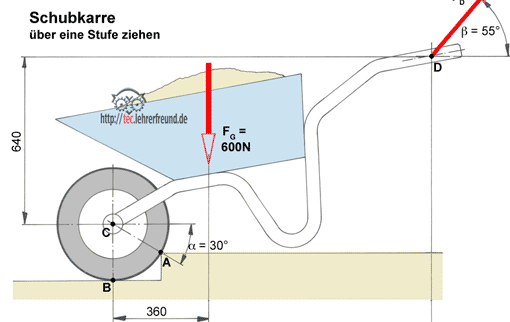
Wirken in einem System vier Kräfte, von denen drei unbekannt sind, dann hilft bei der Ermittlung dieser drei Kräfte die Culmannsche Gerade weiter. Das studieren wir am Beispiel einer Schubkarre.
Anwendung der Culmannschen Geraden
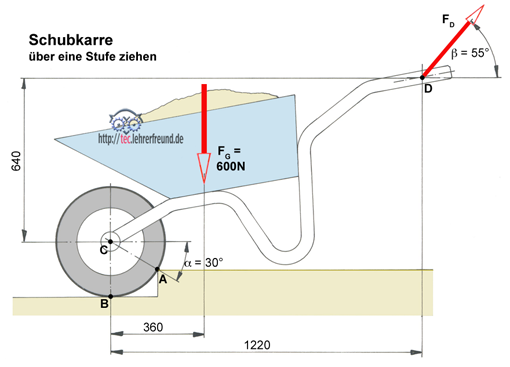
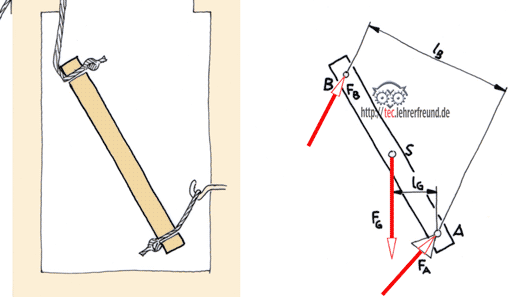
Eine Schubkarre soll rückwärts über eine Stufe gezogen werden.
Aufgabe
1. Rechnerisch:
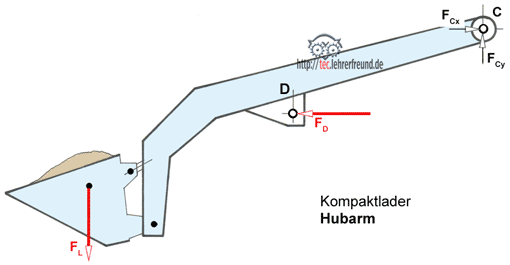
1 a. Die Gesamtzugkraft FD an den Schubkarrengriffen ist zu berechnen.
1 b. Die Kräfte FA und FB sind zu berechnen
2. Zeichnerisch:
Die Kräfte FA, FB und FD sind zu ermitteln.
Lösungsvorschläge
1 a.
I. Waagrechte Kräfte Σ Fx = 0 = FA · cos α - FD · cos β
II. Senkrechte Kräfte Σ Fy = 0 = FA · sin α – FG + FD · sin β + FB
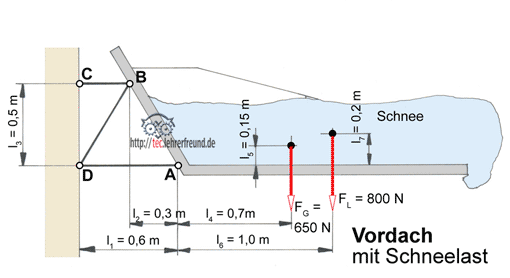
III. Momentengleichung um den Punkt C: Σ M(C) = 0 = FG · l2 + FD · cos β · l3 – FD · sin β · l1
(FA und FB erzeugen kein Drehmoment, weil die Hebelarme Null sind)
Aus Formel III. FD berechnen:
FD · sin β · l1 = FG · l2 + FD · cos β · l3
FD · sin β · l1 – FD · cos β · l3 = FG · l2
FD · (sin β · l1 – cos β · l3) = FG · l2
FD = FG · l2 : (sin β · l1 – cos β · l3)
FD = 600 N · 360 mm : (0,819 · 1220 mm – 0,574 · 640 mm) =
FD = 342 N
1 b.
Aus Formel I.: FA = FD · cos β : cos α = 342 N · 0,5736 : 0,866 =
FA = 227 N
Aus Formel II.: FB = FG – FA · sin α – FD · sin β =
FB = 206 N
2. Zeichnerisch:
Ermittlung der Kräfte FA, FB und FD.
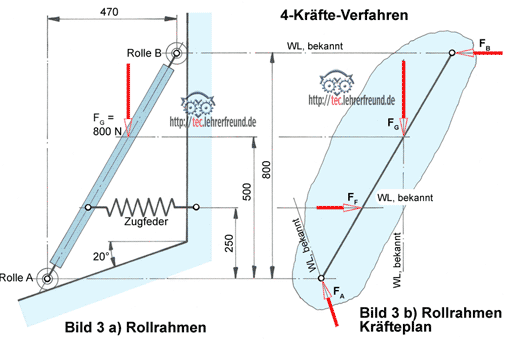
Wir wiederholen die einzelnen Schritte:
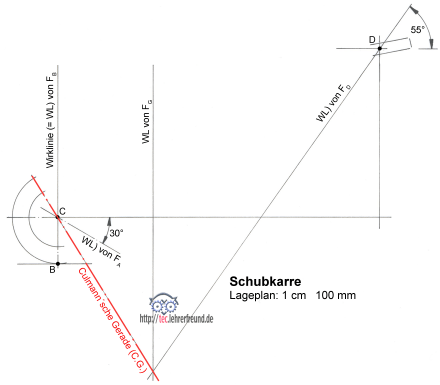
- Lageplan zeichnen mit freigemachtem Körper und damit die Wirklinien der Belastungen und Lagerkräfte festlegen;
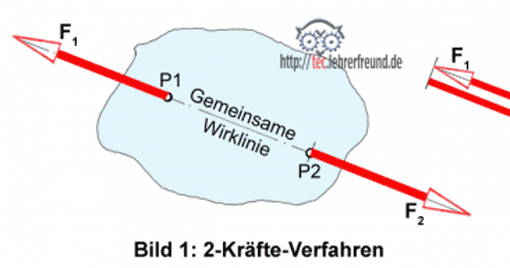
- Wirklinien je zweier Kräfte zum Schnitt bringen;
- Gefundene Schnittpunkte verbinden zur Wirkungslinie der beiden Resultierenden (= Culmannsche Gerade);
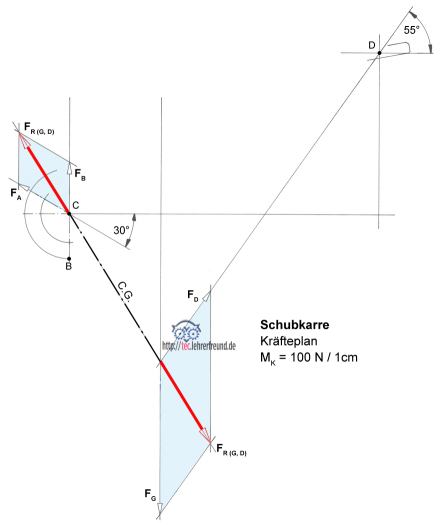
- Kräfteplan mit nach Größe und Richtung bekannter Kraft anfangen;
- Kräfteplan mit Culmannscher Geraden und den Wirklinien der anderen Kräfte schließen;
- Beachten: Die Kräfte eines Schnittpunkts im Lageplan ergeben ein Teildreieck im Kräfteplan.