Festigkeitsberechnungen (4): Biegung 17.12.2010, 10:12

Werden Bauteile auf Biegung beansprucht, dann entstehen im gebogenen Querschnitt Zug- und Druckspannungen. Bei der Berechnung der maximalen Biegespannung ist das »Widerstandsmoment« wichtig. Was versteht man darunter?

Beanspruchung von Bauteilen auf Biegung

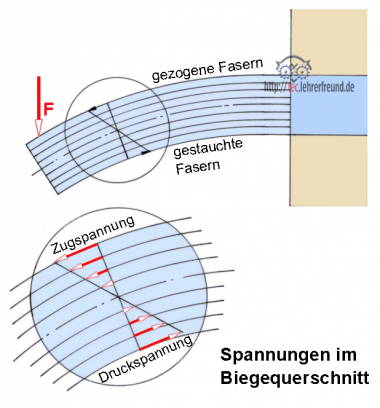
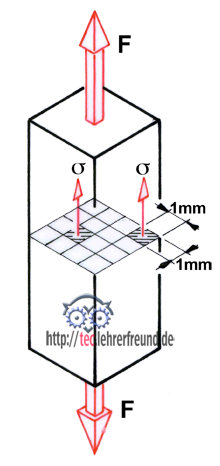
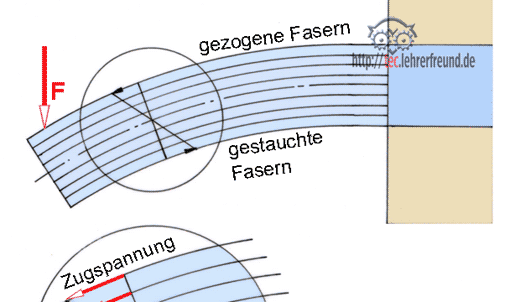
Bild: Die Kraft F beansprucht den Stab (auch Welle, Balken u. Ä.) auf Biegung. Die vor der Belastung gerade Stabachse wird gebogen. Unter einer Biegebelastung entstehen im Querschnitt Zug- und Druckspannungen.
Anmerkung: Um den Vorgang deutlich zu machen, sind die Durchbiegungen in den Skizzen stark übertrieben.

In den Randfasern entstehen die stärksten Spannungen, die neutrale Faserschicht (strichpunktiert) dagegen ist spannungslos. In symmetrischen Querschnitten sind die Zug- und Druckspannungen gleichmäßig (linear) über den Querschnitt verteilt.    
Die Biegespannung σ_b ist abhängig 
- vom Biegemoment M_b
- vom Widerstandsmoment W.

Berechnungsformel

Biegespannung σ_b = M_b : W (Ncm : cm³ = N/cm²)

Biegemoment M_b
Für einfache Belastungsfälle sind hier Formeln für die Berechnung des Biegemomentes M_b angegeben. Bei anderen Belastungsfällen findet man die Formeln in Tabellenbüchern.  

Häufig vorkommende Biegemomente M_b bei Belastung mit einer Einzelkraft sind
- der einseitig eingespannte Träger
- der auf zwei Stützen ruhende Träger 

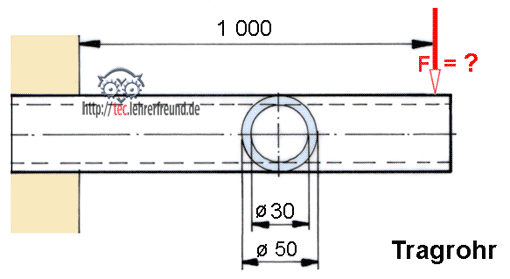
Beim einseitig eingespannten Träger ist M_b = F ∙ a

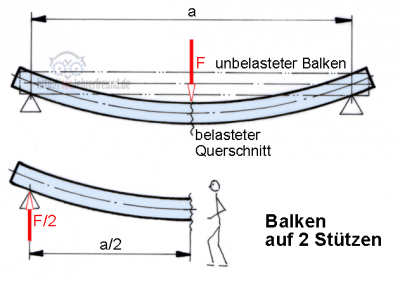
Bild unten: Auf zwei Stützen ruhender Träger. F wirkt in Balkenmitte.

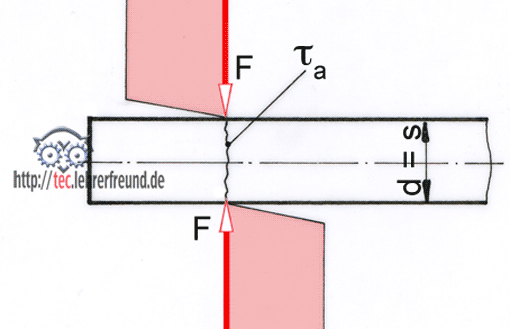
Wie erhält man beim auf zwei Stützen ruhenden Träger das Biegemoment? Man stellt sich in den Biegequerschnitt und schaut nach links (oder rechts): Die von dort erkennbare Kraft F/2 zusammen mit dem Abstand a/2 ergeben das Biegemoment: 

M_b = F/2 ∙ a/2 = F ∙ a : 4

Widerstandsmoment W
Zum Verständnis der Beanspruchungsart Biegung ist eine geometrische Betrachtung erforderlich. Bei der Zug-, Druck- und Abscherbeanspruchung spielt für Festigkeitsrechnungen neben der Kraft F nur die Querschnittsfläche S eine Rolle. Bei der Bestimmung der Zugspannung z. B. in einem Stab mit Kreisquerschnitt erscheint in σ_z = F : S (in N/mm²) die Flächenformel für den Kreisquerschnitt als geometrische Größe.   

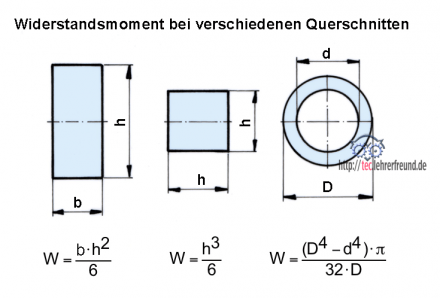
Für die Biegung (dies gilt auch für die Knickung und die Verdrehung) brauchen wir außer der Fläche S noch zwei andere geometrische Größen: das Trägheitsmoment I, Einheit cm⁴,  und das Widerstandsmoment W, Einheit cm³. Das Widerstandsmoment ist vom Trägheitsmoment abgeleitet. Für diese beiden Größen hat die höhere Mathematik Berechnungsformeln entwickelt.

Widerstandsmoment und Trägheitsmoment sind Größen, die dem Anfänger erfahrungsgemäß einige Schwierigkeiten bereiten, denn er kann sich nur wenig darunter vorstellen. Der Begriff Trägheitsmoment und die Einheit »cm⁴« werden ihn völlig verwirren. Er muss sich aber nicht mehr darunter vorstellen als dass er hier einfach eine von der Querschnittsform abhängige Rechengröße einsetzen muss. Ein einfacher Versuch gibt hierüber Aufschluss.

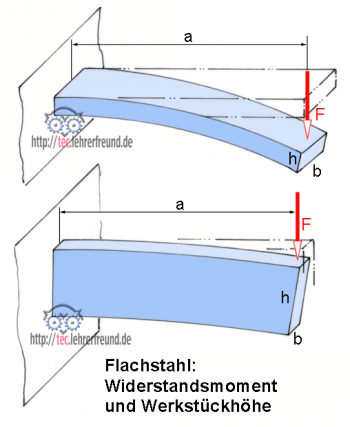
In der Skizze »Flachstahl: Widerstandsmoment und Werkstückhöhe« hat der Stab in beiden Fällen denselben Querschnitt b x h und wird jeweils von derselben Kraft F gebogen. Trotzdem wird er sich weniger verformen, wenn er wie in der Skizze unten, hochkant eingespannt ist. Diese Erkenntnis wird in der Berechnung mit dem Widerstandsmoment W berücksichtigt.

___________________________

Übungsaufgaben zur Biege-Berechnung nimmt sich der nächste Beitrag vor.

Weitere Informationen zum Thema Festigkeit finden Sie hier