Festigkeitsberechnungen (2) 21.10.2008, 08:48
Möchte man von einem Bauteil aus Stahl wissen, wie hoch es auf Zug belastet werden darf, dann muss man wenigstens zwei Informationen besitzen. Sie ergeben sich aus dem genormten Zugversuch.
3. und 4. Ausbildungsjahr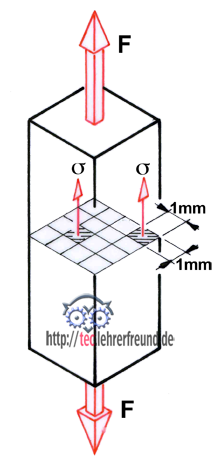
Wie Bauteile berechnet werden: Zugbeanspruchung
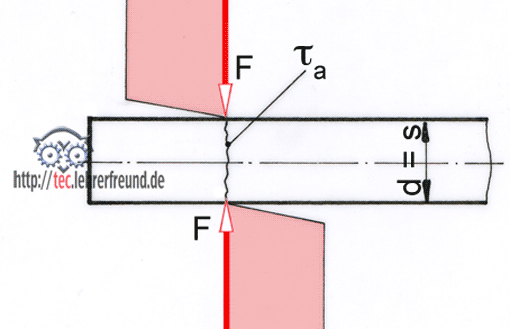
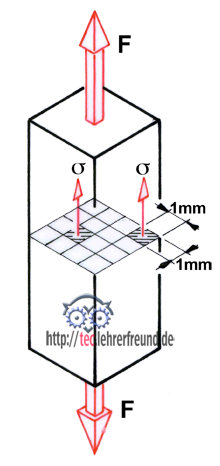
Skizze: Wird ein Stahlstab mit der Kraft F gedehnt, dann geht man davon aus, dass sich diese Kraft gleichmäßig auf die einzelnen Quadratmillimeter des Querschnitts S verteilt. Die pro Quadratmillimeter übertragene Kraft wird als Spannung σ (sigma, griech. Buchstabe) bezeichnet.
Daraus ergibt sich eine Berechnungsformel:
Zugspannung σz = F/S (in N/mm2)
Der Index z in σz bezieht sich auf »Zugbelastung«. Die folgenden Ausführungen gelten ähnlich für die Druckfestigkeit σd.
Möchte man von einem Bauteil aus Stahl wissen, wie hoch es auf Zug belastet werden darf, dann muss man wenigstens zwei Informationen im Voraus besitzen:
1. Wie verhält sich der Stahl, wenn er auf Zug beansprucht wird?
2. Welche Zugkraft (Spannung) hält der verwendete Stahl überhaupt aus?
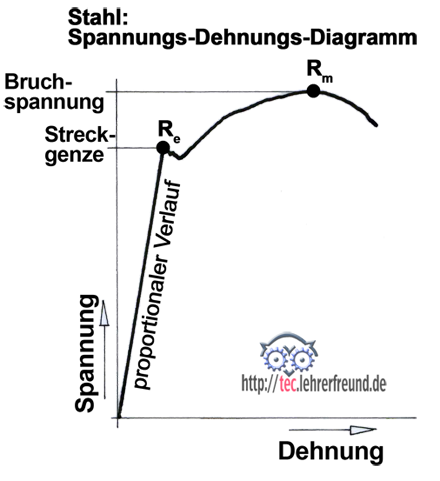
Zu 1. Diese Frage beantwortet ein genormter Zugversuch, dessen Ergebnisse wir hier verkürzt beschreiben (Skizze unten).
Stahl verhält sich beim Auseinanderziehen zunächst elastisch wie eine Zugfeder: Die Zugprobe verlängert sich im Verhältnis der Zugkraft, d. h.: doppelte Kraft, doppelte Verlängerung, dreifache Kraft, dreifache Verlängerung, usw. Dies ist ein proportionales Verhalten, das an einem bestimmten Punkt zu Ende ist. Dieser Punkt ist die Streckgrenze Re. Bei weiterer Belastung bricht die Zugprobe sehr schnell. Der höchste erreichte Spannungswert ist die Zugfestigkeit Rm. Die (alte) Stahlkurzbezeichnung St 37 (heute S235JR) besagt: Es handelt sich um einen Stahl, der ab einem Rm = 370 N/mm2 brechen darf.
Zu beachten: Die Spannungswerte mit dem Symbol R werden im Zugversuch ermittelt. Bei der Berechnung einer im praktischen Betrieb auftretenden Spannung wird diese mit dem Symbol σ (sigma) bezeichnet.
Im proportionalen Bereich geht ein eingebautes Teil nach Entlastung wieder auf seine Ursprungslänge zurück. Bei einer weiteren Belastung, also rechts von Re, ist dies nicht mehr der Fall: Eine solche Belastung würde im Bauteil eine bleibende Verlängerung hervorrufen. Dies darf in einem eingebauten Maschinenteil in keinem Fall geschehen: Es muss unter der Betriebsbelastung immer unterhalb Re bleiben. Eine Möglichkeit, sich im ungefährdeten Bereich zu bewegen, ist, mit einer Sicherheitszahl zu arbeiten. Die Sicherheitszahl ν (griech. nü) = 3 besagt dann: Ein Stahl St 37 darf höchstens mit 370 N/mm2 : 3 = ca. 123 N/mm2 belastet werden. Dazu eine Rechnung:
Eine Schraube aus Stahl mit Rm = 600 N/mm2 hat einen belastbaren Kernquerschnitt von 7,8 N/mm2. Es wird eine Sicherheit gegen Bruch von 2,5 verlangt.
a) Welche zulässige Spannung σzul darf im Schraubenstahl höchstens auftreten?
b) Mit welcher Zugkraft darf die Schraube höchstens belastet werden?
a) σzul = Rm : ν = 600 N/mm2 : 2,5 = 240 N/mm2
b) Fzul = S • σzul = 7,8 mm2 • 240 N/mm2 = 1872 N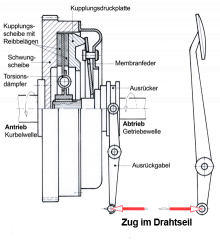
Aufgaben:
1. Einscheibenkupplung: Im Zugseil wirkt eine Zugkraft F = 420 N. Der Seilwerkstoff soll mit höchstens 90 N/mm2 beansprucht werden. Welcher Drahtquerschnitt ist erforderlich?
Lösung: S = 4,67 mm2
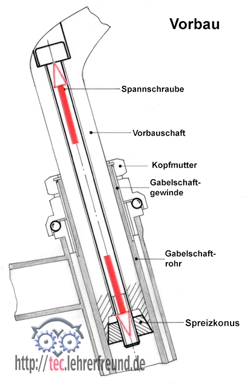
2. Fahrradvorbau: Die Spannschraube mit 8 mm Schaftdurchmesser soll mit maximal 500 daN angezogen werden. Wie groß ist σ im Schaftquerschnitt?
Lösung: σ = 99,47 N/mm2
Auch hier erfahren Sie etwas zum Thema Festigkeitslehre.
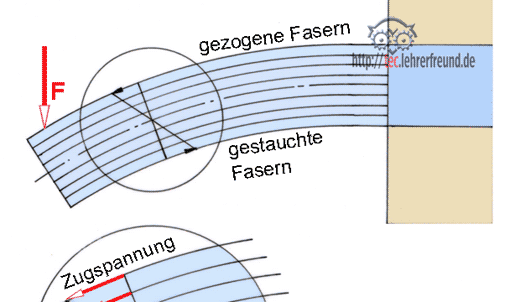
Ebenso hier: Biegung