Festigkeitslehre Überblick (2) 04.02.2015, 06:57
Kräfte und Drehmomente, die auf Maschinenteile wirken, beanspruchen diese auf unterschiedliche Weise. Die Bauteile müssen so dimensioniert sein, dass sie der Belastung standhalten. Im zweiten Teil geht es um Beanspruchungsarten und Spannungswerte.
Festigkeitslehre
Die Festigkeitslehre ist ein Bereich innerhalb der Technischen Mathematik. In Berufsschulen ermittelt man mit Festigkeitsberechnungen, welchen Belastungen ein Bauteil standhält. Dabei erfährt man etwas
– über die Sicherheit und Langlebigkeit von belasteten Bauteilen,
– oft auch über die Herstellung und Wartung belasteter Bauteile.
Lasten, Eigengewicht, Gasdrücke, Zahnkräfte, Zerspanungswiderstände, Reibungswiderstände usw. erzeugen an technischen Bauteilen Belastungskräfte. Mit den Verfahren der Statik werden die Kräfte ermittelt, die den Körper im Gleichgewicht halten. Die Ermittlung dieser Kräfte ist meist der erste Schritt zur Konstruktion eines Bauteils; sie sind auch die Grundlage der Festigkeitsrechnung.
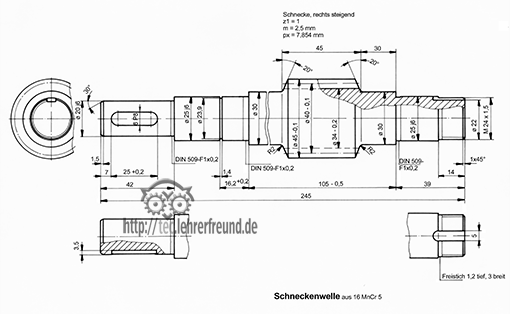
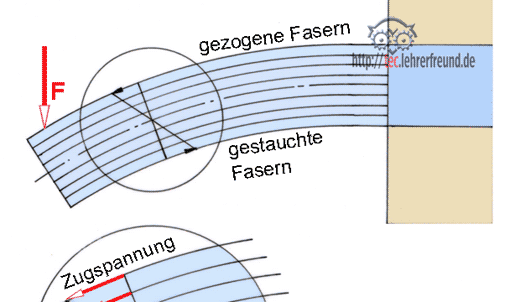
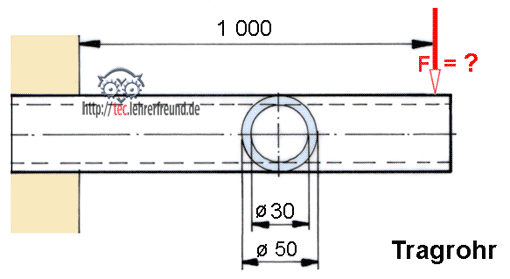
Bild unten: Wir beziehen uns auf den Beitrag »Festigkeitslehre Überblick (1)«. Für die Dimensionierung und Herstellung der Getriebewelle müssen die an der Welle angreifenden Kräfte bekannt sein. Die wichtigsten Größen der Statik sind die Kraft F (Kurzzeichen F von engl. force), die in Newton (N), Dekanewton (daN), Kilonewton (kN) oder Meganewton (MN) gemessen und angegeben wird, und das Drehmoment M der Kraft F, mit seinen Einheiten Newtonmeter (Nm), Newtonzentimeter (Ncm) oder Newtonmillimeter (Nmm). Momente werden nach ihrer Auswirkung benannt; so wird in der Festigkeitslehre ein biegendes Kraftmoment als Biegemoment Mb und ein das Bauteil tordierendes (verdrehendes) Kraftmoment als Torsionsmoment MT bezeichnet.
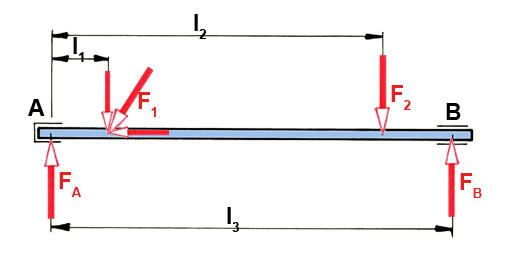
Die Auswahl geeigneter Werkstoffe sowie die richtige Dimensionierung helfen in der Praxis, die Herstellungs- und Wartungskosten zu senken.
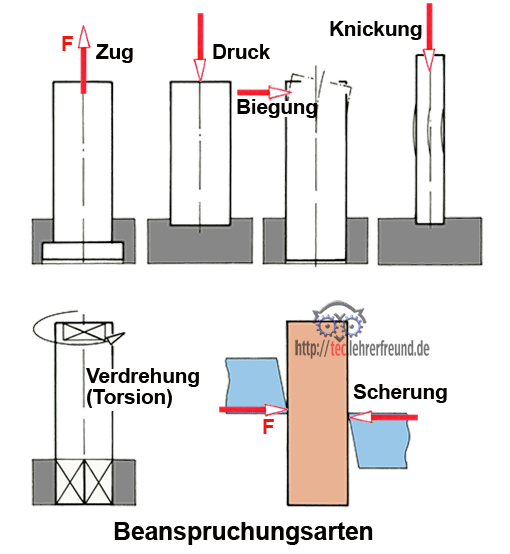
Beanspruchungsarten bei Belastungen
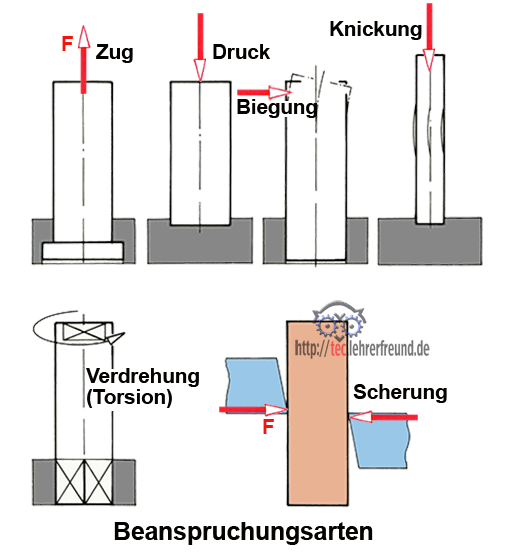
Bauteile werden bei Belastung unterschiedlich beansprucht. Beanspruchungsarten sind:
Beanspruchung auf Zug
Beanspruchung auf Druck
Beanspruchung auf Knickung
Beanspruchung auf Biegung
Beanspruchung auf Scherung
Beanspruchung auf Verdrehung
Die Getriebewelle oben wird auf Druck und Biegung beansprucht.
Spannung im Werkstoff bei Belastungen
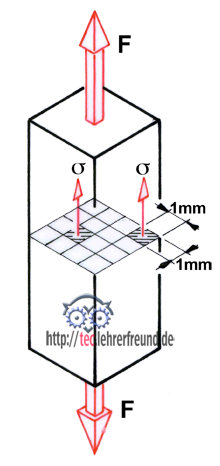
Wird ein Bauteil belastet, entstehen im Werkstoff innere Kräfte, die man mit dem Begriff »Spannung« bezeichnet. Mit elektrischer Spannung hat die Spannung in der Festigkeitslehre nichts zu tun. Rechnerisch ist eine Spannung immer eine auf 1 mm2 Querschnitt bezogene Kraft. Wichtige Spannungsarten sind:
Zugspannung (bei Beanspruchung auf Zug), Formelzeichen σz (sigma)
Druckspannung (bei Beanspruchung auf Druck), Formelzeichen σd
Knickspannung (bei Beanspruchung auf Knickung), Formelzeichen σk
Biegespannung (bei Beanspruchun auf Biegung), Formelzeichen σb
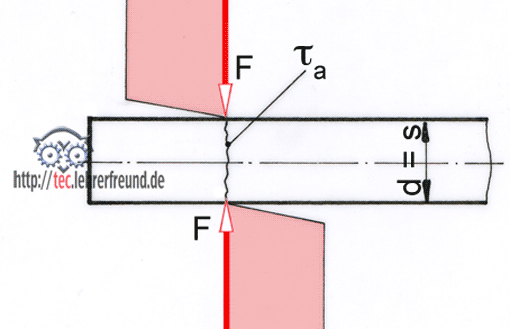
Scherspannung (bei Beanspruchung auf Scherung), Formelzeichen τa (tau)
Torsionsspannung (bei Beanspruchung auf Verdrehung, Torsion), Formelzeichen τt
Solche Spannungen sind in der Lage, den Werkstoff zu verformen. Je nach Verformungsgrad spricht man von elastischer oder plastischer Verformung.
Elastisch hat sich ein Bauteil unter Belastung verformt, wenn es nach Entlastung wieder in seinen Ursprungszustand zurückkehrt. Wenn man z. B. einen Metallstab zieht, dehnt er sich wie ein Gummiseil. Wird die Last weggenommen, geht der Metallstab – wie auch das Gummiteil – wieder in seine Ursprungsform zurück.
Ist jedoch die belastende Kraft sehr groß, kann sich das Bauteil bleibend oder »plastisch« verformen. Bei eingebauten Bauteilen darf es so weit nicht kommen, denn dieser Fall würde zu ihrer Zerstörung führen.
Die Grenzen der elastischen Verformung eines Bauteils werden wie folgt bezeichnet:
Streckgrenze (bei Zugspannung), Formelzeichen Re
Quetschgrenze (bei Druckspannung), Formelzeichen σdF
Biegegrenze (bei Biegespannung), Formelzeichen σbF
Verdrehgrenze (bei Verdrehung, Torsion), Formelzeichen τtF
Bei Abscherung und Knickung verhalten sich Metalle nicht elastisch. Bleibende Formänderungen (plastische Verformungen) werden wie folgt benannt:
Dehnung (bei Zugspannung), Formelzeichen ε
Stauchung (bei Druckspannung), Formelzeichen εd
Biegung (bei Biegespannung), Formelzeichen f = Differenz zwischen der ursprünglichen Position des Bauteils und der, nachdem es mit der Biegekraft gebogen wurde.
Verdrehwinkel (bei Verdrehung, Torsion), Formelzeichen φ (phi)