Reibung (3): Übungsaufgaben 22.03.2011, 09:14

Aus den zahllosen technischen Beispielen, in denen Reibung vorkommt, greifen wir heraus: Seilbahn, Schraubverbindung, Fahrrad, einen Material-Förderkübel. Diese Beispiele werden durchgerechnet.

Dem Thema voraus geht »Reibung (2): Haftreibung, Gleitreibung, Rollreibung«

Reibung: Übungsaufgaben

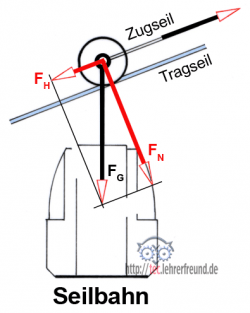
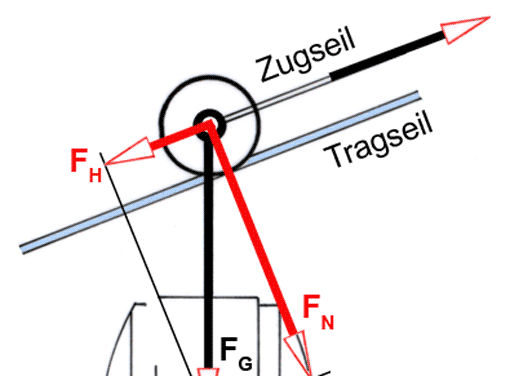
1. Seilbahn

Das Tragseil verläuft unter 35° zur Horizontalen. Gesamtgewicht Kabine + Aufhängung + Beladung F_G = 3800 N. Zu berechnen:

a) F_H und F_N

b) Die Rollreibkraft, wenn f = 4 mm ist.

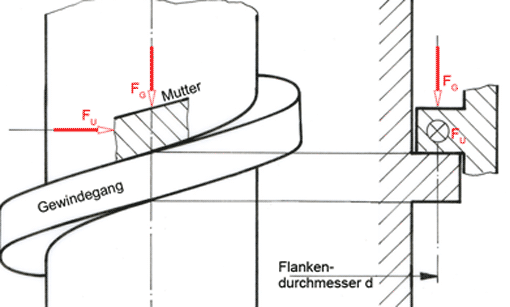
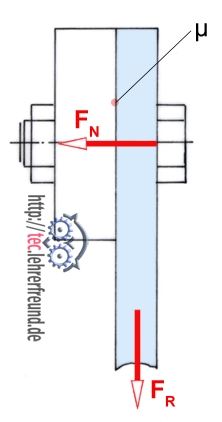
2. Schraubverbindung 

Auf den Stab wirkt eine Zugkraft von 1,8 kN. Die Reibungszahl μ = 0,19.

Mit welcher Mindestkraft muss F_N muss die Schraube auf den Stab drücken, wenn er nur durch Reibung in seiner Lage gehalten werden soll?

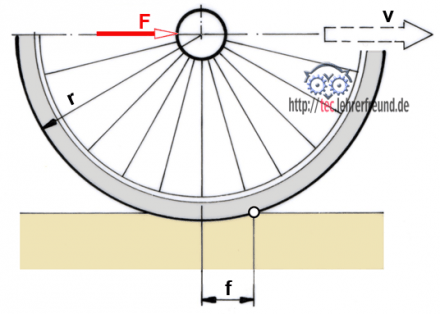
3. Fahrrad: Fahrwiderstand 

Reifendurchmesser 24"

Reifendruckkraft F_N = 420 N

f = 40 mm

Welche Rollkraft F muss aufgebracht werden?

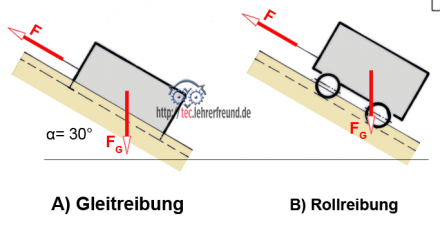
4. Kräfte am Förderkübel 

Ein F_G = 1 Tonne schwerer Transportkübel wird unter 30° nach oben gezogen

A) auf einer Gleitbahn

B) auf Rädern. 

Aufgaben für die Situation A): 

a) Das Kräfteparallelogramm ist zu skizzieren

b) Berechnen: Mit welcher Kraft drückt der Kübel auf die Fahrbahn?

c) Berechnen: Wie groß ist F ohne Berücksichtigung der Reibung?

d) Welche Kraft ist zum Hochziehen erforderlich, wenn μ = 0,3 ist?

Aufgabe für die Situation B):

e) μ_R = 0,01. Wie groß ist F?

Lösungen:

1. Seilbahn

(Vergleiche auch Winkelfunktionen)

α = 35°
F_G = 3 800 N

a) F_N :  cos α  = Ankathete : Hypotenuse = F_N : F_G

F_N = F_G ∙ cos 35° = 3 800 N ∙ 0,819 = 3 113 N

F_H :  sin α  = Gegenkathete : Hypotenuse = F_H : F_G

F_H = F_G ∙ sin 35° = 3 800 N ∙ 0,574 = 2 180 N

2. Schraubverbindung

F_R = μ  ∙  F_N

F_N = F_R : μ = 1800 N : 0,19 =

F_N = 9 474 N

3. Fahrrad: Fahrwiderstand 

Raddurchmesser d = 24" = 24" ∙ 2,54 cm/Zoll =  60,96 cm
r = 30,48 cm

F =  F_N • f / r = 420 N • 4 cm : 30,48 cm =

F = 55, 1 N

4. Kräfte am Förderkübel 

a) Kräfteparallelogramm:

b)

F_G = 1 Tonne ≈ 1 000 daN

F_N :  cos α  = Ankathete : Hypotenuse = F_N : F_G

F_N = F_G ∙ cos 30° = 1 000 daN ∙ 0,866 = 

F_N = 866 daN

c)

F = F_H : sin α  = Gegenkathete : Hypotenuse = F_H : F_G

F = F_H = F_G ∙ sin 30° = 1 000 daN ∙ 0,5 =

F = 500 daN        

d)

Die Reibkraft F_R und die Hangabtriebskraft F_H summieren sich: 

F_R = μ  ∙  F_N = 0,3 ∙ 866 daN = 259,8 daN

F = F_R +  F_H = 500 daN + 259,8 daN =

F = 759,8 daN

e)

Kübel auf Rollen:

F = F_R +  F_H = 500 daN + 0,01 ∙ 500 daN = 

F = 505 daN