Reibung in Gewinden 16.08.2012, 08:11
Im tec.LEHRERFREUND-Beitrag »Einfache Maschinen« ist ein Abschnitt dem Gewinde gewidmet. In den Überlegungen dazu wurde die Reibung vernachlässigt. Weil sie bei Gewinden aber eine entscheidende Rolle spielt, wollen wir sie in diesem Beitrag besprechen.
Lernniveau: Technische Oberschule, Berufskolleg u. Ä.
Reibung in Gewinden
Im tec.LEHRERFREUND-Beitrag »Einfache Maschinen« befasst sich ein Abschnitt mit dem Gewinde. In den Überlegungen dazu wurde die Reibung vernachlässigt. Weil sie bei Gewinden aber eine entscheidende Rolle spielt, wollen wir sie in diesem Beitrag besprechen.
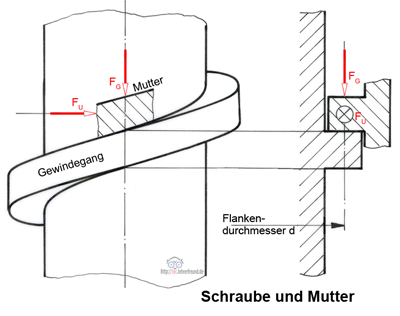
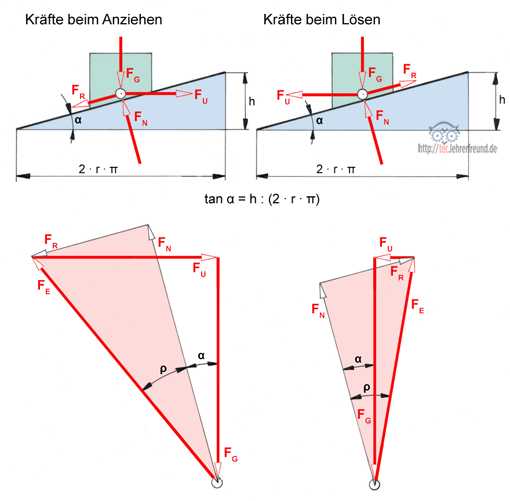
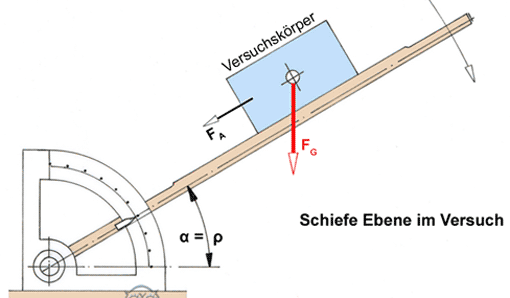
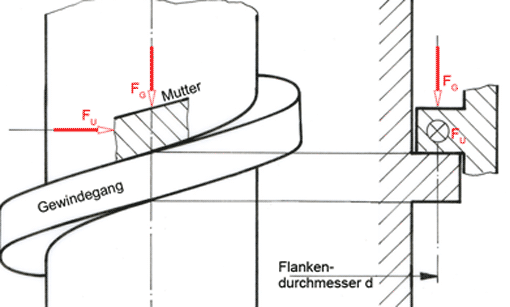
Das Anziehen oder Lösen einer Schraubenverbindung (zunächst mit Flachgewinde Bild oben) ist nichts anderes als das Hinaufschieben oder Herabziehen einer Last auf einer schiefen Ebene. Schiebende Kraft ist die waagrechte Umfangskraft FU. Vereinfachend lässt man dabei alle Kräfte an einem Punkt des Gewindegangs angreifen, der auf dem Flankendurchmesser d (Radius r) liegt. Dies ist zulässig, weil die Reibung von der Flächengröße unabhängig ist.
Im folgenden Text und in den Bildern sind
FG = Schraubenlängskraft (in Schraubenverbindungen auch die »Vorspannkraft«);
FU = die am Flankenradius r angreifend Umfangskraft;
FR = Reibkraft im Gewinde;
FN = Normalkraft zwischen den Gewindegängen,
α = Steigungswinkel des Gewindegangs;
tan α = h : (2 • r • π);
h = Steigung der Schraubenlinie;
ρ (= rho) = Reibwinkel;
tan ρ = μ = Gewindereibwert (siehe Reibung auf der Schiefen Ebene).
Die Bilder unten zeigen die Kraftecke für das Anziehen und Lösen der Schraubenverbindung. Beim Lösen der Schraubenverbindung haben Umfangskraft FU und Reibkraft FR umgekehrte Richtungen. Der Reibwinkel ρ ist hier größer als der Steigungswinkel α angenommen (ρ > α), so dass Selbsthemmung vorliegt.
Arbeitsschritte:
- Zum Konstruieren der Kraftecke zuerst die Normalkraft FN zeichnen,
- senkrecht an FN die Reibkraft FR zeichnen,
- beide Kräfte zur Ersatzkraft FE zusammenfassen,
- FE in eine senkrechte und eine waagerechte Kraft (FG und FU) zerlegen.
Aus den Kraftecken kann man die Berechnungsformeln ableiten:
- Umfangskraft zum Anziehen der Schraubenverbindung FU = FG • tan (α + ρ)
- Umfangskraft zum Lösen der Schraubenverbindung FU = FG • tan (α – ρ)
Bei ρ < α (der Reibwinkel ist kleiner als Steigungswinkel) ist keine Selbsthemmung vorhanden.
Formel für das Lösen der Schraubenverbindung: FU wird negativ, d.h. die Verbindung löst sich von selbst.
Beim Berechnen gibt es oft eine Schwierigkeit: Ist (ρ — α) oder (α — ρ) richtig? Keine der beiden Entscheidungen wäre ein Weltuntergang, denn es zählt das Ergebnis: Ist der Steigungswinkel α größer als der Reibwinkel ρ, heißt dies: Die Verbindung ist nicht selbsthemmend; sie löst sich mit FU selbst. Ist der Steigungswinkel α kleiner als der Reibwinkel ρ: Selbsthemmung; die Verbindung muss mit FU gelöst werden.
Befestigungsschrauben sind wegen ihres kleinen Steigungswinkels selbsthemmend. Bewegungsschrauben (z. B. Trapezgewinde) können bei mehrgängiger Ausführung selbstlösend sein.
Wir schreiben schließlich die Formeln in der üblichen Form:
Umfangskraft FU = FG • tan (α ± ρ) (+) für das Anziehen, (-) für das Lösen
Die Umfangskraft FU erzeugt am Radius r ein Gewindereibmoment MG:
MG = FU • r
MG = FU • r • tan (α +/- ρ) (+) gilt für das Anziehen, (-) für das Lösen.
____________
Aufgabe dazu:
Eine Schraube mit Gewinde M 24, Steigung 3 mm, Flankendurchmesser 22,051 mm wird mit FU = 300 N angezogen. μ = 0,3. Welche Anpresskraft entsteht?
Umfangskraft FU = FG • tan (α + ρ) ––> FG = FU : tan (α + ρ) =
tan α = h : 2 • r • π = 3 mm : (2 • 22,051/2 • π) = 0,043 ––> α = 2° 28´
tan ρ = μ = Reibwert im Gewinde ––> μ = tan ρ = 0,3
FG = 300 N : tan (0,043 + 0,3) = 300 N : 0,343
FG = 874,6 N