Reibung auf der Schiefen Ebene 03.08.2012, 06:45
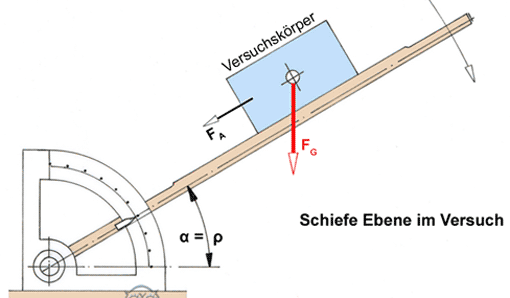
Mit der Versuchseinrichtung »Verstellbare Schiefe Ebene« kann man Reibzahlen bestimmen. Den daraus resultierenden Kräfteplan prüfen wir mit Hilfe der rechnerischen Gleichgewichtsbedingungen nach.
Lernniveau: Technische Oberschule, Berufskolleg u. Ä.
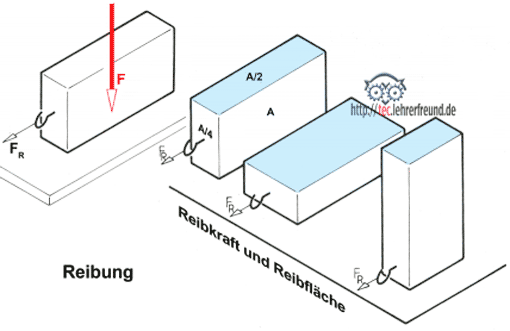
Wie man die Reibzahl μ bestimmt
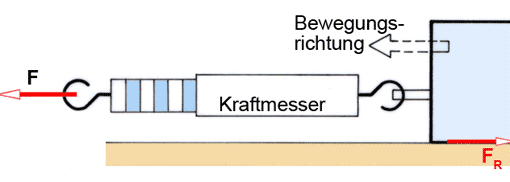
Die Reibzahlen kann man mit der Versuchseinrichtung »Verstellbare Schiefe Ebene« bestimmen. Der Versuchskörper bleibt bis zum Haftreibwinkel ρH in Ruhe und fängt an zu rutschen, wenn die Abtriebskraft FA = FG • sin ρ die Haftreibung zu überwinden beginnt; in diesem Fall ist FA = FR.
Die Neigung der schiefen Ebene entspricht dann dem Reibwinkel ρ = α.
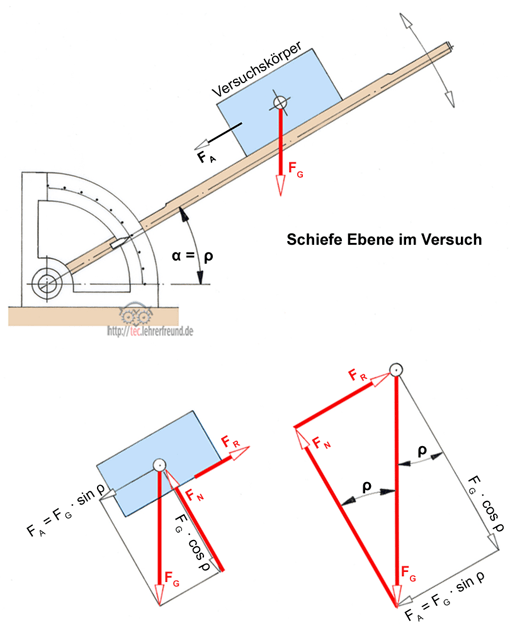
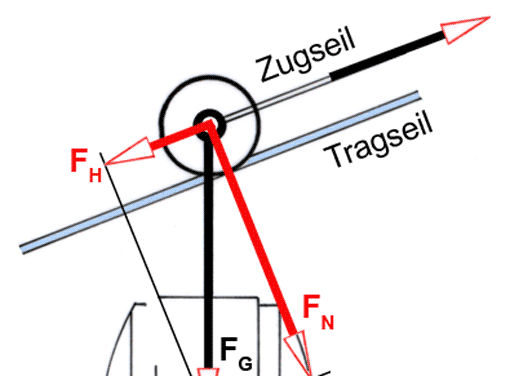
Zeichnung:
Oben die Versuchsanordnung mit einem einstellbaren Hebel. Der Hebelwinkel ist α.
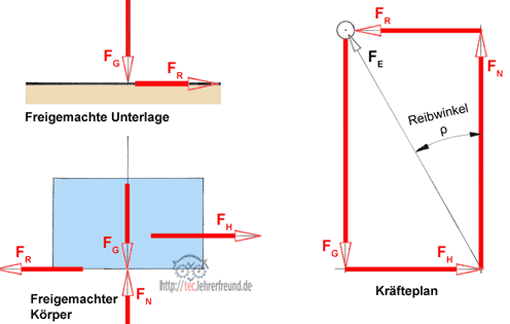
Skizzen darunter: Links ist der Versuchskörper freigemacht. Rechts der Kräfteplan.
Der Kräfteplan zeigt: tan ρ = FR : FN = μ –> tan ρ = μ
Mit den rechnerischen Gleichgewichtsbedingungen muss man zum gleichen Ergebnis kommen. Die x-Richtung liegt dabei auf der Schiefen Ebene, die y-Richtung senkrecht dazu.
I. ΣX = 0 = – FG • sin ρ + FN • μ
II. ΣY = 0 = + FN – FG • cos ρ; daraus ergibt sich:
FG • sin ρ = FN • μ
FG • cos ρ = FN
Teilt man die beiden Gleichungen durcheinander, dann ergibt sich:
FG • sin ρ : FG • cos ρ = μ = tan ρ, also tan ρ = μ (Trigonometrie: sin ρ : cos ρ = tan ρ)
Verändert man den Neigungswinkel α, dann verharrt der Körper in Ruhe, so lange α = ρH bleibt, d. h. so lange
tan α = tan ρH bzw.
tan α = μH ist. Dies ist die Selbsthemmungsbedingung.
Aufgaben
1. Die Kunststoffschuhe eines Supports bewegen sich auf einer Stahlbahn. Der Reibwinkel der Paarung wird mit 7° angegeben. Welcher Reibzahl μ entspricht er?
2. Auf einer schiefen Ebene mit einem Steigungswinkel von 12° wird eine 15 000 N schwere Last aufwärts bewegt. Die Reibzahl μ ist 0,1.
a) Welche Kraft ist erforderlich, um den Körper hoch zu ziehen?
b) Mit welcher Kraft wird der Körper nach unten gedrückt?
c) Ist die schiefe Ebene selbsthemmend?
Lösungsvorschläge
1. μ = tan ρ = tan 7° = 0,123
2. a) Beim Hochziehen müssen sowohl die Hangabtriebskraft FA als auch die Reibkraft FR überwunden werden.
Fhochziehen = FA + FR
= FG • sin ρ + FN • μ
= FG • sin ρ + FG • cos ρ • μ
= 15 000 N • 0,208 + 15 000 N • 0,978 • 0,1 =
= 3 120 N + 1 480,5 N
Fhochz = 4600,5 N
b) Wenn der Körper die schiefe Ebene hinab gleitet, bremst die Reibungskraft FR und wirkt gegen FA:
Fab = FA – FR
Fab = 3120 N – 1 480,5 N
Fab = 1 639,5 N
c) Selbsthemmung stellt sich ein bei tan α < μ
tan α = 0,2126 ist größer als μ = 0,1, also keine Selbsthemmung.