Einfache Maschinen (1) 27.06.2012, 07:39
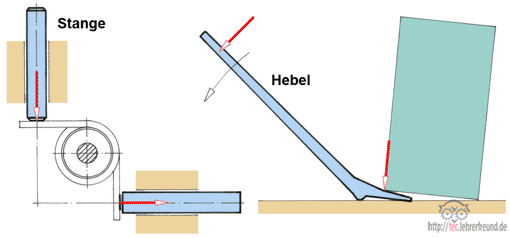
Es gibt vier grundlegende, einfache Maschinen: Seil und Stange, Rolle, Hebel, Schiefe Ebene. Jede aufwendigere Maschine ist eine Kombination von einfachen Maschinen. Die Berechnung einfacher Maschinen erlaubt einen Einblick in die Welt der Technischen Mechanik.
Einfache Maschinen
Unter einer einfachen Maschine versteht man in der Technischen Mechanik eine Einrichtung, mit der sich auf einfache Weise Kraft einsparen lässt. Dabei werden Angriffspunkt, Richtung oder Größe der Kraft verändert; wenn der Weg, der dabei zurückgelegt wird, größer wird, liegt das Gesetz vor, das man die »Goldene Regel der Mechanik« nennt. Sie besagt: Für das, was man an Kraft spart, muss man im gleichen Verhältnis mehr Weg aufwenden.
Jede mechanische Maschine ist eine Kombination von einfachen Maschinen.
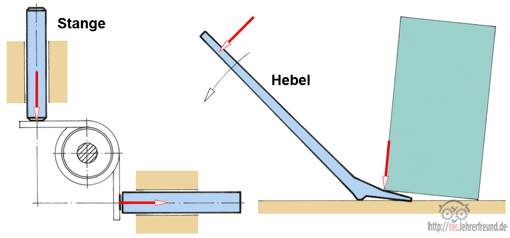
Es gibt vier grundlegende, einfache Maschinen, die sich nicht weiter vereinfachen lassen:
- Das Seil und die Stange: Sie verlagern den Angriffspunkt einer Kraft.
- Der Hebel: Er verändert den Angriffspunkt und Größe einer Kraft, und kehrt ihre Richtung um.
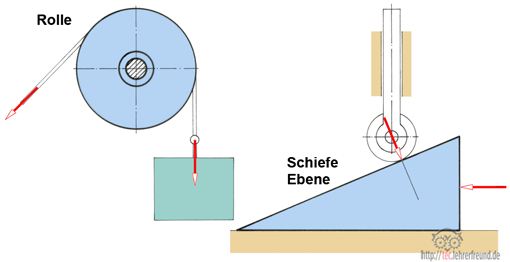
- Die Rolle: Sie verlagert den Angriffspunkt und Richtung der Kraft und lenkt sie um.
- Die Schiefe Ebene: Sie verändert die Größe und Richtung einer Kraft.
Das Gewinde ist eine um einen Zylinder gelegte mehrfache Schiefe Ebene.
1. Schiefe Ebene und Keil
Beachten: Bei Aufgaben zur schiefen Ebene oder zum Keil ist die mechanische Arbeit eine wichtige Ausgangsgröße: Arbeit W = F • s (in Nm). Beim Bewegen wird der Maschine eine Arbeit zugeführt, die am Ausgang des Systems wieder abgegeben wird. Es gilt: Die zugeführte Arbeit W1 und die abgegebene Arbeit W2 sind gleich groß, oder:
W1 = W2 (in Nm)
F1 • s1 = F2 • s2
Diese Berechnungsformel lässt die in der Maschine auftretende Reibung außer Acht. Sie kann aber bei Keilen und Gewinden erheblich sei.
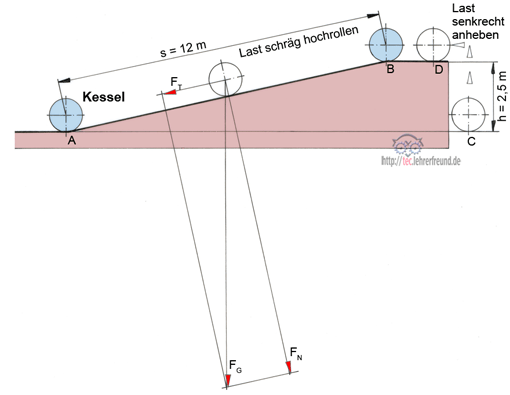
Bild: Ein 2800 N schwerer Kessel wird von A nach B gerollt, dann mit dem Kran von C nach D gehievt.
a) Welche Arbeit wird beim Heben des Kessels aufgewendet?
b) Wie groß ist die zum Rollen erforderliche Kraft?
Lösung:
a) Last heben: W = FG • h = 2 800 N • 2,5 m = 7 000 Nm
b) Last rollen: W = FT • s =
FT wird zeichnerisch ermittelt: FT = 580 N –> W = 6 960 Nm ≈ 7 000 Nm (Zeichenungenauigkeit)
Fazit: In beiden Fällen ist die gleiche Arbeit erforderlich.
FT rechnerisch:
FT = W : s = 7 000 Nm : 12 m = 583,3 N
Keil
Keile finden in der Technik ein breites Einsatzgebiet. Sie bilden die Grundform von Zerspanungswerkzeugen; mit ihnen werden Bauteile befestigt, Maschinen ausgerichtet usw.
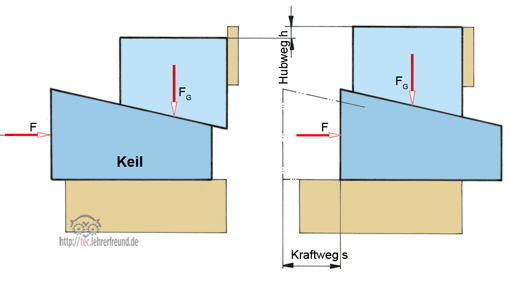
Bild: Mit einem Keil wird eine schwere Last FG = 2500 N feinfühlig nach oben bewegt. Wenn der Keil dabei unter der Keilkraft F um s = 200 mm nach rechts verschoben wird, hebt er die Last um h = 18 mm an. Die Keilkraft F ist zu berechnen.
Lösung:
W1 = W2
F • s = FG • h
F = FG • h : s = 2 500 N • 18 mm : 200 mm =
F = 225 N
Schraube und Mutter
Geometrisch ist ein Gewindegang eine um einen Zylinder gelegte Schiefe Ebene.
Bild: Schraube. Das Anziehen oder Lösen einer Schraubenverbindung (im Bild mit Flachgewinde) entspricht dem Hinaufschieben oder Herabziehen einer Last auf einer schiefen Ebene; schiebende Kraft ist die waagerechte Umfangskraft FU. Wir beziehen alle Kräfte auf einen Punkt an einem Gewindegang im Zylinderschnitt mit dem Flankendurchmesser d. In praktischen Berechnungen wird man vereinfacht den Außendurchmesser einsetzen.
Anmerkung: Wegen der hohen Flankenreibung haben Schrauben einen schlechten Wirkungsgrad von etwa 30%.
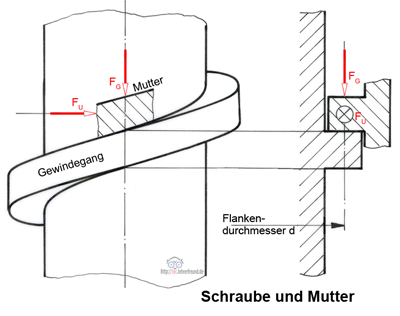
Schraube: Dreht man den Schraubenkopf mit der Kraft FU ein Mal, dann legt er den Umfangsweg s = π • d zurück. Die aufgewandte Arbeit ist dann W1 = FU • π • d. Dabei steigt die Mutter um die Gewindesteigung P und übt auf die eingespannten Bauteile die Kraft F2 aus, oder: Abgegebene Arbeit W2 = F2 • P.
Aufgabe: Eine Sechskantschraube M 16 x 1,5 wird mit einem r = d/2 = 200 mm langen Schlüssel angezogen. Die Anzugskraft FU ist 160 N. Mit welcher Kraft F2 wird die Mutter auf die Schraubenverbindung gepresst?
Lösung:
W1 = W2
FU • π • d = F2 • P
F2 = FU • π • d : P = 160 N • π • 400 mm : 1,5 =
F2 = 134 041 N = 134,04 kN; das entspricht einer Hubkraft von etwa 13 Tonnen.