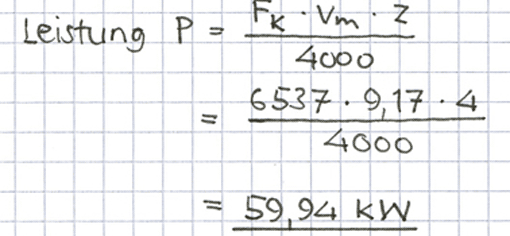Mechanische Leistung (1) 14.03.2009, 12:01
Die Ansichten von Arbeit und Leistung im täglichen Leben stimmen mit den Aussagen der Physik darüber nicht überein. Das erschwert uns die Behandlung des Themas. Aber letzten Endes müssen wir der Physik recht geben - und froh sein an ihren Formeln.
3. Ausbildungsjahr
Mechanische Leistung
oder: Vom Arbeiten schwitzt man nicht
Die Ansichten von Arbeit und Leistung im täglichen Leben stehen im Gegensatz zu den Aussagen der Physik darüber. Das erschwert uns die Behandlung des Themas ein bisschen. Physikalisch ist es z. B. falsch zu behaupten, ein Mensch arbeite gut, wenn er Dinge schnell erledigt. In der mathematischen Formel für Arbeit spielt nämlich die Zeit t keinerlei Rolle. Wahrscheinlich ist es so, dass wir, solange wir nicht die disziplinierende Schulbank drücken, Arbeit und Leistung dauernd durcheinander bringen. Die folgenden Formeln werden es beweisen.
1. Arbeit und Leistung aus geradliniger Bewegung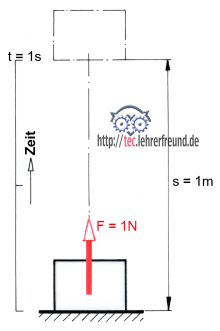
a) Hievt man ein Gewicht F = 1N einen Meter hoch (= s), ohne die Zeit t dafür zu berücksichtigen, dann hat man eine Arbeit verrichtet.
1. Arbeit W = F • s
W = 1 N • 1 m = 1 Nm = 1 Joule = 1 J (Joule, auszusprechen wie dschuhl)
Die Physik behauptet: Es wird keine Arbeit vollbracht, wenn man ein Gewicht F nicht senkrecht nach oben bewegt, sondern waagrecht. Wenn der Lkw vor dem Haus einige Paletten Mauersteine abgeladen hat, könnte ich nach dieser Aussage Tag und Nacht Mauersteine (ihr Gewicht zieht senkrecht nach unten) von der Straße vorne nach hinten in den eben gelegenen Hof schleppen (ich gehe auf einem waagrechten Weg): Ich hätte nichts gearbeitet und folglich wäre mir auch kein Schweiß ausgebrochen.
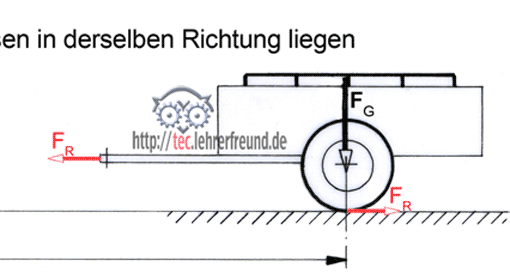
Ich kann es nicht glauben, doch die Theorie bleibt unerbittlich: Arbeit ist nur dann Arbeit, wenn die Kraft und der Weg in derselben Richtung liegen.
Sie muss unerbittlich sein, denn weil gerade der Anhänger im Hof steht, hoffe ich, dieser werde mir das Leben erleichtern. Ich belade ihn mit 250 kg Steinen und ziehe dann. Wieviel Kraft brauche ich, um den Anhänger zu bewegen? Das wissen wir vom Thema Reibung her: Ich muss mit F (= Steingewicht) mal µ (= Reibzahl) ziehen. Ist µ = 0,1, dann muss ich 250 kg mal 0,1, also 25 kg Zugkraft aufwenden. Das ist die Reibkraft, die, weil sie in Fahrtrichtung liegt, die Physik endlich zufrieden stellt.
b) Zurück zu unserem 1-N-Klotz: Hievt man das Gewicht F aber innerhalb einer Sekunde 1 m hoch, dann wurde eine Leistung vollbracht:
2. Leistung P = F • s : t
= 1 N • 1 m : 1 s = 1 Nm/s = 1 Watt = 1 W
1. in 2. eingesetzt –>
3. P = W/t in J/s
In der Formel 2. ist s : t = v = Geschwindigkeit in m/s –>
4. Leistung P = F • v
Dies ist eine Formel, die den Begriff Leistung griffig macht, denn mit den beiden Größen Kraft und Geschwindigkeit sind wir vom tagtäglichen Umgang damit vertraut.
Was kann ein Mensch mit seiner körperlichen Leistungsfähigkeit bewirken? Wie kann ein Fahrzeug, z. B. ein Motorroller, die Leistung ausnützen, die sein Motor hergibt?
Der Mensch kann zwei Größen daraus machen und das gilt auch für Autos, Bagger und Motorroller: Sie können, wie aus der Formel 4. hervor geht, eine Kraft F und eine Geschwindigkeit v daraus machen. Dies ist allerdings nicht beliebig möglich, denn beide finden in der fest installierten Motorleistung ihre Grenzen. Fährt der Motorroller bergauf, dann braucht er offensichtlich viel Kraft; also kann er an der Steigung nicht gleichzeitig eine hohe Geschwindigkeit entwickeln. Fährt er auf ebener Straße, braucht er weniger Kraft und kann dafür schneller fahren.
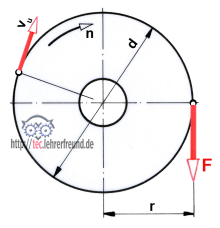
2. Leistung aus einer Drehbewegung
v aus 4. ist die Umfangsgeschwindigkeit vu der Scheibe. Für sie gilt
vu = d • π • n: 60 (in m/s) –> eingesetzt in 4. –>
P = F • d • π • n : 60 = F • 2 • r • π • n : 60 –>
F • r = Drehmoment M –>
P = M • π • n : 30 in Watt ( = Nm/s).
Das Drehmoment sagt etwas über die Kraftwirkung am Scheibenumfang (bei Zahnrädern, Riemenscheiben usw.), die Durchzugskraft (an Antriebsrädern usw.) aus.
In vielen Maschinen sind die Leistungen so hoch, dass man sie in Kilowatt angibt, also:
P = M [Nm] • n [1/s] : 30 • π • 1kW/1000 [Nm/s]. Rechnet man die Konstanten π : 30 : 1000 aus, ergibt sich die Zahl 1/9550, also:
5. P = M • n : 9550 mit
- P in kW
- M in Nm
- n in 1/min oder min-1
3. Leistung und Drehmoment bei Verbrennungsmotoren
P und M bei Verbrennungsmotoren hängen von der Drehzahl eines Motors ab. Die Drehzahl n steht im direkten Zusammenhang mit der Kolbengeschwindigkeit v. Der Kraftstoff im Motor verbrennt nur dann gut, wenn er ausreichend Luft, d.h. Sauerstoff erhält. Bei sehr hohen Motordrehzahlen ist dies aber ein Problem, weil der Sauerstoff bei den schnellen Taktwechseln nicht genügend Zeit hat, nachzuströmen: Der Verbrennungsprozess verschlechtert sich, die Leistung fällt ab.
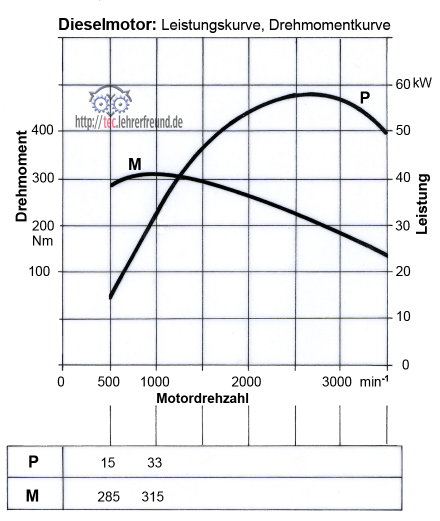
Das folgende Bild zeigt typische P- und M-Verläufe eines Viertakt-Verbrennungsmotors in Abhängigkeit von der Motordrehzahl. Auf diese Verläufe werden wir im nächsten Beitrag näher eingehen.
Anmerkung zur Praxis: Im praktischen Einsatz von Land- und Baumaschinen hat der Drehmomentverlauf eine interessante Auswirkung. Das Drehmoment ist ein Maß für die Durchzugskraft der Räder. Die Nenndrehzahl von Dieselmotoren liegt in der Gegend von 2500 1/min. Muss die Maschine einen erhöhten Widerstand überwinden (z. B. weil der Traktor beim Pflügen in schwereren Boden gerät), dann sinkt bei gleich bleibender Gaspedalstellung die Motordrehzahl und mit ihr die Leistung. Bedenken, der Traktor könne stehen bleiben, sind jedoch unbegründet, weil mit abnehmender Motorleistung - das zeigen die Kurven - das Drehmoment und damit die Kraft an den Rädern ansteigt.
__________________
Rechenübungen zum Thema mit Lösungen finden Sie im Beitrag
Mechanische Leistung (2)