Zeichenübung: Kegel, Zahnrad, Gewinde 26.06.2010, 10:58

Ein im Entwurf gegebenes, unvollständig dargestelltes Bauteil mit Kegel-, Gewinde- und Zahnradelementen soll normgerecht gezeichnet und bemaßt werden.

Zeichnungsübung

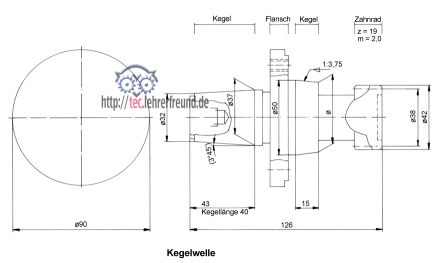
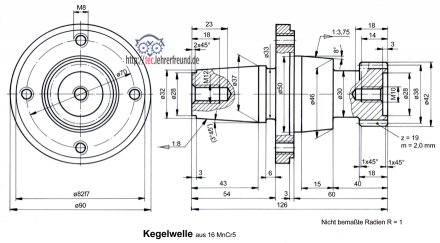
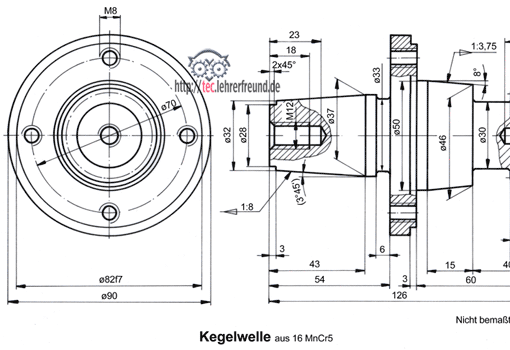
Aufgabe: Zeichnen und bemaßen Sie die unvollständig dargestellte Kegelwelle aus 16 Mn Cr 5. Stellen Sie die Welle im Maßstab 1 : 1 in zwei Ansichten dar nach den folgenden Angaben. 

Gesamtlänge 126 mm; größter Durchmesser 90 mm.

Kegel links: Der Absatz links hat einen Durchmesser 28 mm und ist 3 mm lang. Der größte Kegeldurchmesser endet in einem zylindrischen Auslauf, 5 mm lang. Der Kegel erhält ein Innengewinde M 12 mit 18 mm tiefem nutzbarem Gewinde, Kernbohrung 23 tief, links 2 x 45° angesenkt. Zum Flansch hin ein 6 mm breiter Freistich ø33.

Flansch: In den 12 mm breiten Flansch mit einen Außendurchmesser 90 sitzen auf einem Lochkreis von ø 70 vier gleichmäßig verteilte, durchgehende Gewinde M 8. Der zylindrische Ansatz hat einen Durchmesser 82 mm, Passung f7, und ist 3 mm breit.

Kegel rechts: Das Kegelverhältnis C ist 1 : 3,75. Der zylindrische Teil ø50 ist 5 mm lang. Ein Durchmesser ø 30 verbindet den Kegel mit dem Zahnrad.

Zahnrad: 18 mm breit. Rechts zylindrische Senkung ø 28, 3 mm tief, anschließend zentrisches Innengewinde M 10, nutzbare Länge 14 mm, Kernbohrung 18 mm tief. Der Außendurchmesser ist links und rechts mit 1x45° gebrochen.

1. Berechnen Sie alle fehlenden Angaben zur Bemaßung der beiden Kegel und des Zahnrads.

2. Zeichnen Sie die beiden Ansichten, die Seitenansicht ohne verdeckte Kanten. In der Vorderansicht gibt es die angedeuteten Teilschnitte im Bereich der Innengewinde.

3. Die Übergänge zwischen dem linken Kegel und dem Flansch und dem rechten Kegel und dem Zahnrad sind mit R = 1 abgerundet.

4. Bemaßen Sie das Teil fertigungsgerecht.

Lösungen:

1.

Kegel links

Winkel α/2:  tan α/2 (D – d) : 2 ∙ L = (37 mm – 32 mm) : 2 ∙ 40 mm = 0,0625

α/2 = 3° 45’

Kegelverhältnis C = (D – d) : L = 5 : 40 = 1 : 8

Kegel rechts

Kleiner Durchmesser d:  C = (D – d) : L   –> D – d = C ∙ L   –>
– d = C ∙ L – D (ganze Gleichung dividiert durch (– 1))   –> d = D – C ∙ L = 50 mm – (1 : 3,75 ∙ 15)
d = 46 mm

Winkel α/2:  tan α/2 (D – d) : (2 ∙ L) = (50 mm – 46 mm) : (2 ∙ 15 mm) = 0,13333 –>
α/2 = 8° 

Zahnrad: Teilkreisdurchmesser d = z ∙ m = 19 ∙ 2 mm = 38 mm

Kopfkreisdurchmesser d_a = (z + 2) ∙ m = 21 ∙ 2 mm = 42 mm

4. Fertige Zeichnung