Trigonometrie: Besondere sin-, cos- und tan-Werte 20.06.2016, 06:01
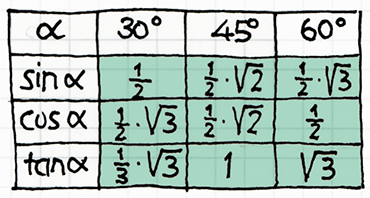
Nur zu wenigen ganzzahligen Winkelwerten gehören übersichtliche Sinus-, Cosinus- und Tangenswerte. Wie sie abgeleitet werden; mit einem praktischen Beispiel.
Trigonometrie
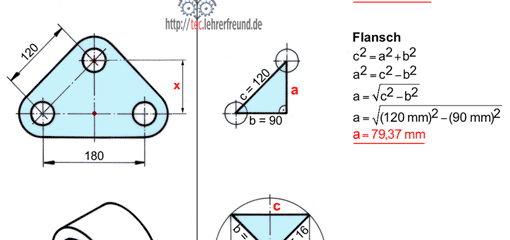
Beim Rechnen mit den Winkelfunktionen Sinus, Cosinus und Tangens erhält man für die Winkel nur ausnahmsweise ganzzahlige Werte. Beispiel: Der Sinus von 20° = sin 20° = 0,342, oder tan 50° = 0,873. Nur zu wenigen ganzzahligen Winkelwerten gehören übersichtliche Sinus-, Cosinus- und Tangenswerte. Diese lassen sich vom gleichseitigen Dreieck ableiten, das durch Einziehen einer Höhe in zwei Hälften aufgeteilt wird (im Bild unten ist es die Höhe a).
Anmerkung: Bei tan 30° steht der Wurzelausdruck im Nenner. Man hätte ihn aber gerne im Zähler; dies geschieht durch Erweiterung es Bruchs mit Wurzel 3. Wurzel 3 mal Wurzel 3 = 3. Dasselbe gilt für sin 45°.

sin 30° = a/2 : a = 1/2
cos 30° = a/2 • √3
tan 30° = a/2 : a/2 • √3 = 1/3 • √3
Vom gleichschenklig-rechtwinkligen Dreieck (zweite Skizze oben) mit den Längen a und s kann man ablesen:
sin 45° = a : √2 = 1/2 • √2
cos 45° = a / a • √2 = 1/2 • √2
tan 45° = a : a = 1
Aufgabe
Nocken, d = 50 mm. Die Nockenscheibe1) (blau gezeichnet) wird auf einen Mitnahmezylinder geschweißt.
Drücken Sie die Kontrolllängen s, t, u und v in der Draufsicht durch d = s aus. s ist im 45°-Dreieck die untere, zwischen den Punkten A und B liegende Kathete.
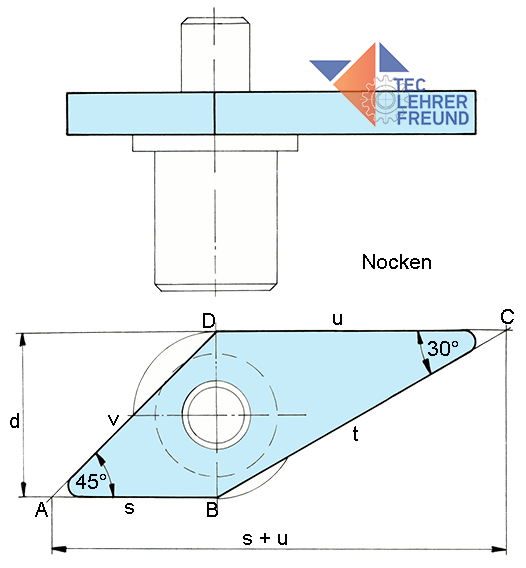
s = d = 50 mm
t ––> sin 30° = d : t ––> t = d : sin 30° = d : 1/2 = d • 2 = 50 mm • 2 =
t = 100 mm
u ––> tan 30° = d : u; u = d : tan 30° = d : (1/3 • √3) = 50 mm : (1/3 • √3)
u = 28,87 mm
v ––> sin 45° = d : v; v = d : sin 45° = 50 mm : (1/2 • √2) =
v = 35,36 mm
s + u = 78,87 mm
___________________
1) Nocken sind im Gesamtzusammenhang eher als Nockenwellen bekannt. Die Nockenwelle ist ein wellenförmiges Maschinenelement, auf dem ein gerundeter Vorsprung in Form einer Scheibe oder eines Zylinders (= der Nocken) sitzt. Die Welle dreht sich um die eigene Achse; durch den auf ihr angebrachten Nocken wird diese Drehbewegung wiederholt in eine kurze Radialbewegung umgewandelt.