Geometrische Grundkonstruktionen (1) 08.11.2013, 06:08
Geometrisch konstruieren heißt, eine vorgegebene Figur mit Zirkel und Lineal exakt darzustellen. In diesem Beitrag wird dies am Beispiel von Geraden und Winkeln gezeigt.
Wir nehmen uns 6 Grundkonstruktionen vor, in denen Gerade und Winkel konstruiert werden sollen.
Die Aufgaben lauten:
1 Finde die Mitte der Strecke A-B
2 Fälle auf die Gerade g ein Lot von Punkt P aus. Das Lot steht senkrecht auf g.
3 Errichte im Anfangspunkt der Geraden g eine Senkrechte
4 Konstruiere zur Geraden g eine durch P gehende Parallele
5 Halbiere den Winkel α
6 Drittle einen rechten Winkel
Aufgabe 1 Finde die Mitte der Strecke A-B
Lösung: Wählen Sie eine Zirkelöffnung > (A-B)/2 = R. Schlagen Sie um A und B den Radius R. Die Verbindung der Radius-Schnittpunkte geht durch die Mitte von A-B.
Aufgabe 2 Fälle auf die Gerade g ein Lot von Punkt P aus
Lösung: Schlagen Sie von P aus einen Radius R. Dieser schneidet die Gerade in zwei Punkten. Schlagen Sie von diesen beiden Schnittpunkten aus wieder Radien R (es können auch größere sein). Die Verbindung zwischen dem auf diese Weise erhaltenen Schnittpunkt und P ist das gesuchte Lot.
Aufgabe 3 Errichte im Anfangspunkt der Geraden g eine Senkrechte
Lösung: Stechen Sie im Anfangspunkt von g die Zirkelspitze ein. Schlagen Sie einen beliebigen Radius R. Lassen Sie R im Zirkel und stechen Sie im Schnittpunkt 1 zwischen g und R ein. Schlagen Sie einen zweiten Radius R. Schlagen Sie um den Schnittpunkt 2 der beiden Radien einen Vollkreis mit dem Radius R. Legen Sie durch die Schnittpunkte 1 und 2 eine schräg nach oben verlaufende Gerade. Durch den Schnittpunkt zwischen Vollkreis und der schrägen Geraden ziehen wir die gesuchte Senkrechte zum Anfangspunkt von g.
Aufgabe 4 Konstruiere zur Geraden g eine durch P gehende Parallele
Lösung: Stechen Sie links auf g die Zirkelspitze ein und ziehen Sie einen durch P gehenden Radius R. Dieser erzeugt auf g einen Schnittpunkt 1. Ziehen Sie zwei weitere Radien R: einen von Schnittpunkt 1 ausgehenden und einen von P ausgehenden. Dadurch entsteht Schnittpunkt 2. Die Gerade durch P und Schnittpunkt 2 ist die gesuchte Parallele.

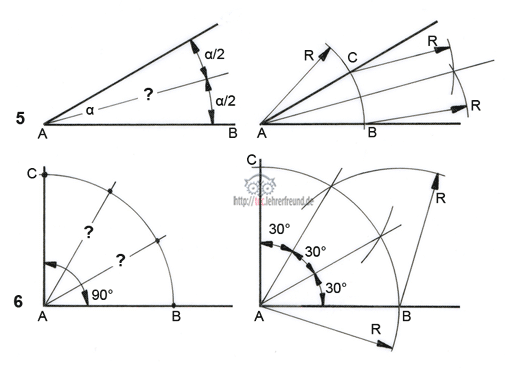
Aufgabe 5 Halbiere den Winkel α
Lösung: Bei A einstechen und einen beliebigen Radius R ziehen. Von den Schnittpunkten B und C aus wieder Radien R schlagen: Die Gerade durch den neuen Schnittpunkt und A ist die gesuchte Winkelhalbierende.
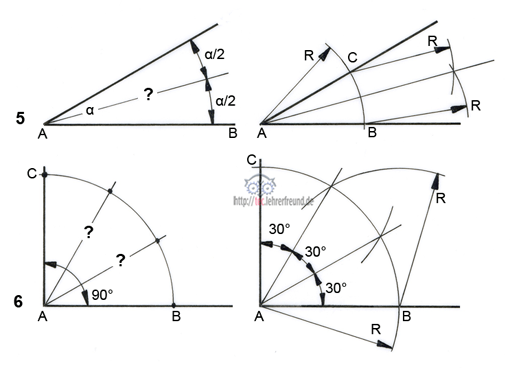
Aufgabe 6 Drittle einen rechten Winkel
Lösung: Bei A einstechen und einen beliebigen Radius R ziehen. Diesen Radius auch von den Schnittpunkten B und C aus schlagen. Die Schnittpunkte mit dem ersten Radius R sind jeweils 30° voneinander entfernt. 3 x 30° = 90°.
Den Aufgaben 3 und 6 liegt jeweils ein gleichseitiges Dreieck zugrunde. Seine Spitzenwinkel sind 60°.