Arbeit (1) 02.04.2009, 10:08
Wir kommen auf den Begriff »Arbeit« zurück. Es gibt Fälle, in denen die Arbeitsformel W = F • s [in W] sehr hilfreich ist. Die »Schiefe Ebene« gehört dazu. Ihr lassen sich Berechnungen an Gewinde- und Keil-Mechanismen zuordnen.
3. Ausbildungsjahr
Arbeit, Schiefe Ebene
Dem Begriff Arbeit scheint, wenn man den Beitrag »Mechanische Leistung (1)« studiert, nur wenig Interessantes abzugewinnen zu sein. Aber es gibt Fälle, in denen die Arbeitsformel W = F • s wirklich hilfreich ist. Besonders die »Schiefe Ebene« gehört dazu.
Gewinde und Keile bestehen aus geneigten Flächen, d. h. Schiefen Ebenen; auch geneigte Straßen oder Abhänge behandelt man unter der Rubrik Schiefe Ebenen.
Beispiel: Wenn eine Last an einen höher gelegenen Ort zu befördern ist, kann man dies auf zweierlei Weise tun: Entweder man nimmt den bequemeren Weg auf der Schräge, oder fährt die Last am Ende der Rampe z. B. per Kran oder Hubstapler hoch.
Wo liegt der Unterschied zwischen den beiden Vorgängen?
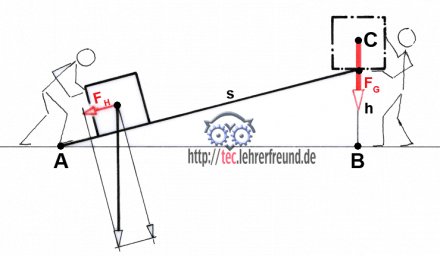
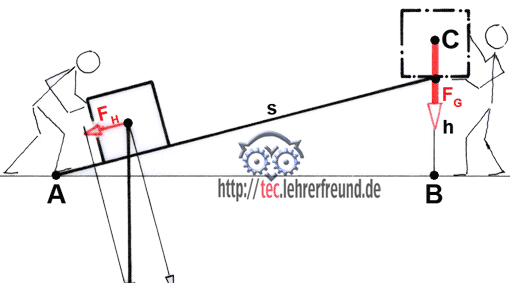
Skizze: Geht man den Weg von A nach C, dann ist er bequem, weil man weniger Kraft braucht; allerdings ist der Weg dann relativ lang. Wählt man den direkten Weg von B nach C, dann muss man die gesamte Last hochstemmen; dafür wird man mit einem kürzeren Weg belohnt. Da man beide Male dasselbe Ergebnis erreicht, hat man in beiden Fällen dieselbe Arbeit verrichtet.
Man könnte auch sagen: Es kommt auf das Gleiche heraus, ob man mit wenig Kraft einen langen Weg zurücklegt oder mit viel Kraft einen kurzen Weg. Dies ist übrigens die Aussage der »Goldenen Regel der Mechanik«.
Damit das Problem etwas verständlicher wird, müssen wir das Kräfteparallelogramm bemühen. Schiebt man die Last von A nach C, muss man die Hangabtriebskraft FH aufwenden. Diese ist umso kleiner, je kleiner der Steigungswinkel ist. Die zu verrichtende Arbeit ist W = FH • s. Kraft und Weg liegen in derselben Richtung.
Hinten an der Rampe ist die Arbeit W2 = FG • h. Wenn aber W1 = W2 ist, dann ist auch FH • s = FG • h
Diese Gleichung lässt sich vier Mal umstellen (Fh = ...; s = ... ; FG = ...; h = ... ?). Versuchen Sie‘s.
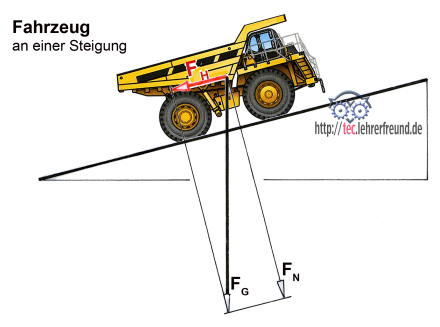
Skizze: Schiefe Ebene und aufwärts fahrender Muldenkipper
Aufgaben
(Bemerkung: In allen folgenden Aufgaben wird die Reibung nicht
berücksichtigt).
Übungsbeispiel: Welche Zugkraft muss ein Lkw auf einer 1 : 8 ansteigenden Straße aufbringen, wenn die zu ziehenden Lasten zusammen 5 Tonnen schwer sind?
Lösung
Steigungsverhältnis 1 : 8 heißt: Bei einer Grundlinie g von 8 m Länge ist der Höhenunterschied h = 1 m. s berechnen wir mit dem Satz des Pythagoras:
s2 = g2 + h2
s2 = 82 + 12 = 65
s = √65 = 8,062 m
FH • h : s = 5000 daN • 1 m : 8,062 m
FH = 620 daN
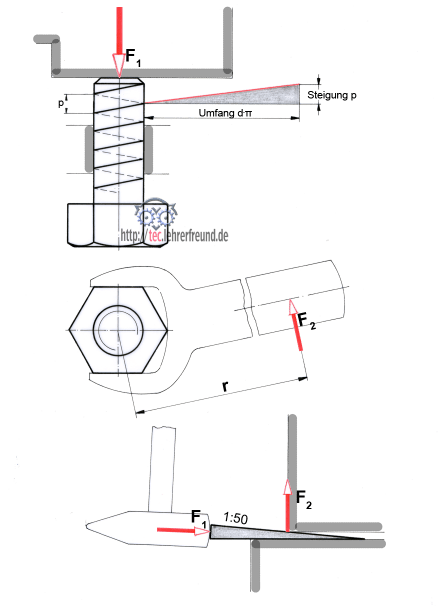
Mit welcher Kraft F1 muss auf den Keil geschlagen werden, wenn damit F2 = 1,5 kN erreicht werden soll? (Verwenden Sie FH • s = FG • h, oder F1 • s = F2 • h –> s : h = 1 : 50)
Lösung F1 = 30 N
Gewinde
Bild: Um eine Last hochzuschrauben, bedient man sich des Gewindes, das ebenfalls eine Schiefe Ebene darstellt. Ein Gewindegang wird aus dem Gewindeumfang U = d • π und der Steigung P gebildet.
Um die Mutter um einen Gang (= P) hochzuheben, muss man mit dem Schraubenschlüssel eine Umdrehung machen (= 2 • r • π)
In den Schraubenschlüssel wird die Arbeit (= W1) »hineingesteckt«, aus der Mutter wird dieselbe Arbeit (= W2) wieder »herausgeholt«, also
W1 = W2
F1 • P = F2 • r • π • 2
F2 = F1 • P : (2 • r • π)
Welche Schlüssel-Handkraft (Schlüssellänge 26 cm) ist an einer M 20-Mutter nötig, wenn ein 10 Tonnen schweres Gewicht angehoben werden soll?
Lösung
M 20 hat eine Steigung P = 2,5 mm;
m = 10 t = 10 000 kg –> F = 10 000 daN
F2 = F1 • P : (2 • r • π)
= 10 000 daN • 2,5 mm : (2 • 260 mm • π)
F2 = 15,3 daN
Welche Steigung P muss ein Gewinde haben, wenn mit einem 12 cm langen Schlüssel und einer Handkraft von 5 N ein Gewicht von 25 daN bewegt werden soll?
Lösung P = 1,5 mm