Das URI-Trio (2) 05.12.2008, 09:09
Das ohmsche Gesetz (U = R • I) beschreibt den Zusammenhang zwischen Spannung, Widerstand und Strom in einem Stromkreis. Wir betrachten Reihen- und Parallelschaltungen und führen Messungen im Stromkreis durch. Berechnungen vertiefen das Thema.
1. Ausbildungsjahr
Reihen- und Parallelschaltung von Widerständen
In der E-Technik kann man Widerstände auf zwei unterschiedliche Arten zusammenschalten:
1. Die Widerstände liegen hintereinander; man sagt dann, sie seien in Reihe geschaltet.
2. Die Widerstände liegen parallel zueinander.
Wo beide Schaltungsarten vorkommen, spricht man von der »gemischten Schaltung«.
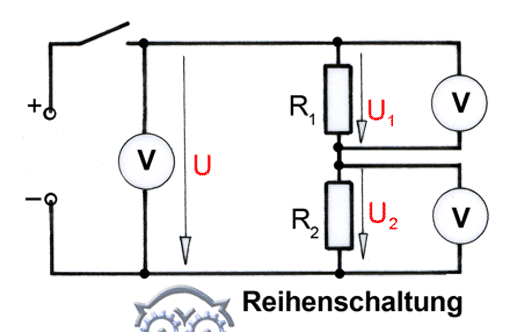
Gesetze der Reihenschaltung
Für die in Reihe (hintereinander) geschalteten Widerstände R1 und R2 gilt (Bild oben):
- Die einzelnen Widerstände summieren sich zum Gesamtwiderstand: Rges = R1 + R2
- Durch alle Widerstände fließt derselbe Strom: I = I1 = I2
- Die angelegte Spannung U teilt sich im Verhältnis der Widerstände in die Teilspannungen U1 und
U2 auf: U = U1 + U2. Am größeren Widerstand liegt die höhere, am kleineren die niedrigere Teilspannung.
Zwei typische Rechenbeispiele
U = 12V, R1 = 400 Ω, R2 = 200 Ω
Rechnung 1: Welcher Strom fließt?
I = U : Rges = 12 V : 600 Ω = 0, 02 A = 20 mA
Rechnung 2: Welche Spannungen fallen an den Widerständen R1 und R2 ab?
U1 = R1 • I = 400 Ω • 0,02 A = 8 V
U2 = R2 • I = 200 Ω • 0,02 A = 4 V
Kontrolle: U = U1 + U2 = 8V + 4V = 12V
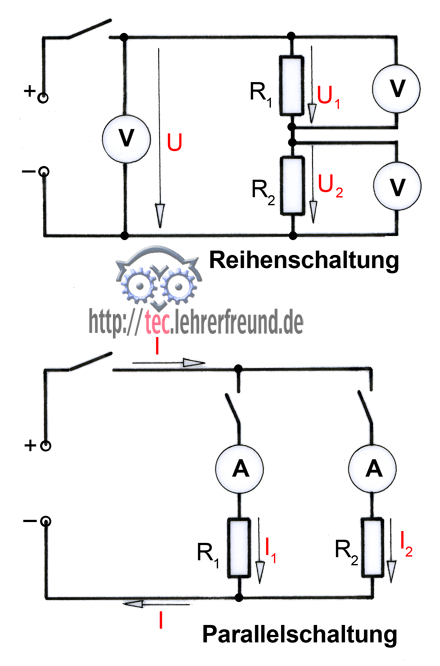
Gesetze der Parallelschaltung
Für die parallel geschalteten Widerstände R1 und R2 gilt:
- An allen Widerständen liegt die gleiche Spannung U = U1 = U2
- Die Teilströme I1 und I2 addieren sich zum Gesamtstrom I = I1 + I2
- Die Teilströme verhalten sich umgekehrt wie die zugehörigen Widerstände: Durch den kleineren Widerstand fließt der größere Strom.
- Je mehr Widerstände die Schaltung besitzt, desto kleiner wird der Gesamtwiderstand und desto größer wird der Gesamtstrom: 1/Rges = 1/R1 + 1/R2+ ...
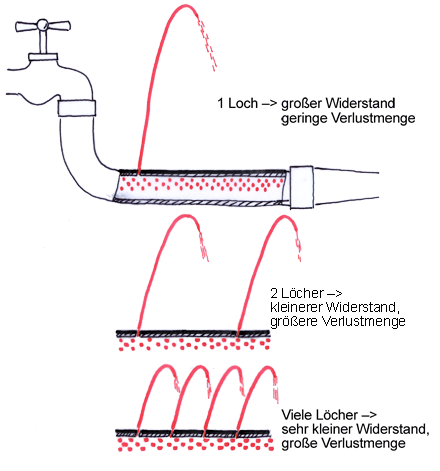
Die Aussage zum Gesamtwiderstand erscheint im ersten Moment zweifelhaft. Zum besseren Verständnis zieht man - wie sehr oft in der Elektrotechnik - Erfahrungen mit dem Wasser heran: Aus einem an einen geöffneten Hahn angeschlossenen Gartenschlauch spritzt Wasser aus einem kleinen Loch. Für den Wasserfluss - er entspricht der elektrischen Stromstärke - ist das kleine Loch ein Widerstand. Würde man ein 2. Loch in den Schlauch stechen, wäre dies einerseits ein weiterer Widerstand, aber insgesamt wäre der dem Wasserdruck entgegenstehende Widerstand geringer geworden. Außerdem hat nun auch die entweichende Wassermenge zugenommen. Je mehr Löcher man in den Schlauch sticht, umso geringer wird der Widerstand und umso mehr Wasser läuft aus dem Schlauch.
Im folgenden Stromkreis sind Widerstände parallel geschaltet.
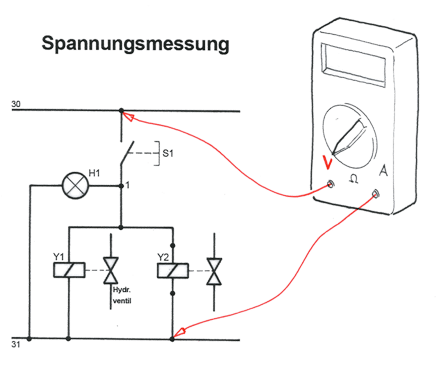
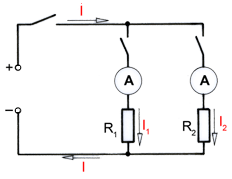
Parallelschaltung; drei typische Rechenbeispiele (Skizze rechts)
U = 12 V, R1 = 400 Ω, R2 = 200 Ω
Rechnung 1: Welche Ströme fließen durch die Widerstände R1 und R2?
I1 = U : R1 = 12 V : 400 Ω = 0,03 A = 30 mA
I2 = U : R2 = 12 V : 200 Ω = 0,06 A = 60 mA
Rechnung 2: Wie groß ist der Gesamtwiderstand der Schaltung?
1/ Rges = 1/400 Ω + 1/200 Ω -> Rges = 133,33 Ω
Rechnung 3: Welcher Gesamtstrom fließt?
I = U : Rges = 12 V :133,33 Ω = 0, 09 A = 90 mA, oder
I = I1 + I2 = 30 mA + 60 mA = 90 mA
Weitere Übungsbeispiele
_________________________________
Nächster Beitrag: Was ist ein NTC-Widerstand?