Kennlinien lesen - kein Hexenwerk (2) 24.04.2009, 10:18

Techniker, besonders aber technische Lehrer, könnten sich ihre Arbeit ohne die Verwendung von Kennlinien nicht vorstellen. Der tec.LEHRERFREUND greift einige Kennlinien heraus und erläutert sie.
2. Kennlinien aus der technischen Praxis
Techniker, auch Techniklehrer natürlich, arbeiten regelmäßig mit Kennlinien, aus denen der tec.LEHRERFREUND einige wenige herausgreift. Ein Teil der Bilder und Grafiken stammt aus dem Internetlexikon WIKIPEDIA.
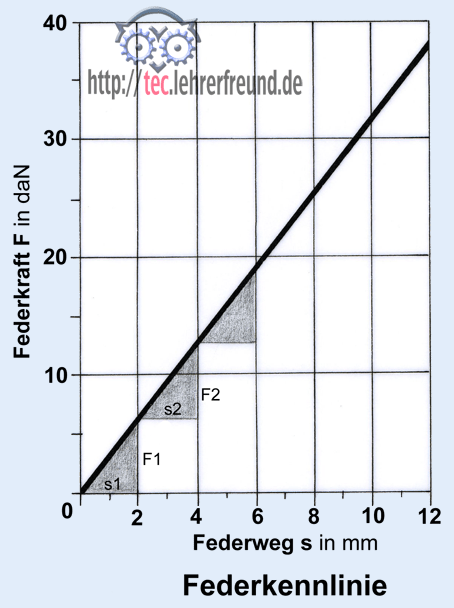
Federkennlinie
Die Federkennlinie stellt die Abhängigkeit der Federkraft F vom Federweg s dar. Ihr proportionaler Verlauf wird auch als »Federkonstante D« bezeichnet. Die geschwärzten Dreiecke im Bild zeigen die Proportionalität der Kennlinie: F1 : s1 = F2 : s2 = ... usw. An jeder Stelle der Kennlinie verlängern 6 daN Federkraft die Feder um 2 mm. Die Federkonstante ist in diesem Fall D = F : s = 60 N : 0,2 cm = 300 N/cm.
Diodenstrom
In WIKIPEDIA ist zu lesen: »Ein Beispiel für eine Kennlinie ist die Abhängigkeit des durch eine Diode fließenden elektrischen Stroms von der elektrischen Spannung. Wird zusätzlich die Temperatur der Diode berücksichtigt, entsteht ein Kennlinienfeld, das aus mehreren, bestimmten Temperaturen zugeordneten Strom-Spannungs-Kennlinien besteht.«
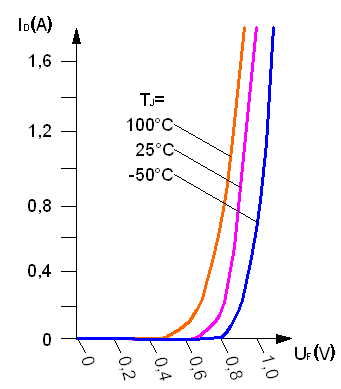
(Bild: Cepheiden: Kennlinie einer Diode bei verschiedenen Temperaturen (Public Domain))
Es geht also um den Strom, der durch eine Diode fließt. Sehen wir uns die mittlere Kennlinie an, bei der die Diode 25°C warm ist. In ihr beginnt erst ab einer Spannung von etwa 0,7 Volt ein Strom zu fließen. Der Strom steigt danach bei geringfügiger Spannungserhöhung sehr stark an: Bei 0,8 V liegt er etwa bei 0,2 A, bei 0,9 V erreicht er schon ca. 1 A.
Erhitzt sich die Diode auf 100°C, dann beginnt sie bei geringeren Spannungen Strom zu leiten. Bei Minustemperaturen dagegen setzt die Stromleitung erst bei 0,8 V angelegter Spannung ein.
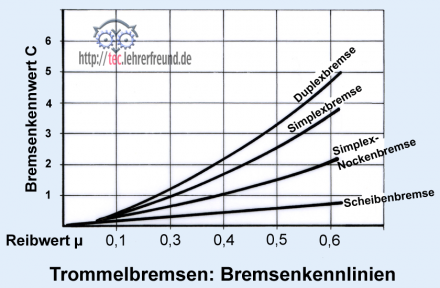
Bremsenkennlinien
Im Rahmen dieses Beitrags geht der tec.LEHRERFREUND davon aus, dass dem Leser Aufbau und Wirkungsweise von Trommel- und Scheibenbremsen geläufig sind. Zur Erinnerung erläutern wir die wichtigsten Eigenschaften kurz. Die Notwendigkeit dieser Beschreibung zeigt ein Weiteres: Viele Kennlinien erfordern ein technisches Hintergrundwissen, ohne welches sie schlecht gedeutet werden können.
Bremsenkennlinien (Bild):
Die Grafik zeigt die Bremsenkennwerte C in Abhängigkeit vom Reibwert µ (mü, griech. Buchstabe). Die Kennlinien der Trommelbremsen haben einen progressiven Verlauf: Mit zunehmendem µ steigen ihre Bremsenkennwerte C stärker an.
C sagt etwas aus über die Selbstverstärkung (= innere Übersetzung der Radbremse) verschiedener Bremsenbauarten. Konkret setzt der Bremsenkennwert C die Umfangskraft an der Trommel zur Spannkraft des Radzylinders ins Verhältnis. C = 2,5 würde heißen: Die Trommelumfangskraft ist 2,5 Mal größer als die Radzylinder-Spannkraft.
Der Reibwert einer Trommelbremse kann erheblich schwanken. Reibwertschwankungen (engl. fading) hängen insbesondere von der Temperatur und der Gleitgeschwindigkeit ab. Diese Empfindlichkeit führte dazu, dass der überwiegende Teil aller Kraftfahrzeuge mit Scheibenbremsen ausgestattet ist, obwohl deren Selbstverstärkung weit unter der von Trommelbremsen liegt (untere Kennlinie).
Insgesamt kann man aus den Kennlinien herauslesen: Je höher der Reibwert zwischen Belag und Trommel ist, desto besser wird die Bremswirkung.
Bemsenbauarten:
a) Simplexbremse (Bild): Sie ist die einfachste Trommelbremse. Zum Spreizen der beiden Bremsbacken dient eine gemeinsame Spannvorrichtung, zum Beispiel ein hydraulischer Zylinder; auch Nocken werden als Spreizelemente eingesetzt. Trotz gleicher Spannkraft an den beiden Bremsbacken erzeugt der linke, der »auflaufende« Backen (Primärbacken) eine höhere Bremskraft als der ablaufende Bremsbacken (Sekundärbacken). Ursache hierfür ist die Selbstverstärkung, die dadurch entsteht, dass der auflaufende Bremsbacken in die Bremstrommel hineingezogen wird. Der ablaufende Backen wird dagegen von der Bremstrommel weggedrückt, weshalb am rechten Backen keine Selbstverstärkung stattfindet.
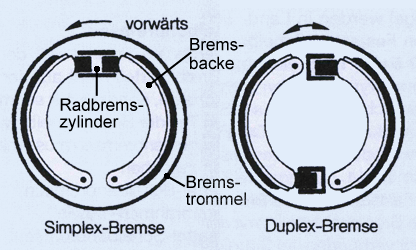
Die Bremsleistung dieser Trommelbremsen-Bauart gilt für die immer schneller und schwerer werdenden Fahrzeuge als nicht mehr ausreichend.
b) Duplexbremse (Bild): Sie hat zwei auflaufende Bremsbacken. Dadurch ist die Bremswirkung in Fahrtrichtung besser als bei der Simplexbremse. Allerdings steht bei Rückwärtsfahrt nur die Bremswirkung von zwei ablaufenden Backen zur Verfügung.
c) Servobremse (kein Bild): Mit dieser Bauart erhält man die beste Bremswirkung. Die Servobremse verfügt bei Vorwärtsfahrt über zwei auflaufende Bremsbacken. Weitere Bremsenbauarten sind die Duo-Duplexbremse und die Duo-Servobremse.
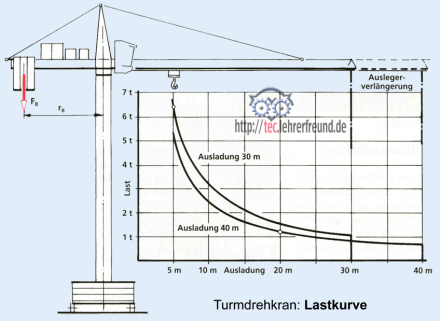
Lastkurve eines Turmdrehkrans
Mit Hilfe der Lastkurve kann man feststellen, wie hoch ein Kranausleger belastet werden kann.
Hier ist die Lastkurve eines Krans mit 30 m Ausladung dargestellt (obere Kennlinie), darunter eine Kurve, die eine Verlängerung des Auslegers berücksichtigt. Wenn diese zweite Kurve tiefer liegt, besagt dies, dass die zulässigen Tragkräfte bei jeweils gleicher Lastposition geringer werden. Der Grund: Der Kran hat wegen des längeren Auslegers ein größeres Eigengewicht beziehungsweise ein größeres Kippmoment, das sich auf die tatsächliche Lastkurve negativ auswirkt.
Zu jeder Auslegerlänge eines Kranes gibt es eine eigene Lastkurve, aus der sich die zulässigen Lasten ablesen lassen.
Wir gehen davon aus, dass wegen der nötigen Kippsicherheit das rechtsdrehende Lastmoment ML 80 % des Ballastmoments MB nicht überschreitet.
Bei Ballastwerten FB = 4 t und rB = 10 m wäre dann ML = 0,8 ⋅ MB = 0,8 ⋅ 4 t ⋅ 10 m = 32 mt (= Metertonnen).
Für den 30-m-Ausleger findet man die Punkte der Lastkurve, indem man die 32 mt durch den jeweiligen Abstand dividiert. Beispiel: Am Abstand rL = 5 m dürfen angreifen: FL = ML: rL = 32 mt : 5 m = 6,4 t; bei 10 m wird FL 3,2 t, usw.
Wird der Ausleger auf 40 m verlängert, dann drückt das zusätzliche Auslegergewicht die Lastkurve nach unten. Bei zusätzlich 300 kg = 0,3 t würde dies vereinfacht auf die halbe Auslegerlänge 20 m gerechnet - ein Moment von 0,3 t ⋅ 20 m = 6 mt ergeben. Bei der 40-m-Kurve bleibt also nur noch ein zulässiges Lastmoment ML von 32 mt - 6 mt = 26 mt übrig. So liegt bei rL = 20 m der Kurvenpunkt bei 26 mt : 20 m = 1,3 t.
Zugversuch
Das Thema wurde bereits in Festigkeitsberechnungen behandelt. Das Bild zeigt das Spannungs-Dehnungs-Diagramm (Spannung = σ, Dehnung = ε)
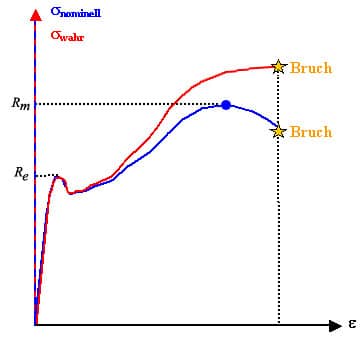
In WIKIPEDIA ist zu lesen: »Die Zugfestigkeit ist die Spannung, die im Zugversuch aus der maximal erreichten Zugkraft bezogen auf den ursprünglichen Querschnitt der Probe errechnet wird. Das Formelzeichen der Zugfestigkeit ist Rm. Dimension der Zugfestigkeit ist Kraft pro Fläche. Häufig verwendete Maßeinheiten sind N/mm² oder MPa (Megapascal). Im Spannungs-Dehnungs-Diagramm kann die Zugfestigkeit aus der maximal erreichten Kraft direkt errechnet werden.
Die aus dem Spannungs-Dehnungs-Diagramm abgelesenen Spannungswerte (Zugfestigkeit, Streckgrenze) entsprechen nicht der wahren Spannung im Material. Dies liegt daran, dass bei der Berechnung der Spannung die Zugkraft auf den Ausgangsquerschnitt bezogen wird.« Der wirkliche Querschnitt der Zugprobe verringert sich aber im Verlauf des Zugversuchs immer mehr; er ist bei höherer Belastung kleiner als der Ausgangsquerschnitt (Querkontraktion, Einschnürung).
Stahl verhält sich beim Auseinanderziehen zunächst elastisch wie eine Zugfeder: Die Zugprobe verlängert sich bis knapp unter den Punkt Re im Verhältnis der Zugkraft, d. h.: doppelte Kraft, doppelte Verlängerung, dreifache Kraft, dreifache Verlängerung, usw. Dies ist ein proportionales Verhalten, das an einem bestimmten Punkt - der Streckgrenze Re - zu Ende ist. Bei weiterer Belastung bricht die Zugprobe sehr schnell. Der höchste erreichte Spannungswert ist die Zugfestigkeit Rm. Beispiel: Die (alte) Stahlkurzbezeichnung St 37 (heute S235JR) besagt: Es handelt sich um einen Stahl, der ab einem Rm = 370 N/mm2 brechen darf.
Zur Kennlinie: Wird die Zugprobe über Re hinaus belastet, beginnt sie sich einzuschnüren, d. h. ihr Querschnitt verringert sich. Die rote Kurve berücksichtigt die Einschnürung. Die blaue Kurve bezieht die Zugbelastung auf den ursprünglichen, also einen gleich bleibenden Querschnitt, weshalb ihre Werte tiefer liegen.
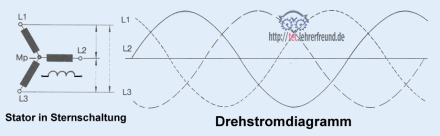
Drehstromgenerator (= Dreiphasenwechselstrom)
Im Bild ist eine Sternschaltung dargestellt, also eine Verknüpfung der drei Wicklungen des Stators in Sternanordnung. Diese Schaltungsart ist bei kleineren und mittleren Drehstromgeneratoren üblich, bei großen ist es eher die Dreieckschaltung.
Durch die Sternschaltung erreicht man eine Erhöhung der effektiven Spannung, die an den Außenleitern L1, L2 und L3 abgenommen werden kann. Bei Kfz-Drehstromgeneratoren wird der Verknüpfungspunkt der Sternschaltung, auch als Mittelpunkt (Mp) bezeichnet, meist nicht heraus geführt und als Anschluss genutzt.
Im Diagramm sieht man die drei verschiedenen Verläufe der im Stator erzeugten Wechselspannungen.
Das Drehstromnetz mit Neutralleiter bietet die Möglichkeit des Anschlusses an zwei verschieden hohe Spannungen.
Im Beitrag »Elektrische Leistung« war von √ 3 die Rede; hier kann die Bedeutung des Faktors nun geklärt werden. Die Effektivwerte der Spannungen zwischen den Außenleitern sind um den Verkettungsfaktor √ 3 (≈ 1,732) größer als die der Spannungen zwischen den Außenleitern und dem Neutralleiter Mp. Entsprechend größer ist bei gleichem Strom die Leistung.
Vertiefenden Aufgaben
1. Federkennlinie.
a) Vorausgesetzt, die oben dargestellte Federkennlinie setze sich über das Schaubild hinaus fort: Welche Kraft wäre für eine Gesamtverlängerung um 1,5 cm nötig?
b) Würde man bei der obigen Kennlinie sagen, die Feder sei »hart«: Wie würde die Kennlinie für ein weichere Feder verlaufen?
(Lösungen:
a) F = D • s = 300 N/cm • 1,5 cm = 450 N = 45 daN
b) Sie würde flacher verlaufen)
2. Diodenkennlinien, Bild oben: Durch eine 25 °C warme Diode fließt ein Strom mit 1,6 A. Welche Spannung liegt an?
(Lösung: ca. 0,97 V)
3. Bremsenkennlinien. Zwischen Bremsbelag und Trommelmantel herrscht ein µ = 0,5. Wie groß ist die Selbstverstärkung C bei einer Duplexbremse?
(Lösung: C = 3,5).
4. Lastkurve Turmdrehkran. Kran mit 30-m-Ausleger. Welche maximale Last kann bei 25 m Hakenabstand angehängt werden?
(Lösung: ca. 1,3 Tonnen)
5. Zugversuch. Wodurch unterscheidet sich die rote von der blauen Diagrammlinie?
(Lösung: Die rote Linie gibt den tatsächlichen Festigkeitsverlauf wieder: Die gemessenen Zugkräfte beziehen sich auf den jeweils eingeschnürten Probenquerschnitt.)
6. Drehstrom, durchgezogene Sinuslinie.
a) Tragen Sie die Drehwinkel an den Schnittpunkten mit der Horizontalen ein. Der erste Schnittpunkt links liege bei Drehwinkel 0°.
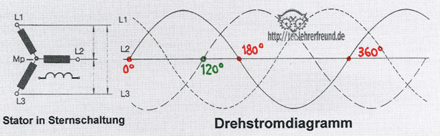
b) Bei welchem Drehwinkel schneidet die langgestrichelte Kurve erstmals die Horizontale?
(Lösung: Bei 120°. Die drei Wechselstromkurven sind um 360°: 3 = 120° zueinander versetzt)