Kennlinien lesen - kein Hexenwerk (1) 17.04.2009, 13:40
Die mathematische Abhängigkeit zweier oder mehrerer physikalisch-technischer Größen zeichnerisch darzustellen, ist in der Technik ein ebenso vorteilhaftes wie beliebtes Verfahren. Im ersten Beitrag eine Übersicht über häufig verwendete Kennlinientypen.
Kurven in der Technik
Die mathematische Abhängigkeit zweier oder mehrerer physikalisch-technischer Größen zeichnerisch darzustellen, ist in der Technik ein ebenso vorteilhaftes wie beliebtes Verfahren. Man könnte mathematische Zusammenhänge auch als Zahlenreihen schreiben, aber man muss es gestehen: Nüchterne Zahlenreihen liefern bei weitem nicht so schnelle und verständliche Informationen wie deren grafische Zusammenfassung. Beweis: Will man sich die Aussagen der Tabelle unten klar machen, erwartet einen harte Arbeit. Schon der Anblick solcher Zahlenkolonnen ist wenig erquicklich.
Auch beim Lesen grafischer Darstellungen gewinnt man nur dann Sicherheit, wenn man es immer wieder übt.
In zwei Beiträgen
- klären wir Grundbegriffe der grafischen Darstellung,
- besprechen wir Kennlinien. Dabei werden wir auf Kennlinien aus verschiedenen Bereichen der Technik eingehen.
1. Grundbegriffe
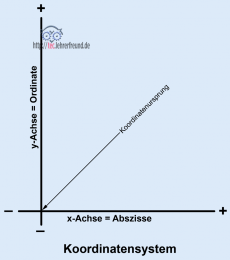
Das Koordinatensystem (auch: Kartesisches Koordinatensystem)
Die Position von Punkten im Raum wird im Koordinatensystem durch Angabe von Zahlenwerten, den Koordinaten, eindeutig bestimmt. Durch mehrere Punkte lassen sich dann bestimmte Objekte (Linien, Abstände, Flächen, Körper) darstellen.
Der Nullpunkt, in dem alle Koordinaten den Wert Null haben, ist der Koordinatenursprung.
Die Achsen
Die beiden senkrecht aufeinander stehenden Geraden (Achsen) haben Namen: Die waagrechte wird häufig x-Achse, die senkrechte y-Achse genannt; die Symbole x und y können auch durch andere ersetzt werden. Die x-Achse wird Abszisse, die y-Achse Ordinate genannt.
Den Achsen ordnet man folgende Vorzeichen zu:
- y-Achse nach oben: +
- x-Achse nach rechts: +
- y-Achse nach unten: –
- x-Achse nach links: –
Die Räume (Quadranten) oben rechts und unten links sind positiv, die anderen beiden sind negativ.
Darstellungsmöglichkeiten
Ein Diagramm ist allgemein eine grafische Darstellung von Daten oder Informationen.
Mathematische oder statistische Diagramme dienen zur Veranschaulichung der Zusammenhänge zwischen zwei oder mehr voneinander abhängigen Werten oder Messgrößen.
Kennlinien
Eine Kennlinie ist Teil eines Diagramms, bezieht sich aber speziell auf Bauteile, Baugruppen oder Geräte. In der Federkennlinie z. B. sind die beiden dargestellten Größen die Kraft F und der Federweg s.
Technische häufig verwendete Diagrammtypen:
Punktdiagramm (kein Bild)
Zwei senkrecht aufeinander stehende Achsen spannen eine Fläche auf, in die die Wertepaare als Punkte (Kreuze, Kreise) eingetragen werden.
Liniendiagramm 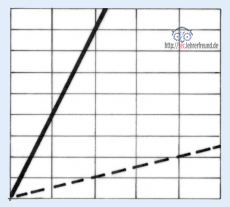
Die Punkte werden miteinander durch Linien (Geraden, Kurven) verbunden. Ist die Fläche zwischen Achse und Linie ausgefüllt, spricht man von einem Flächendiagramm.
Säulendiagramm
Der Abstand zwischen Achse und Datenpunkt wird mit einer senkrecht auf der x-Achse stehenden rechteckigen Fläche dargestellt.
Balkendiagramm
Wie das Säulendiagramm, wobei x- und y-Achse vertauscht sind.
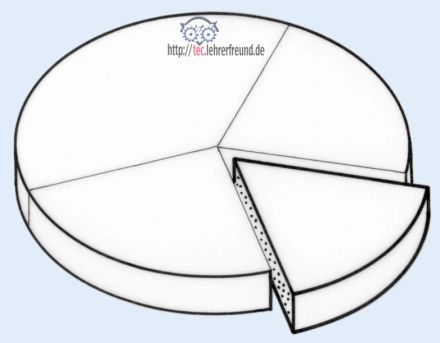
Kreisdiagramm
Sind die Einzelwerte Teile eines Ganzen, dann kann man die Werte in Form von Kreissegmenten zeichnen, um die Größenverhältnisse ihrer Anteile darzustellen. Von einem Tortendiagramm spricht man, wenn der Kreis als perspektivische Scheibe gezeichnet ist.
Netzdiagramm
Bei größeren Datenreihen wird für jeden Wert eine Achse gezeichnet und die Achsen gleichmäßig auf 360° um den Nullpunkt verteilt; die auf den Achsen aufgetragenen und miteinander durch Geraden verbundenen Werte führen zu einer Form, die einem Spinnennetz gleicht, wie beispielsweise die Kurven auf LKW-Tachoscheiben.
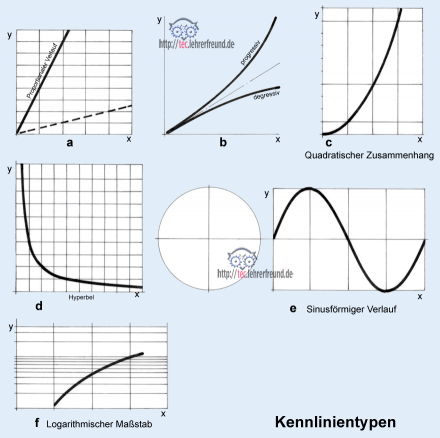
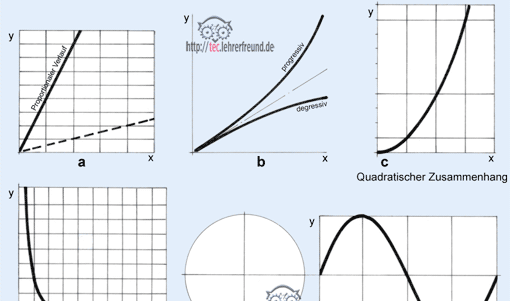
Kennlinientypen
In den Bildern sind aus technischen Systemen bekannte Kurvenformen ausgewählt, die demonstrieren, wie unterschiedlich voneinander die Abhängigkeit der jeweils beiden dargestellten Größen sein kann. Für das bessere Verständnis gehen wir von idealisierten Verläufen aus.
a: Die beiden Größen x und y verhalten sich proportional (z. B. Federkennlinie).
b: Progression, Degression
Von einem proportionalen Verlauf ausgehend spricht man von einem progressiven (sich beschleunigenden) Verlauf, wenn eine Kurve steiler ansteigt als die proportionale Linie; ein degressiver (sich verzögernder) Verlauf ist das Gegenteil: Die Linie steigt weniger langsam an als die proportionale Linie.
c: Hier wurde zum besseren Verständnis der Zusammenhang zwischen Kreis-Durchmesser und Kreisfläche gewählt: A = d2• p : 4. Dieser Zusammenhang ist quadratisch: Wenn sich der Durchmesser verdoppelt (verdreifacht, vervierfacht), dann vervierfacht (verneunfacht, versechzehnfacht) sich die dazugehörige Querschnittsfläche.
d: Der Verlauf ist hyperbolisch. Er entsteht, wenn x und y multipliziert werden, z. B. Q = x • y = p • V (Hydraulik). Je größer x wird desto kleiner wird y. Die Äste der Hyperbel erreichen aber nie eine der beiden Achsen.
e: Bei gleichmäßig sich wiederholenden Vorgängen - meist steckt eine Kreisbewegung, etwa die der Kurbelwelle, des Generators usw. dahinter - ergibt sich eine Sinuslinie.
f: Logarithmischer Maßstab
Bei Verläufen - noch ausgeprägter bei Funktionen - in denen ein noch höherer Exponent als 2 steht, geschieht es schnell, dass die Koordinaten aus Platzgründen nicht mehr vernünftig darstellbar sind. Dann verwendet man nicht den üblichen linearen Maßstab, sondern einen logarithmischen. Dieser zieht die ausufernden Werte zusammen.
(Erläuterung zum Begriff Logarithmus:
Es geht dabei um das Rechnen mit Exponenten. Die Basis dieser Rechenart ist die Zahl 10. 101 = 10; 102 = 100, 103 = 1000 usw. Auf den Achsen einer grafischen Darstellung bedeuten die gleichmäßig auseinander liegenden Zahlen, also die Exponenten 1, 2, 3 usw. 10, 100, 1000 usw., Dabei ist die Distanz zwischen dem Wert 10 und dem Wert 100 dieselbe wie zwischen dem Wert 100 und dem Wert 1000 usw.).
Nächster Beitrag mit Beispielen: Kennlinien (2)