Stirnradgetriebe mehrstufig (2) 02.10.2008, 10:52

Im Beitrag »Stirnradgetriebe mehrstufig (1)« wurde dargelegt, wie man in Getrieben hohe Übersetzungsverhältnisse auf Platz sparende Weise unterbringen kann. Hier führen wir einige Berechnungen an einem solchen Getriebe durch.

3. und 4. Ausbildungsjahr
 

Stirnradgetriebe mehrstufig (2)

Im Beitrag »Stirnradgetriebe mehrstufig (1)« haben wir überlegt, wie man es anstellen muss, wenn man in einem Getriebe ein hohes Übersetzungsverhältnis auf Platz sparende Weise unterbringen will. Hier wollen wir 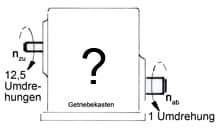Berechnungen an einem solchen Getriebe durchführen.
Überlegen Sie zuerst folgendes: Vor Ihnen liegt ein ausgebautes Getriebe. Sie haben keine Ahnung, wie es im Innern aussieht und wieviele Räder es in diesem Getriebe gibt. Wollten Sie es erfahren, müssten Sie sich die Mühe machen, x Schrauben zu lösen. Sie können mit einem Versuch die Gesamtübersetzung des Getriebes auch ohne Aufschrauben des Getriebekastens herausfinden. Wie?
Sie drehen so oft an der Eingangswelle, bis die Ausgangswelle genau eine Umdrehung gemacht hat. Mussten Sie dafür 12,5 Mal drehen, dann besitzt das Getriebe eine Gesamtübersetzung i_ges = 12,5 : 1 = 12,5. Wie dieses Übersetzungsverhältnis auf die Stufen im (unsichtbaren) Inneren aufgeteilt ist, wissen wir natürlich nicht.

Was Ihnen an solchen Getriebe noch auffallen wird: Die Eingangswelle ist dünner als die Ausgangswelle. Warum das? Weil an der Ausgangswelle eine höhere Drehkraft ( = Drehmoment) herrscht und damit die Welle stärker beansprucht wird. Deshalb muss sie einen größeren Querschnitt besitzen. Versuchen Sie´s: Wenn Ihr Schulkamerad die Ausgangswelle abbremsen will, während Sie am Eingang drehen, wird er gegen Sie nicht ankommen. In ihrer Größe unterscheiden sich die beiden Drehmomente durch das Übersetzungsverhältnis.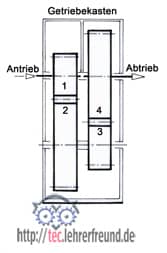

Um die Berechnungsformeln zu entwickeln, sehen wir uns das zweistufige Getriebe rechts an. 

Laut obigem Versuch ist das Gesamtübersetzungsverhältnis

1.  i_ges = n₁ / n₄

2.  i_ges = n₁/n₂ • n₃/n₄. 

3.  Da n₂ = n₃ ->   i_ges = n₁/n₂ •  n₂/n₄

4.  i_ges = n₁ / n₄

Aus Zeile 2. ergibt sich:  i_ges = n₁/n₂ • n₃/n₄

i_ges = i₁ •  i₂; das Gesamtübersetzungsverhältnis ist also das Produkt aus den Einzelübersetzungen.

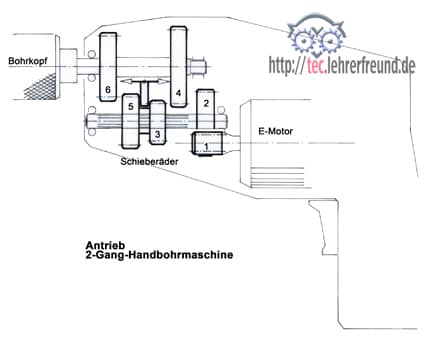
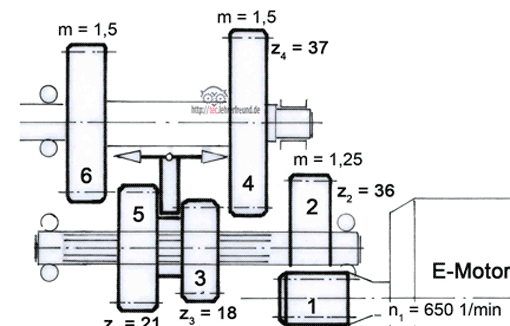
Handbohrmaschine mit zwei Drehzahlen und Leerlaufstellung: Auf der Motorwelle sitzt das Ritzel 1. Es treibt das mit seiner Welle fest verbundene größere Rad 2 an. Die Räder 3 und 5 bilden einen festen Block, der auf der Welle hin- und hergeschoben werden kann. Wird er nach links ins Rad 6 geschoben, erhält man den schnellen Gang. Die Räder 3 und 4 bilden den langsamen Gang.

Angaben zum Getriebe:

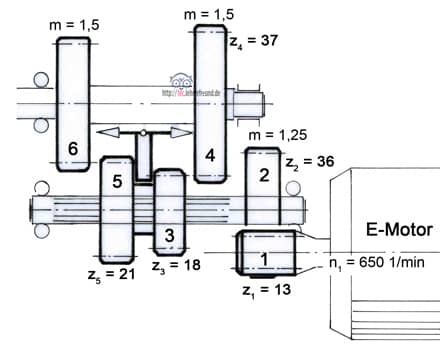
Berechnen Sie: 

1) i_1-2

2) n₂

3) a_1-2

4) a_3-4

5) i_3-4

6) n₄

7) z₆

8) i_5-6

9) n₆

10) d₆

11) d_f6

12) a_5-6