Stirnräder: Einstufiges Getriebe 24.09.2008, 14:47
Wie man einen einstufigen Stirnradtrieb darstellt und berechnet, wird hier beschrieben. Welche Eigenschaften hat ein Zwischenradgetriebe? Wie bestimmt man das Übersetzungsverhältnis?
3. und 4. Ausbildungsjahr
Stirnräder: Darstellung und Berechnung eines Stirnradtriebs
Siehe auch Zahnradberechnungen (1)
1. Mathematik: Berechnungsformeln
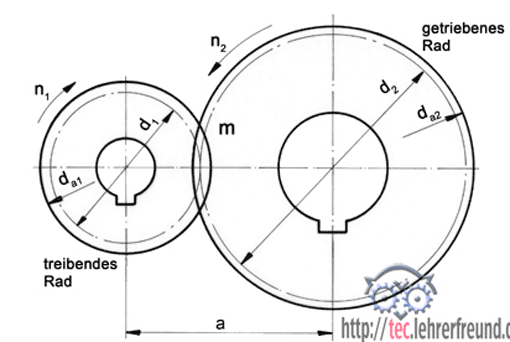
Arbeiten zwei Zahnräder zusammen, (man sagt: Sie »kämmen« miteinander), dann ist durch Norm festgelegt: Das Antriebsrad erhält den Index 1 (also d1, z1, n1), das getriebene Rad 2 (also d2, z2, n2).
d1und d2 sind die Teilkreisdurchmesser, mit denen alle weitergehenden Berechnungen durchgeführt werden. Der Modul m, der ein Maß für die Zahnhöhe ist, ist bei zwei zusammenarbeitenden Zahnräder gleich groß. Die Größe der beiden Räder bestimmt das Übersetzungsverhältnis i. Dieses wird nach Norm in Richtung der Drehzahlen ermittelt:
Übersetzungsverhältnis i = n1/n2 = d2/d1 = z2/z1
Beachten: Bei den Durchmessern und Zähnezahlen steht der Index 2 oben.
Achsabstand a = d1/2 + d2/2 = (m ⋅ z1 + m ⋅ z2) : 2
a = m/2 ⋅ (z1 + z2)
(siehe auch: Mehrstufige Getriebe)
Größe des Übersetzungsverhältnisses
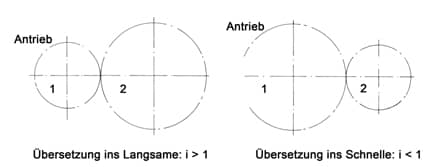
In der Skizze »Einstufiges Stirnradgetriebe« liegt eine Übersetzung ins Langsame vor, d. h. das getriebene Rad macht weniger Umdrehungen als das treibende. n1/n2 ergibt einen Wert, der größer ist als 1,0.
i > 1 -> Übersetzung ins Langsame
i < 1 -> Übersetzung ins Schnelle.
Im Maschinenbau ist die Übersetzung ins Langsame der übliche Fall. Das einem Motor nachgeschaltete Getriebe hat die Aufgabe, die (in der Regel) hohe Motordrehzahl zu reduzieren.
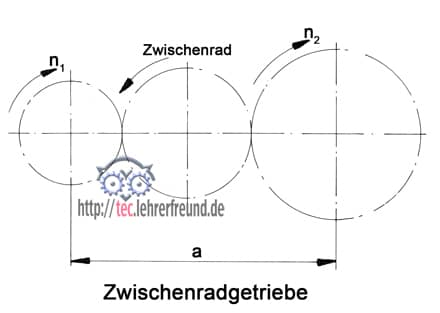
Eine Sonderausführung des einstufigen Stirnradtriebs ist das Zwischenradgetriebe. Bei ihm sitzt zwischen den beiden Rädern 1 und 2 ein weiteres Rad auf einer separaten Welle. Dieses Zwischenrad bewirkt zweierlei:
1. Der Achsabstand wird vergrößert
2. Das getriebene Rad 2 ändert seine Drehrichtung.
Nicht verändert wird das Übersetzungsverhältnis i. (Selbst wenn Sie zehn Zwischenräder einbauen würden: Zwischen An- und Abtrieb bleibt das Übersetzungsverhältnis dasselbe!)
Bei Schaltgetrieben braucht man das Zwischenrad für den Rückwärtsgang.
Beispielrechnung:
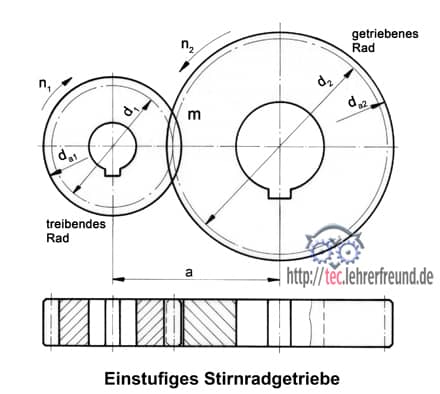
Einstufiges Stirnradgetriebe
z1 = 17 Zähne, z2 = 30, m = 2,5 mm; n1 = 1000 1/min
Berechnen Sie:
a) Übersetzungsverhältnis
b) Achsabstand
c) Abtriebsdrehzahl
d) Den Achsabstand zwischen Rad 1 und Rad 2, wenn das Getriebe ein Zwischenrad mit 23 Zähnen besäße.
2. Schrägverzahnte Stirnräder

Bilden die Zähne einen Winkel zur Zahnradachse, dann spricht man von einer Schrägverzahnung. Schrägverzahnte Räder haben folgende Eigenschaften:
- Sie laufen ruhiger als geradverzahnte Räder
- Sie können größere Kräfte übertragen, weil sie mehr Eingriffsfläche besitzen
- Sie erzeugen eine Axialschubkraft, die von einer entsprechenden Lagerung aufgenommen werden muss.
Bild: Wikipedia: Lüt - Getriebemotor der Firma SEW (CC BY-SA 3.0)
3. Technisches Zeichnen: Darstellung
- Der Kopfkreisdurchmesser wird als breite Volllinie dargestellt
- Der Teilkreisdurchmesser wird als Strichpunktlinie dargestellt; beide Teilkreise berühren sich
- Den Fußkreisdurchmesser zeichnet man in der Regel nicht, wenn aber doch, als gestrichelte Linie
- In der Schnittzeichnung (Seiten- bzw. Draufsicht) wird der Zahn eines Rads gezeichnet. Vom Gegenrad sieht man den Fußkreisdurchmesser und den gestrichelten Kopfkreisdurchmesser
- Die vereinfachte Darstellung eines Zahntriebs begnügt sich mit den Teilkreisen
Lösung der Beispielrechnung
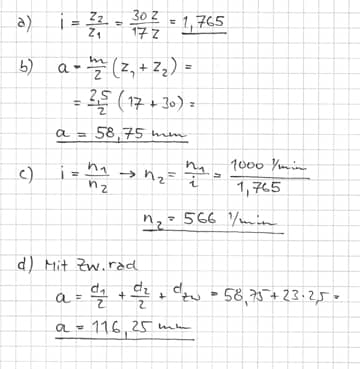
Anmerkung zum Übersetzungsverhältnis i
Wenn die Funktion - z. B. eine präzise Bewegungsübertragung - dem nicht entgegensteht, ergibt sich für das Übersetzungsverhältnis zumeist keine glatte Zahl. Sie entsteht, weil wenigstens ein Zahnrad eine ungerade Zähnezahl erhält. Grund: Beim Kämmen der Zähne sollen diese nicht regelmäßig auf dieselben Gegenzähne treffen. Diese Maßnahme verringert die Abnutzung der Zahnflanken und fördert ein ruhigeres Laufen.