Technische Mathematik: Formeln umstellen (1) 26.03.2010, 10:58
In technischen Berechnungen ist es tägliches Brot, Formeln umzustellen. Übt man dies nicht systematisch, wird sich mancher Schüler die Zähne daran ausbeißen. Eine Anleitung, wie das Umstellen gelingt.
1. Ausbildungsjahr
In technischen Berechnungen ist es eine Routinearbeit, Formeln umzustellen. Übt man dies in der Ausbildung nicht systematisch, wird nicht wenigen Schülern das Thema »Formeln umstellen« ein spanisches Dorf bleiben.
Wenn die gesuchte Größe nicht alleine auf einer (der linken) Seite steht, dann muss sie schrittweise isoliert und dorthin gebracht werden.
Beispiel: Gestreckte Länge eines aus Stahl gebogenen Winkels. Er wird in einzelne, auf der neutralen Faser gemessenen Längen aufgeteilt.
L = l1 + l2 + l3. Diese Formel soll nach l3 umgestellt werden.
Wie bei allen Gleichungen gilt auch hier die wichtige Regel:
Wird eine der beiden Seiten verändert, dann muss dies (gleichzeitig) auch auf der anderen Seite geschehen.
Man kann diese Regel mit dem Wiegen auf einer Balkenwaage vergleichen: Die Formel muss wie die Waage im Gleichgewicht bleiben. Bei der Waage ist dies nur möglich, wenn jeweils beide Schalen mit denselben Gewichten be- oder entlastet werden.
Die Veränderung wird als Anweisung rechts von der Formel vermerkt.
Beispiel: Gestreckte Länge eines Winkelstahls
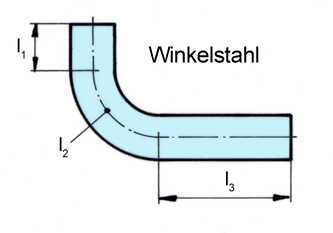
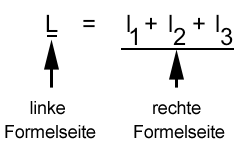
L = l1 + l2 + l3 ∣ – (l1 + l2) = Anweisung: Subtraktion, auf beiden Seiten durchzuführen.
L – (l1 + l2) = l1 + l2 + l3 – (l1 + l2); damit heben sich rechts l1 und l2 auf:
L – l1 – l2 = l3 –> l3 muss nach links gebracht werden; die Seitenvertauschung ändert nichts an der Gleichung:
l3 = L – l1 – l2
So könnte man bei der Behandlung des Themas im Unterricht vorgehen: Man sucht Formeltypen heraus und behandelt diese nacheinander in Zweierschritten:
1. Formeltyp vorstellen, nach unbekannter Größe umstellen.
2. Schüler mit anderen Formeln desselben Typs üben lassen.
Formeltypen sind:
Formeln mit Summen/Differenzen
Formeln mit Produkten
Formeln mit Brüchen
Formeln mit Summen und Produkten
Formeln mit Potenzen/Wurzeln
Umstellungsbeispiele
Formeln mit Produkten
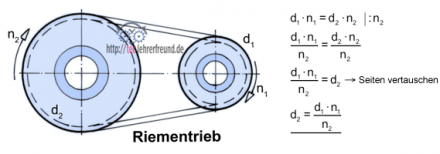
Beispiel Riementrieb (siehe Beitrag Riementrieb Berechnung)
d1 • n1 = d2 • n2 –> umstellen nach d2
Formeln mit Brüchen
Beispiel Dreiecksfläche
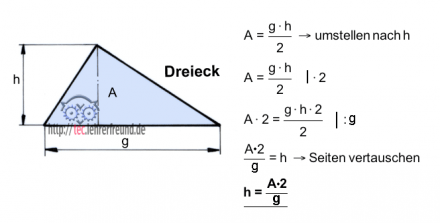
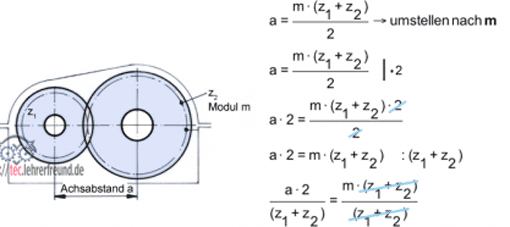
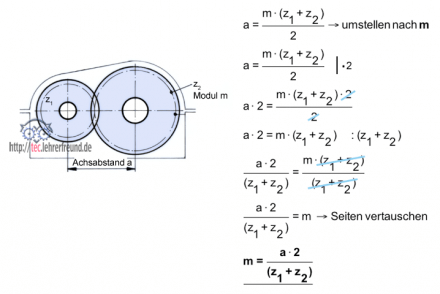
Beispiel Zahntrieb (siehe Beitrag Stirnräder)
Achsabstand, Modul, Zähnezahl
Blaue Schrägstriche: Diese Größen kürzen sich schrittweise heraus.
Formeln mit Summen und Produkten
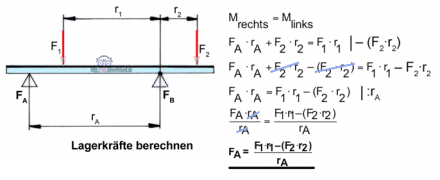
Beispiel Lagerbelastung
Formel umstellen nach FA
Formeln mit Summen und Produkten
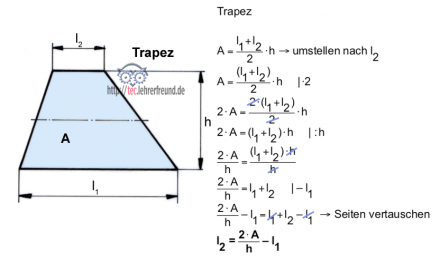
Beispiel Trapezfläche
Formel A = ... umstellen nach l2
Formeln mit Potenzen und Wurzeln
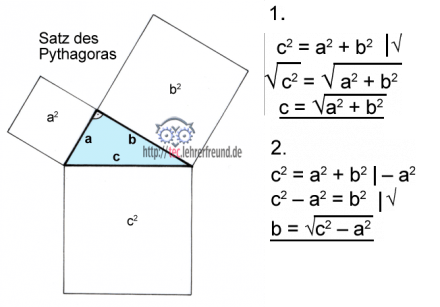
Beispiel Satz des Pythagoras
c2 = a2 + b2
1. Formel nach c umstellen
2. Formel nach b umstellen
Formeln mit Potenzen/Wurzeln
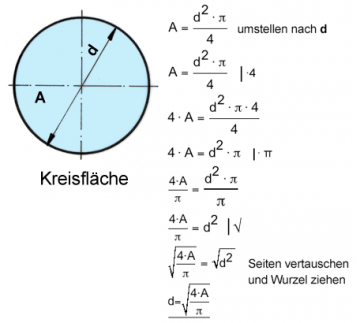
Beispiel Kreisfläche
Formel A = ... umstellen nach d
______________
Im nächsten Beitrag vertiefen wir das Umstellen von Formeln