Verbrennungsmotor (3): Hubraum, Verdichtungsverhältnis 04.01.2010, 12:55
Bei Berechnungen zum Verbrennungsraum sind Hubraum, Hub-Bohrungs-Verhältnis und Verdichtungsverhältnis Schlüsselbegriffe. Sie werden erläutert und mit Rechenbeispielen untermauert.
Berechnungen am Motor
1. Hubraum
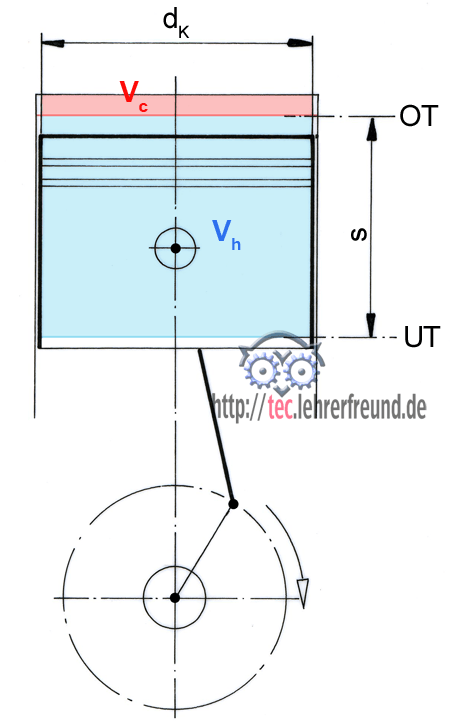
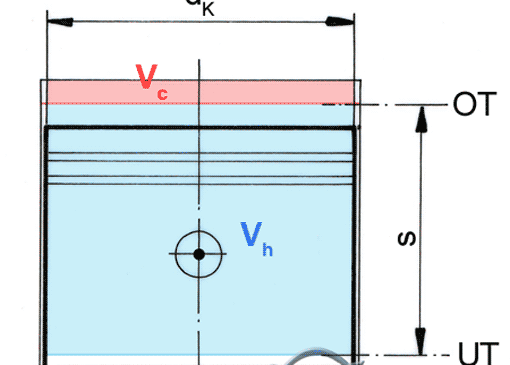
Bild: Der Zylinderraum besteht aus dem Hubraum Vh und dem Verdichtungsraum Vc. Das Verdichtungsverhältnis ε (epsilon) gibt an, wieviel mal größer der Zylinderraum ist als der Verdichtungsraum. Ist zum Beispiel ε = 7 : 1, dann ist der Zylinderraum sieben Mal größer als der Verdichtungsraum (siehe weiter unten).
Beim Hin- und Hergehen des Kolbens ändert sich jeweils am oberen und am unteren Wendepunkt seine Bewegungsrichtung. Diese Umkehrpunkte sind der obere und untere Totpunkt (OT und UT).
Weil die Kolbenfläche eine Kreisfläche ist, ist der Hubraum ein zylindrisches Volumen mit den Rechengrößen: Zylinderbohrungsmesser d in cm, Kolbenhub s in cm. Daraus ergibt sich die Rechenformel:
Zylinderhubraum = Zylinderquerschnitt mal Hub oder
Fo 1: Vh = A • s (cm3)
Wird für den Querschnitt A = d2 • π/4 in die Formel eingesetzt, dann ist der Zylinderhubraum:
Fo 2: Vh = d2 • π/4 • s (cm3)
Die Maßeinheiten für den Hubraum sind: cm3 oder dm3 (1 dm3 = 1l (Liter)).
Beachten: Der Bohrungsdurchmesser d und der Hub s werden in mm angegeben; vor dem Einsetzen in die Rechenformel müssen sie in die gewünschte Maßeinheit cm oder dm umgerechnet werden.
Aus dem Zylinderhubraum lassen sich sowohl der Hub s wie auch der Bohrungsdurchmesser d berechnen. Dazu muss die Hubraumformel nach der gesuchten Größe umgestellt werden:
Fo 3 und Fo 4:
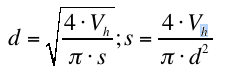
Bei mehrzylindrigen Motoren ergibt sich der Gesamthubraum des Motors VH aus dem Zylinderhubraum Vh multipliziert mit der Anzahl der Zylinder z, also (Fo 5):
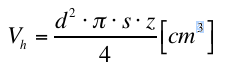
2. Hub-Bohrung- Verhältnis
Für die Gestaltung des Verbrennungsraums findet man in der Praxis drei verschiedene Möglichkeiten: Der vorgegebene Hubraum eines Motors kann entweder mit einer großen Zylinderbohrung und einem kleinen Hub (Kurzhuber) erreicht werden; wenn Hub und Bohrung gleich groß sind, spricht an von einem Quadrathuber. Schließlich ist die Kombination kleiner Bohrungsdurchmesser und großer Hub (Langhuber) möglich. Jede der drei verschiedenen Bauarten hat ihre Vor- und Nachteile. Das Verhältnis zwischen Motorbohrung und Hub wird als Hub-Bohrung-Verhältnis α bezeichnet.
Fo 6: α = s : d
Das Hub-Bohrung-Verhältnis ist - wie alle Verhältniszahlen - dimensionslos.
3. Verdichtungsverhältnis
Der Zylinderraum besteht aus dem Hubraum Vh und dem Verdichtungsraum Vc. Die angesaugte Luft (Dieselmotor) oder das angesaugte Kraftstoff-Luft-Gemisch (Ottomotor) wird im Verdichtungstakt auf das Volumen des Verdichtungsraums zusammengedrückt, wenn der Kolben den oberen Totpunkt erreicht hat.
Verdichtungsverhältnis ε = (Vh+Vc) : Vc
oder Fo 7:
ε = (Vh: Vc) + 1
Darin sind:
ε = Verdichtungsverhältnis
Vh = Zylinderhubraum (cm3)
Vc = Verdichtungsraum (cm3)
Rechenbeispiele:
1. Wie groß ist der Zylinderhubraum Vh (in cm3) eines Traktormotors, dessen Bohrungsdurchmesser d =114 mm bei einem Hub von s = 122 mm beträgt?
2. Der Zylinderhubraum eines 4-Zylinders VH = 1032 cm3. Wie groß ist der Bohrungsdurchmesser bei einem Hub von 72 mm?
3. Die Zylinder eines Sechszylindermotors haben Bohrungsdurchmesser 106 mm und einen Hub von s = 125 mm. Wie groß ist der Gesamthubraum in Liter?
4. Wie groß ist das Verdichtungsverhältnis eines Ottomotors mit einem Zylinderhubraum von Vh = 470 cm3 und einem Verdichtungsraum von Vc= 58 cm3?
5. Ein Zylinder mit einem Bohrungsdurchmesser 120 mm besitzt ein Hub-Bohrung-Verhältnis 1,1333. Wie groß ist der Hub?
6. Ein Ottomotor hat ein Vh = 230 cm3 und ein ε = 7,5:1. Wie groß ist der Verdichtungsraum?
Lösungen
1. Vh = A • s = d2 • π/4 • s = (11,4 cm)2 • π/4 • 12,2 cm =
Vh = 1245,26 cm3
2. Vh = VH : 4 = 1032 cm3: 4 = 258 cm3
Vh = d2 • π/4 • s –> d siehe Formel Fo 3 –> d = 67,55 mm
3. In dm rechnen, um Liter zu erhalten:
VH = d2 • π/4 • s • z = (1,06 dm)2 • π/4 • 1,25 dm • 6 =
VH = 6,619 l
4. ε = (Vh: Vc) + 1 = (470 cm3: 58 cm3) + 1 = 9,1 = 9,1 : 1
5. α = s : d –> s = d • α = 120 mm • 1,133 = 136 mm
6. ε = (Vh: Vc) + 1 –>
Vc = Vh : (ε – 1) = 230 cm3 : 6,5
Vc= 35,38 cm3