Flächenschwerpunkt 02.02.2010, 12:35

Wie ermittelt man den Schwerpunkt eines flachen Körpers? Hier leistet die Drehmomentengleichung nützliche Dienste.

Schwerpunkte bestimmen

In der klassischen Mechanik versteht man unter dem Schwerpunkt den Punkt, an dem die Masse des Körpers die gleiche Wirkung auf andere Körper hätte, wenn sie in diesem einzigen Punkt vereint wäre.
Besteht ein Körper aus einem Material mit durchgängig gleicher Dichte, dann entspricht sein Massenmittelpunkt dem geometrischen Volumenschwerpunkt. Anders gesagt: Der Punkt, in dem wir einen Körper, eine Fläche oder ein Liniengebilde abstützen oder aufhängen müssten, damit sie in jeder beliebigen Lage stehen bleiben, heißt Schwerpunkt.
Symmetrielinien und Symmetrieebenen gehen durch den Schwerpunkt.

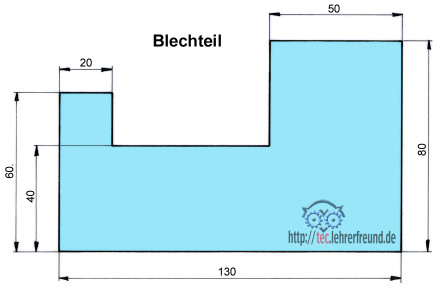
Wo liegt der Schwerpunkt des gezeichneten, u-förmigen Blechteils?

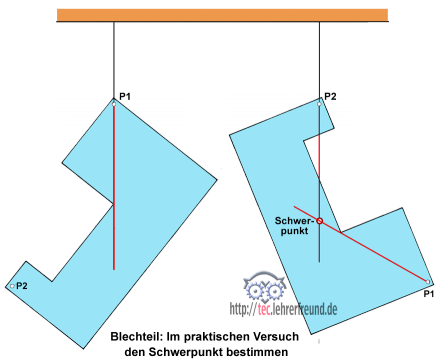
Mit einem Versuch kann man den Schwerpunkt praktisch bestimmen: Man hängt das Blechteil an zwei beliebigen Punkten (hier P1 und P2) auf und verlängert jedesmal den senkrechten Faden (rote Linien) nach unten. Im Schnittpunkt der beiden Linien liegt der Schwerpunkt des Körpers (Skizze rechts). Die Rechenmethode sowie eine zeichnerische Konstruktion dazu werden weiter unten beschrieben. 

Welche weiteren Möglichkeiten der Schwerpunktbestimmung gibt es?
Der Schwerpunkt ist der Angriffspunkt der resultierenden Masse des Körpers. Wir finden ihn, indem wir nach den Gesetzen der Statik die Wirklinien der Resultierenden der Teilmassen bzw. Teilgewichte F 1, F 2 usw. für zwei Körperlagen bestimmen. Da es sich um Parallelkräfte handelt, brauchen wir
- rechnerisch den Momentensatz für zwei gewählte, senkrecht aufeinander stehende Hilfsachsen,
- zeichnerisch das Seileckverfahren, ebenfalls für zwei Achsen.

Hat der Körper, die Fläche oder das Liniengebilde eine Symmetrielinie, so liegt der Schwerpunkt darauf. Zur Lösung ist dann nur eine Achse senkrecht zur Symmetrielinie erforderlich.
 

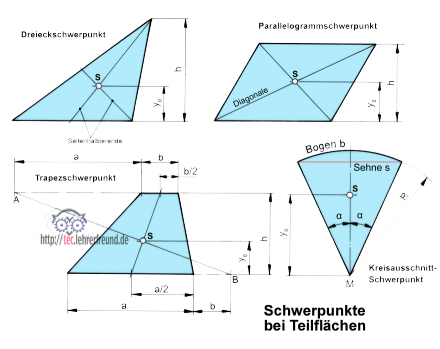
Flächenschwerpunkte

Einige ausgewählte Flächen:

a) Dreieck

Der Schwerpunkt der Dreiecksfläche liegt im Schnittpunkt der Seitenhalbierenden.
Schwerpunktabstand y₀ = h/3

b) Parallelogramm

Der Schwerpunkt des Parallelogramms liegt im Schnittpunkt der Diagonalen. Das gilt auch für Quadrat, Rechteck, Rhombus und Rhomboid, ebenso für den Parallelogrammumfang.

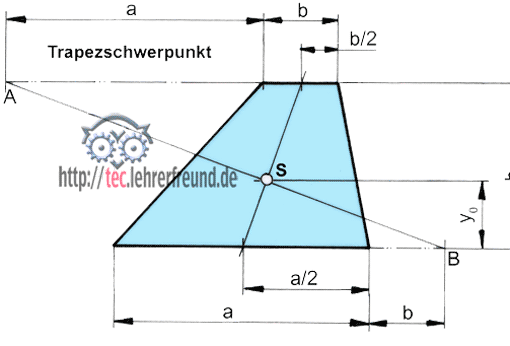
c) Trapez

Wir tragen an Seite a die Seite b an und an Seite b die Seite a. Damit können wir die Strecke AB zeichnen. Nun verbinden wir die Mitten der Seiten a und b (a/2 und b/2) miteinander. Der Schnittpunkt ergibt den Flächenschwerpunkt.

d) Kreisausschnitt
Es sind:
R = Kreisradius,
2α° = Zentriwinkel,
b = Bogenlänge = 2α° ⋅ R: 57,3
s = Sehnenlänge = 2 ⋅  R ⋅  sinα

Schwerpunktabstand y₀ = 2/3 ⋅ R ⋅ s : b
____________________

Etwas komplizierter wird’s bei zusammengesetzten Flächen: Darauf geht der tec.LEHRERFREUND in einem der nächsten Beiträge ein. Im nächsten Beitrag wird das Seileckverfahren erläutert.