Dynamik (2): Dynamisches Gleichgewicht 03.09.2014, 15:20

Bei Berechnungen zum dynamischen Gleichgewicht muss immer auch die Trägheitskraft berücksichtigt werden. Erläuterungen und Rechenaufgabe.

Dynamisches Gleichgewicht

Zur Statik und zur Dynamik hatten wir im vorangehenden Beitrag zwei Aussagen formuliert: 
Die Statik ist das Teilgebiet der Mechanik, das sich mit dem Gleichgewicht von Kräften an ruhenden Körpern befasst. 
Die Dynamik ist das Teilgebiet der Mechanik, das die Bewegung von Körpern/Massen unter dem Einfluss von Kräften beschreibt. 

Beispiel Stahlträger. Er ist im Gleichgewicht, wenn die ihn belastenden Kräfte und die Stützkräfte gleich groß sind und gegensinnig wirken. Damit heben sie sich auf und der Träger ist im statischen Gleichgewicht.  

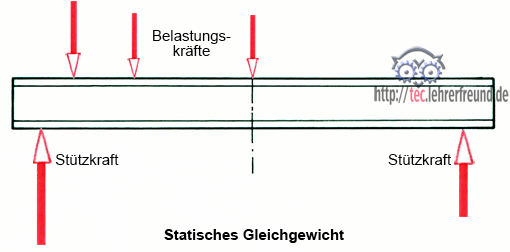
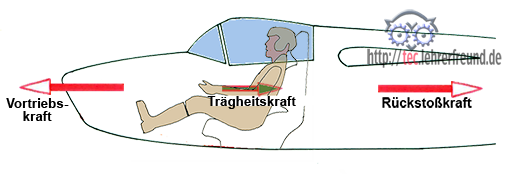
Gleichgewicht herrscht auch am beschleunigt oder verzögert bewegten Körper, wenn alle an ihm wirkenden Kräfte sich aufheben. Dann spricht man vom dynamischen Gleichgewicht. Ein Beispiel dafür wäre ein startendes oder landendes Flugzeug.

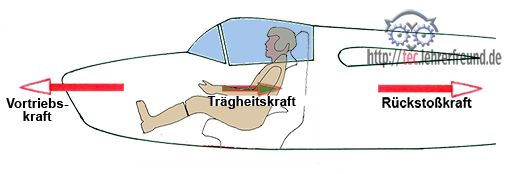
In der Berechnungsformel des dynamischen Gleichgewichts erscheint immer die Trägheitskraft F_T. Sie wirkt der Beschleunigungsrichtung entgegen: F_T = m • a.
Die Gleichgewichtsbedingung heißt:
ΣX = 0, oder:
+F_V – F_R – F_T = 0. 
Setzt man für die Trägheitskraft F_T = m • a ein, erhält man
+ F_V – F_R – m • a = 0, oder
Vortriebskraft F_V = F_R + m • a, d. h. die Vortriebskraft F_V ist gleich der Rückstoßkraft F_R plus dem Trägheitswiderstand F_T. 

Wir fassen zusammen: Durch die Einführung der Trägheitskraft F_T = m • a als Gegenkraft können Trieb- und Bremsaufgaben als Gleichgewichtsaufgaben gelöst werden. Auf diese Weise vereinfacht sich eine Dynamikaufgabe zur Statikaufgabe. 

Bild unten: Kräfte an einer sich beschleunigenden Rakete. Die Größe des Trägheitswiderstands hängt von der Raketenmasse und dem Beschleunigungswert ab.

Rechenbeispiel

Die Seiltrommel soll eine Last F_L = F_G nach oben ziehen und dabei beschleunigen. m_L = 800 kg; a = 0,24 m/s². 

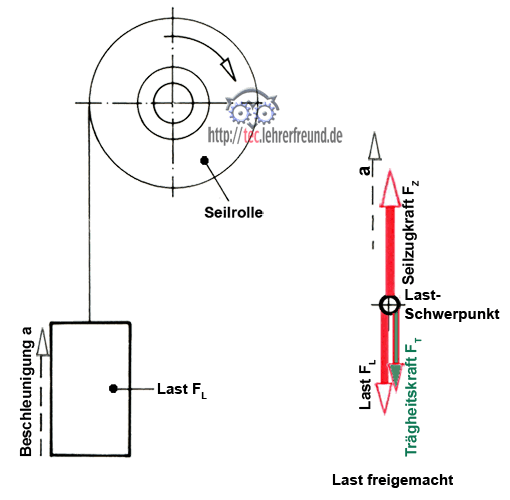
Lösung: 
Wir vereinfachen in unserer Skizze die Last zu einem kleinen Kreis und zeichnen die wirksamen Kräfte F_L, F_Z und F_T ein (oben). 

Gleichgewichtsbedingung:

+ F_Z – F_L – FT = 0; F_T = m • a 

+ FZ – F_L – m • a = 0 

Auf der Erde wirkt auf alle Körper das durch die Schwerkraft bestimmte Gewicht F_G, und mit ihm die Erdbeschleunigung (= Fallbeschleunigung) g = 9,81 m/s². Daraus ergibt sich für F_G = m • g = 800 kg • 9,81 m/s² = 7 848 N. m = F_G : g setzen wir in die vorige Formel ein: 

+ F_Z – F_L – F_G : g • a = 0. Weil F_L = F_G, finden wir:

F_Z = F_G + F_G : g • a = F_G • ( 1 + a : g ); Zahlen eingesetzt: 

F_Z = 7 848 N • ( 1 + 0,24 m/s² : 9,81 m/s²) = 7 848 N • 1,024 

F_Z = 8 036 N 

Information aus: Beschleunigte und verzögerte Bewegungen

Es gibt kaum eine Bewegung, die nicht durch eine Beschleunigung eingeleitet und durch Verzögerung wieder zum Stillstand gebracht wird. Dies ist besonders dort augenfällig, wo hohe Geschwindigkeiten üblich sind, wie etwa beim Fliegen. Um 800 km/h zu erreichen ist eine lange Beschleunigung erforderlich. Bei der Rückkehr zur Landegeschwindigkeit muss kräftig verzögert werden.   
Das Kennzeichen der beschleunigten oder verzögerten Bewegung ist die Zu- oder Abnahme der Geschwindigkeit v. 

Bezeichnungen:
Geschwindigkeit v in m/s 
Beschleunigung, Verzögerung a in m/s²                                     
Beschleunigungszeit, Verzögerungszeit t in  s 
Beschleunigungsweg, Verzögerungsweg s in m 

Berechnungsformeln: 

Beschleunigung oder Verzögerung

1. a = v : t 

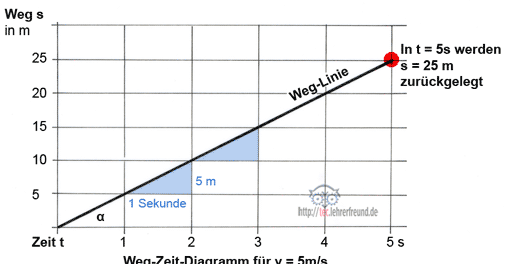
Beschleunigungs- oder Verzögerungsweg s:

s = v • t : 2 

Setzt man aus 1. für v = a • t, dann ist

s = a • t² : 2. Setzt man aus 1. für t = v : a, dann ist der

Verzögerungsweg s = v² : 2 • a 

Aufgabe Förderkorb

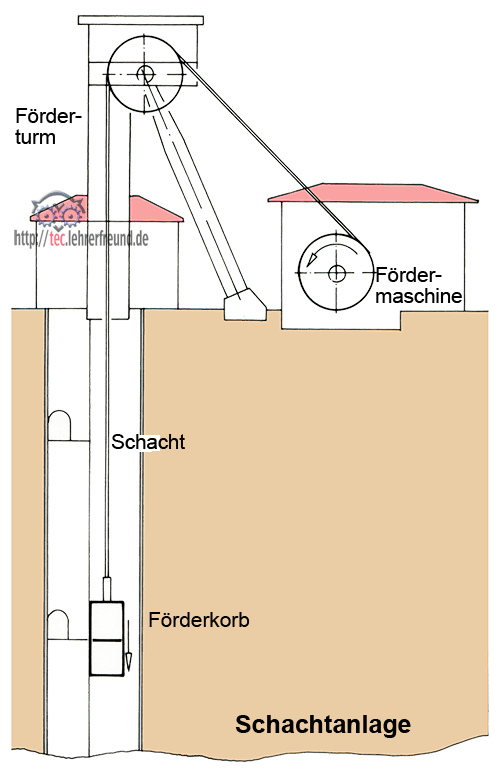
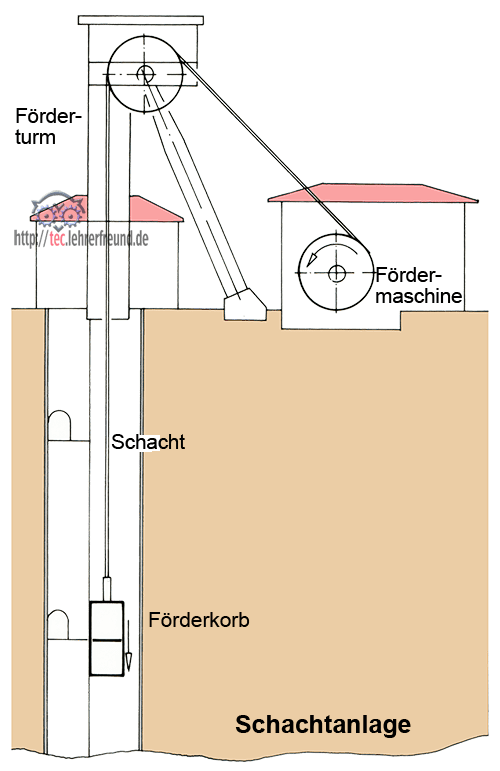
Ein Förderkorb, Masse 5 t, fährt mit 8 m/s gleichförmig abwärts in den 240 m tiefen Schacht. Am Ende wird seine Fahrt verzögert und er kommt während der letzten 25 m zum Stehen. Welche Kraft F_Z wirkt an der Aufhängung des Seils am Förderkorb? 
Anmerkung: Bergwerke unter Tage werden meist durch senkrechte Schächte von der Erdoberfläche aus erschlossen. Als Transportmittel für Personen und Material dient der Förderkorb, eine robuste Aufzugskabine. Sie hängt im Schacht an einem Seil und wird von einer Fördermaschine über die Seilrolle im Förderturm auf- und abwärts bewegt.

Lösungsvorschlag: 

Aus dem 
Verzögerungsweg s = v² : 2 • a rechnen wir
Verzögerungswert a = v² : 2 • s = (8 m/s)² : 2 • 25 m = 1,28 m/s²
Dynamisches Gleichgewicht

+F_Z – F_G – F_T = 0 

F_G = m • g = 5 000 kg • 9,81 m/s2 = 49 050 N • m = F_G : g setzen wir in die vorige Formel ein: 

F_Z = F_G + m • a

F_Z = F_G + F_G : g • a = F_G • (1 + a : g); Zahlen eingesetzt 

F_Z = 49 050 N • (1 + 1,28 m/s² : 9,81 m/s²) = 49 050 N • 1,13 =   

F_Z = 55 426,5 N