Gleichbleibende und beschleunigte Bewegungen (1) 22.04.2012, 07:09
Eine Bewegung kann geradlinig oder kreisförmig sein, ihre Geschwindigkeit konstant (gleichbleibend) oder beschleunigt bzw. verzögert. Zum besseren Verständnis benutzt man häufig gut verständliche Diagramme: das Weg-Zeit-Diagramm (s-t-Diagramm) und das Geschwindigkeits-Zeit-Diagramm (v-t-Diagramm). Mit Berechnungsbeispielen.
Bewegungen
1. Gleichbleibende Bewegungen
Eine Bewegung kann geradlinig oder kreisförmig sein, ihre Geschwindigkeit konstant (gleichbleibend) oder beschleunigt bzw. verzögert.
Gleichbleibende, geradlinige Bewegungen
In vielen Bereichen der Technik achtet man auf gleichbleibende Geschwindigkeiten. Beispiele: Bearbeitung von Werkstücken, Vorschubgeschwindigkeiten, Betrieb von Transportbändern. Dabei werden in gleichen Zeitabständen jeweils gleiche Wege zurückgelegt. Die Geschwindigkeit v ist der in einer Zeiteinheit t zurückgelegte Weg s. Sie bleibt über die gesamte Bewegung konstant.
Bezeichnungen:
Geschwindigkeit v in m/s
Weg s in m
Zeit t in s
Zwei häufig benutzte und gut verständliche Diagramme zu Darstellung der Geschwindigkeit sind das Weg-Zeit-Diagramm (s-t-Diagramm) und das v-t-Diagramm. Überhaupt ist es vorteilhaft, Bewegungsabläufe bildlich darzustellen. Schwierigere Aufgaben lassen sich auf diese Weise leichter überschauen und lösen.
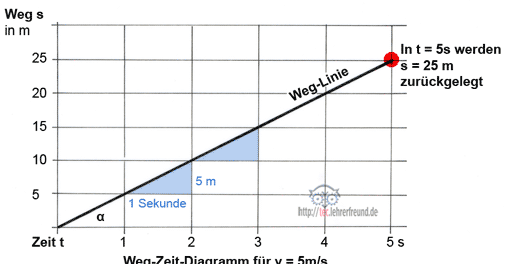
Zur Erläuterung wird hier die Bewegung eines Körpers mit einer Geschwindigkeit v = 5 m/s betrachtet. Die Weg-Linie im Weg-Zeit-Diagramm ist eine ansteigende Gerade, denn bei gleichförmiger Bewegung in gleichen Zeitabschnitten werden gleiche Wege zurückgelegt; hier sind es in jeder Sekunde 5 Meter. Die Größe der Geschwindigkeit ist durch die Neigung (der Tangens) der Geraden bestimmt:
Geschwindigkeit v = s : t = tan α = konstant.
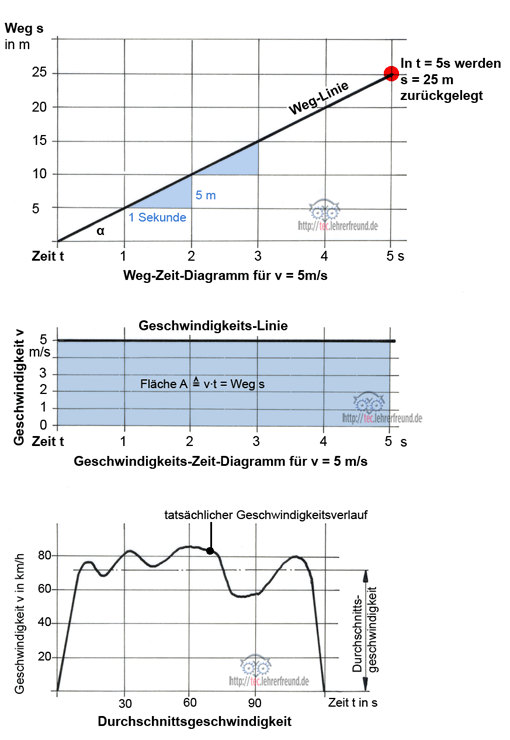
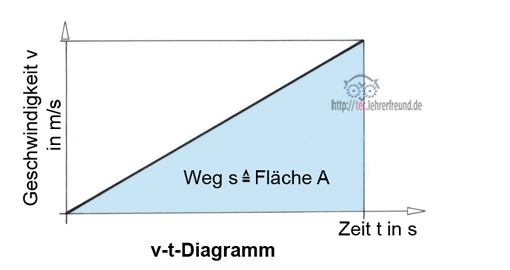
Ebenso wichtig ist das Geschwindigkeits-Zeit-Diagramm. Die Geschwindigkeits-Linie im v-t-Diagramm ist eine waagerechte Gerade, weil bei gleichförmiger Geschwindigkeit v = konstant ist.
Der von 0 bis zur Zeit t zurückgelegte Weg s entspricht der Fläche unterhalb der v-Linie.
Weg s = Fläche A = v · t
Aus diesem Grunde wird das v-t-Diagramm vornehmlich bei zusammengesetzten Bewegungen verwendet. Dort kann man die Bewegungsvorgänge und die zurückgelegten Wege klar erkennen und berechnen.
Durchschnittsgeschwindigkeit
Oft haben Bewegungsabläufe keine konstante Geschwindigkeit. Sie sind beschleunigt oder verzögert. Ein Beispiel dafür ist das Autofahren. Hier begnügt man sich meist damit, die Bewegung als konstant anzunehmen und mit einer Durchschnittsgeschwindigkeit zu rechnen.
2. Beschleunigte und verzögerte Bewegungen
Es gibt kaum eine Bewegung, die nicht durch eine Beschleunigung eingeleitet und durch Verzögerung wieder zum Stillstand gebracht wird. Dies ist besonders dort augenfällig, wo hohe Geschwindigkeiten üblich sind, wie etwa beim Fliegen. Um 800 km/h zu erreichen ist eine lange Beschleunigung erforderlich. Bei der Rückkehr zur Landegeschwindigkeit muss kräftig verzögert werden.
Das Geschwindigkeit-Zeit-Schaubild unten zeigt Fahrabläufe eines Busses. Während der Beschleunigungszeit von 5 Sekunden nimmt seine Geschwindigkeit in gleichen Zeitabschnitten um den gleichen Betrag bis auf 40 km/h zu. Nach weiteren 35 Sekunden beginnt er zu bremsen; nach 7 s Bremszeit bleibt der Bus stehen.
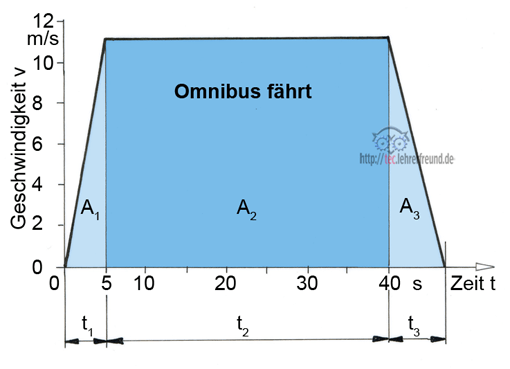
Das Kennzeichen der beschleunigten oder verzögerten Bewegung ist die Zu- oder Abnahme der Geschwindigkeit v.
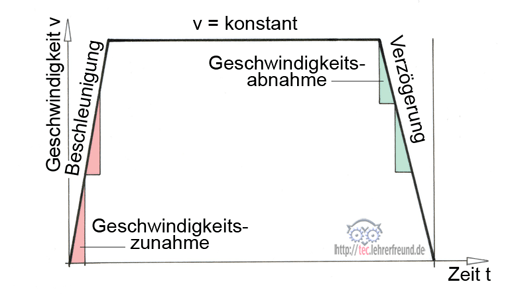
Bezeichnungen:
Geschwindigkeit v in m/s
Beschleunigung, Verzögerung a in m/s2
Beschleunigungszeit, Verzögerungszeit t in s
Beschleunigungsweg, Verzögerungsweg s in m
(Δ ist der griechische Buchstabe »delta«. Er wird zur Kennzeichnung einer Änderung — hier Geschwindigkeitsänderung — benutzt. Wir setzen ihn nur dort ein, wo das Verständnis es erfordert.)
Die zurückgelegte Wegstrecke ist das Flächenstück unterhalb der v-Linie.
Merke: Ein Körper bewegt sich dann gleichmäßig beschleunigt oder verzögert, wenn seine Geschwindigkeit v gleichmäßig zu- oder abnimmt!
Berechnungsformeln:
Beschleunigung oder Verzögerung
a = v : t
Beschleunigungs- oder Verzögerungsweg s:
s entspricht der blauen Fläche :
s = v · t : 2
Setzt man für v = a · t, dann ist
s = a · t2 : 2
Setzt man für t = v : a, dann ist
s = v2 : 2 · a
________________
Aufgaben
Aufgabe 1
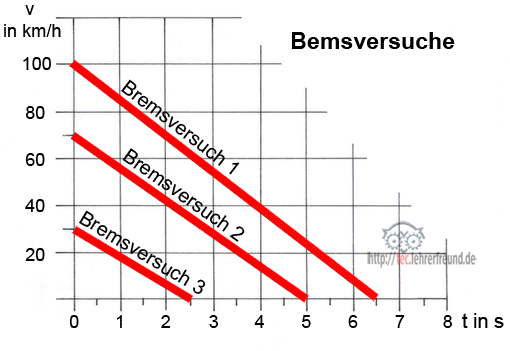
Bremsversuche an Motorrädern: Drei Abbremsversuche werden in einer Grafik festgehalten. Lesen Sie die Werte aus der Grafik heraus und berechnen Sie damit die Bremswege s1, s2 und s3.
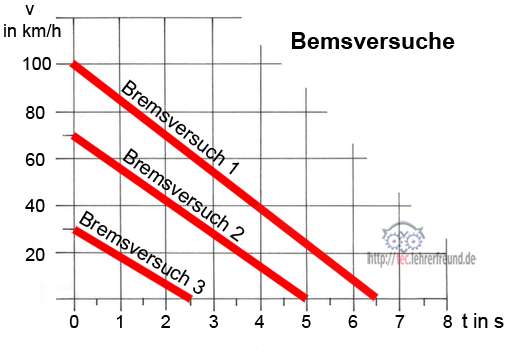
Aufgabe 2
Eine S-Bahn erreicht nach dem Anfahren und einer Fahrstrecke von 120 m eine Geschwindigkeit von v = 60 km/h. Welche Zeit benötigt sie dafür?
Aufgabe 3
Ein Omnibus kommt in 5 Sekunden auf 40 km/h, fährt dann 40 Sekunden mit dieser Geschwindigkeit und bremst 7 Sekunden lang bis zum Stillstand. Welchen Weg hat er zurückgelegt?
Aufgabe 4
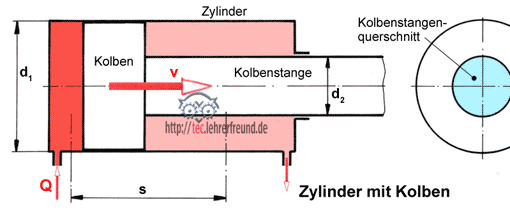
Ein Hydraulikkolben fährt mit 18 m/min ein. Mit einer Verzögerung a = 2,2 m/s2 soll er auf Null abgebremst werden.
Berechnen Sie Verzögerungsweg und Verzögerungszeit.
Aufgabe 5
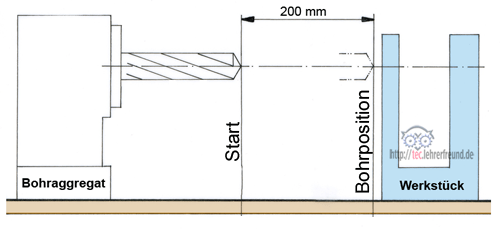
Bohraggregat. Die Skizze zeigt den Bewegungsablauf beim Eilgang zwischen Startbeginn und Bohrbeginn. Angaben:
- Start, Beschleunigung auf Eilganggeschwindigkeit v = 0,12 m/s
- Gleichbleibende Eilganggeschwindigkeit v = 0,12 m/s
- Abbremsen auf Null bis zur Bohrposition, danach Bohrbeginn.
Die Beschleunigung und Verzögerung sind jeweils 1,5 m/s2.
Wieviel Zeit vergeht zwischen Start und Abbremsen auf Null? Erläutern Sie den Rechenweg mit Skizzen.