Rechnungen zu gleichbleibenden und beschleunigten Bewegungen (2) 26.04.2012, 06:13

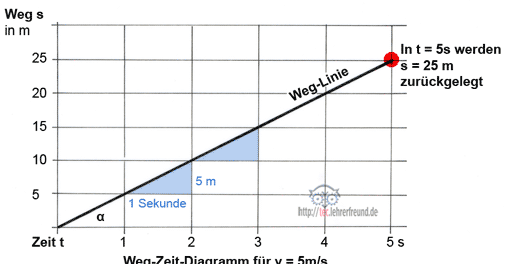
Eine Bewegung kann geradlinig oder kreisförmig sein, ihre Geschwindigkeit konstant (gleichbleibend) oder beschleunigt bzw. verzögert. Zum besseren Verständnis benutzt man häufig das Weg-Zeit-Diagramm (s-t-Diagramm) und das v-t-Diagramm. Lösung der Berechnungsbeispiele aus Teil 1.

Aufgaben

Zuerst wollen wir auf eine Umrechnung hinweisen, die bei Geschwindigkeitsberechnungen sehr häufig verlangt wird: Es ist die Umrechnung von km/h in m/s und umgekehrt. 

Es ist: 1 km / h = 1000 m : 3600 s, also
1 km/h = 1 m : 3,6 s, 
oder 
1 m/s = 3,6 km/h. 
__________________________

Lösungen 

Aufgabe 1:

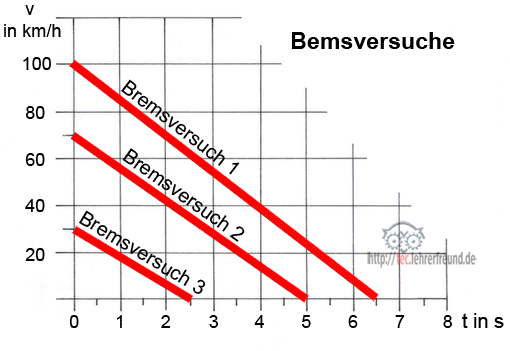
Bremsversuche an Motorrädern

Drei Abbremsversuche werden in einer Grafik festgehalten. Lesen Sie die Werte aus der Grafik heraus und berechnen Sie damit die Bremswege s₁, s₂ und s₃. 

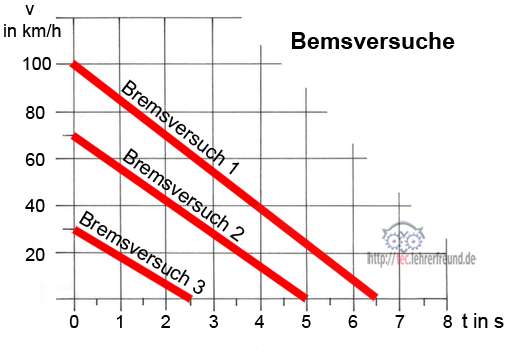
Versuch 1: 

Gegeben: v₁ = 100 km/h; t₁ = 6,5 s 

Gesucht: s₁

Lösungen:

Beschleunigungs- und Verzögerungsaufgaben rechnen wir stets mit den Einheiten m und s. 100 km/h sind 100: 3,6 = 27,78 m/s

s₁ = v₁ : 2 · t₁  = 27,78 m/s : 2 · 6,5 s =

s₁ = 90,3 m 

s₂ = 48,6 m

s₃ = 10,4 m 

Aufgabe 2: 

Eine S-Bahn erreicht nach dem Anfahren und einer Fahrstrecke von120 m eine Geschwindigkeit von v = 60 km/h. Welche Zeit benötigt sie dafür?  

Geg.: s = 120 m; v = 60 : 3,6 = 16,67 m/s

Ges.:  t  

s = v : 2 · t –> t = 2 · s : v 

t = 2 · s : v 

t = 2 · s : v = 120 m : 16,67 m/s 

t = 14,4 s

Aufgabe 3

Ein Omnibus kommt in 5 Sekunden auf 40 km/h, fährt dann 40 Sekunden mit dieser Geschwindigkeit und bremst 7 Sekunden lang bis zum Stillstand. Welchen Weg hat er zurückgelegt?

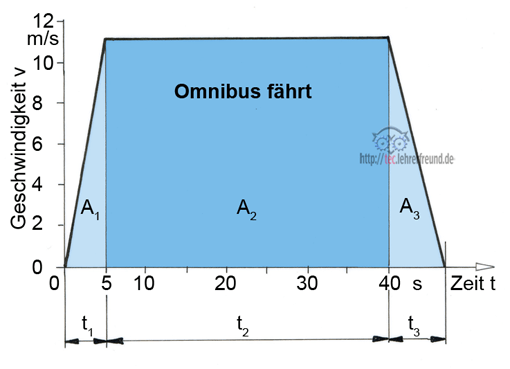
Lösungsansatz: Die Fläche des Trapezes im v-t-Diagramm entspricht dem Fahrtweg s. 

Gesamtfahrtweg s = s1 + s2 + s3 

s₁ = v · t : 2 = 11,11 m/s : 2 · 5 s = 27,8 m 

s₂ = 444,4 m 

s₃ = 38,9 m

s = 511,1 m

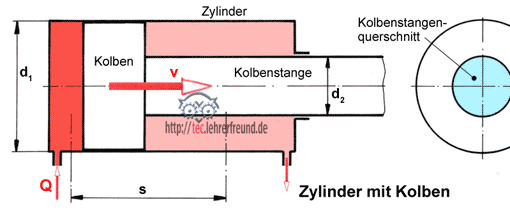
Aufgabe 4

Ein Hydraulikkolben fährt mit 18 m/min ein. Mit einer Verzögerung a = 1,2 m/s² soll er auf Null abgebremst werden.
Berechnen Sie Verzögerungsweg und Verzögerungszeit. 

Geg: a = 1,2 m/s²; v = 15 m/min = 15 : 60 = 0,25 m/s

Ges.:  a) s;    b) t 

a) s = v² : 2 : a = (0,25 m/s)² : 2 : 1,2 m/s² =

     s = 0,026 m 

b) aus s = a · t² : 2 –> t = √ s · 2 : a = √ 0,026 m · 2 : 2,2 m/s²

      t = 0,024 s

Aufgabe 5

Bohraggregat. Die Skizze zeigt den Bewegungsablauf beim Eilgang zwischen Startbeginn und Bohrbeginn. Angaben:

- Start, Beschleunigung auf Eilganggeschwindigkeit v = 0,12 m/s
- Gleichbleibende Eilganggeschwindigkeit v = 0,12 m/s
- Abbremsen auf Null bis zur Bohrposition, danach Bohrbeginn.

Die Beschleunigung und Verzögerung sind jeweils 1,5 m/s².

Wieviel Zeit vergeht zwischen Start und Abbremsen auf Null? Erläutern Sie den Rechenweg mit Skizzen.

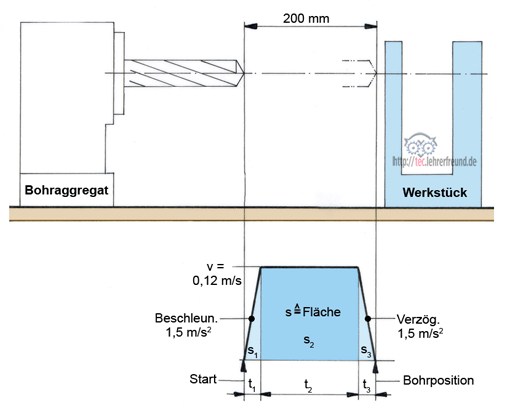
Lösungsansatz: Die Fläche des Trapezes im v-t-Diagramm entspricht dem Eilgangweg s.  

s₁ + s₃ = v · t : 2 · 2 = v · t_1,3
s₁ + s₃ = 0,12 m/s · t_1,3
s₂ ist eine konstante Geschwindigkeit: s₂ =  0,12 m/s · t₂

(s₁ + s₃) + s₂ = 0,12 m/s · t_1,3 + 0,12 m/s · t₂ = 0,2 m

0,12 m/s · (t_1,3 + t₂) = 0,2 m –>  (t_1,3 + t₂) = t_ges

t_ges = 0,2 m/s : 0,12 m = 

t_ges = 1,67 s