Werkstoffprüfung (1): Zugversuch 30.04.2012, 07:08
Mit Hilfe der Werkstoffprüfung ermittelt man wichtige Werkstoffkennwerte wie die Streckgrenze, die Bruchdehnung oder die Härte. Ein Schlüsselversuch ist dabei der Zugversuch. Mit Rechenaufgaben.
Zugversuch
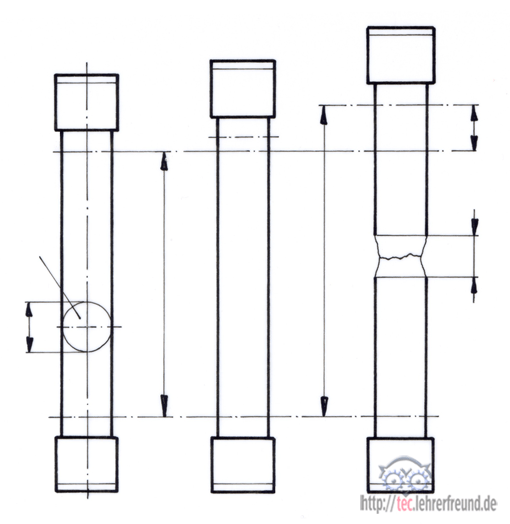
Beim Zugversuch werden Werkstoffe bis zum Bruch der genormten Zugproben gedehnt. Die Dehnung ΔLu (im Bild die rechte Zugprobe) ergibt sich aus einer zunehmenden Steigerung der Zugkraft F.
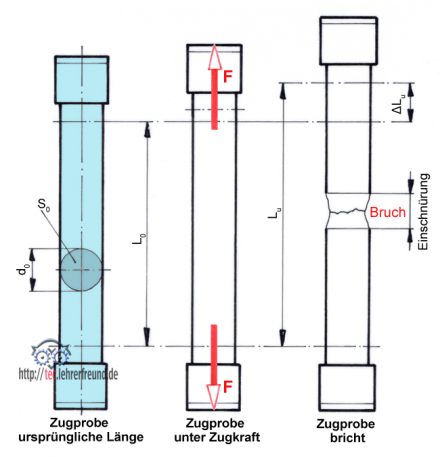
Für den Versuch und die darauf aufbauenden Festigkeitsberechnungen sind folgende Bezeichnungen wichtig:
Kräfte
F = Zugkraft, gemessen in N
Fm = Höchstkraft N
Fe = Zugkraft an der Streckgrenze N
Fp0,2 = Zugkraft an der Dehngrenze N
Abmessungen
d0 Anfangsdurchmesser der Probe, gemessen in mm
S0 Anfangsquerschnitt der Probe mm2
L0 Anfangsmesslänge mm
Lu Messlänge nach dem Bruch mm
ΔLu plastische Längenänderung mm
ΔLp0,2 Längenänderung an der Dehngrenze mm
ΔL Längenänderung mm
Spannungen
σ Zugspannung, gemessen in N/mm2
ε Dehnung %
Rm Zugfestigkeit N/mm2
Re Streckgrenze N/mm2
Rp0,2 Dehngrenze N/mm2
A Bruchdehnung %
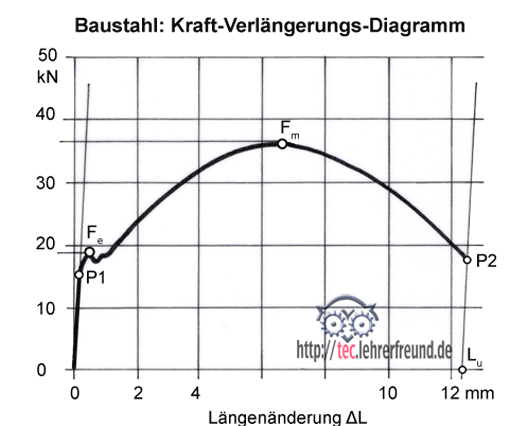
Kraft-Verlängerungs-Diagramm
Bei der Verlängerung der Zugprobe unterscheidet man einen elastischen und einen plastischen Bereich. Elastisch ist der Bereich, wenn die Verformung der Probe nach Entlastung vollständig zurück geht. Plastisch ist der Bereich, wenn die Verformung der Probe nach Entlastung nicht mehr vollständig zurück geht.
Die Verlängerungen werden in Abhängigkeit von der Zugkraft F im Kraft-Verlängerungs-Diagramm aufgezeichnet.
Zwischen der Geraden 0 - P1 und einer Parallelen dazu durch P2 liegt die plastische Verformung ΔLu (Bild oben).
Nach dem Bruch der Probe wird die Gesamtlänge Lu ermittelt. Sie enthält die plastischen Längenänderung ΔL = Lu - L0; diese Längenänderung entspricht der plastischen Verformung im Kraft-Verlängerungs-Diagramm.
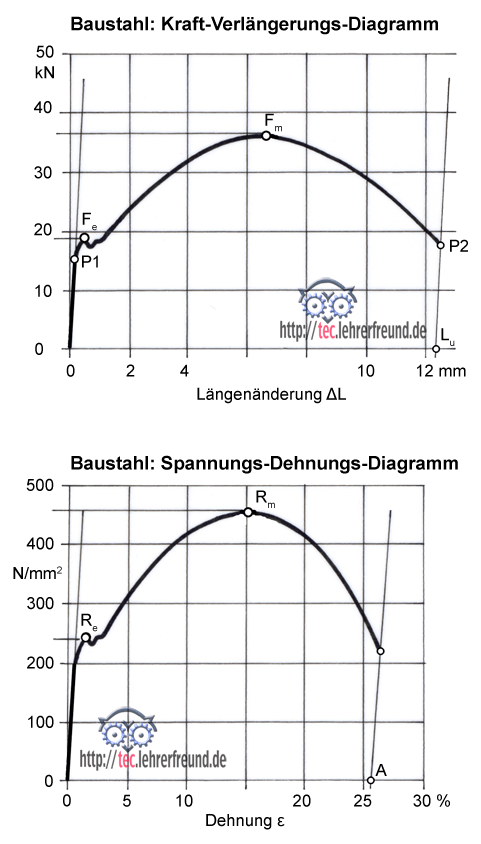
Im Zugversuch werden folgende Werkstoffkennwerte ermittelt:
Zugfestigkeit Rm
Sie ist die Zugspannung, die sich aus der Höchstkraft Fm und dem Anfangsquerschnitt S0 ergibt.
Rm = Fm : S0
Streckgrenze Re
Eine Streckgrenze beobachtet man nur bei Werkstoffen mit ausgeprägtem Fließbereich; sie wird aus der Kraft an der Streckgrenze Fe und dem Anfangsquerschnitt S0 als Zugspannung berechnet.
Re = Fe : S0
Dehngrenze Rp0,2
Sie gilt für Werkstoffe ohne ausgeprägten Fließbereich und wird aus der Kraft an der Dehngrenze Fp0,2 und dem Anfangsquerschnitt S0 als Zugspannung berechnet.
Rp0,2 = Fp0,2 : S0
Das Fließen: Bis zur Fließgrenze bleibt das Metall elastisch und nimmt wieder die ursprüngliche Form ein, wenn man die Belastung zurücknimmt. Wird die belastende Spannung im Material jedoch größer, dann beginnt es, zu »fließen«, d. h. sich bleibend zu verformen. Schließlich bricht es.
Bruchdehnung A
Die plastische Verlängerung ΔLu = Lu - L0 wird in Prozent (%) der Anfangsmesslänge L0 ausgedrückt. Bei gleichen Werkstoffen und gleichen Anfangsdurchmessern d0 der Proben führen größere Anfangsmesslängen L0 zu kleineren Werten der Bruchdehnungen A.
A = (Lu – L0) : L0 · 100%
Rechenbeispiel:
Eine Zugprobe aus Stahl S 275 JR wird im Zugversuch geprüft:
Anfangsdurchmesser d0 = 10 mm
Anfangsmesslänge L0 = 50 mm.
Im Verlauf des Prüfvorgangs wird das Kraft-Verlängerungs-Diagramm aufgezeichnet.
Ergebnisse:
Höchstkraft Fm = 35 814 N
Zugkraft an der Streckgrenze Fe = 18 100 N
Messlänge Lu nach dem Bruch der Probe 62,8 mm.
Zu berechnen sind
a) der Anfangsquerschnitt S0 der Probe
b) die Zugfestigkeit Rm
c) die Streckgrenze Re
d) die Bruchdehnung A
Lösungen (Berechnungsformeln oben benutzen):
a) der Anfangsquerschnitt S0 der Probe = 78,54 N/mm2
b) die Zugfestigkeit Rm = 456 N/mm2
c) die Streckgrenze Re = 230,5 N/mm2
d) die Bruchdehnung A = 25,6 %
Das Spannungs-Dehnungs-Diagramm
Das Kraft-Verlängerungs-Diagramm kann in ein Spannungs-Dehnungs-Diagramm (Bild oben) umgewandelt werden. Dazu rechnet man um
- die Kraftachse in die Spannungsachse und
- die Verlängerungsachse in die Dehnungsachse.
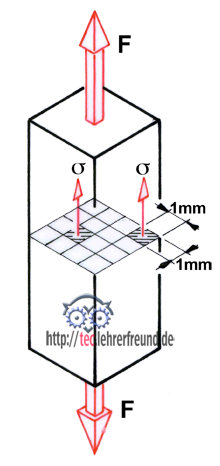
Spannung = Kraft pro Flächeneinheit,
Dehnung = Verlängerung in Prozent
Für jeden Kurvenpunkt des Diagramms gilt:
Zugspannung σ = F : S0 und
Dehnung ε = (ΔL : L0) • 100 %.
Danach entspricht die Kraft-Verlängerungs-Kurve dem Verlauf der Spannungs-Dehnungs-Kurve.
Beispiel: Im Zugversuch wird ein unlegierter Baustahl S 275 JR geprüft. Grundlage für die Lösung sind das Kraft-Verlängerungs-Diagramm, die Zugfestigkeit Rm = 456 N/mm2 und die Bruchdehnung A = 25,6 %. Nun wird das Kraft-Verlängerungs-Diagramm in das Spannungs-Dehnungs-Diagramm umgewandelt.
Lösungsvorschläge:
Im aufgezeichneten Diagramm müssen die Achsen neu eingeteilt und benannt werden. Kraft-Achse: Für die Zugkraft F = 35 814 N wird die Zugfestigkeit Rm = 456 N/mm2 eingetragen, die Achse neu eingeteilt und neu bezeichnet. Verlängerungsachse: Anstelle der Verlängerung ΔLu = 12,8 mm wird die Dehnung ε = 25,6 % mit verändertem Einteilungs-Maßstab eingetragen.
Dehngrenze Rp0,2
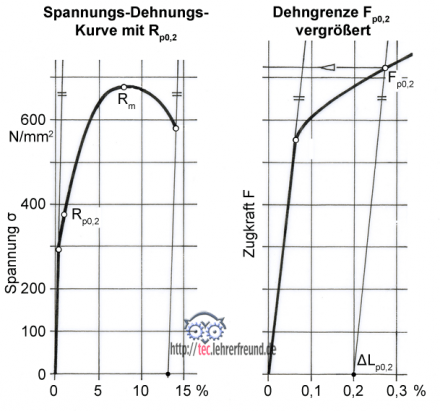
Bei Werkstoffen ohne ausgeprägte Streckgrenze Re - es sind meist härtere Stähle wie etwa Vergütungsstähle - setzt man als Ersatz für die Streckgrenze Re die Dehngrenze Rp0,2 ein. An der Dehngrenze Rp0,2 hat die Probe eine plastische Dehnung εp0,2 = 0,2 %.
In der Regel wird die Dehngrenze aus einem vergrößerten Ausschnitt des Kraft-Verlängerungs-Diagramms in vier Schritten ermittelt:
– Berechnung der Dehngrenzen-Längenänderung ΔLp0,2,
– Parallele zur Geraden O-P der Kraft-Verlängerungs-Kurve im Abstand ΔLp0,2 zeichnen,
– Dehngrenzenkraft Fp0,2 –> Schnittpunkt der Parallelen mit der Kraft-Verlängerungs-Kurve,
– Berechnung der Dehngrenze Rp0,2.
Übungsaufgabe:
Zugstäbe für Kranausleger aus Stahl S 275 JR werden im Zugversuch geprüft. Die Proben dafür haben einen Anfangsdurchmesser d0 = 8 mm und eine Anfangsmesslänge L0 = 40 mm.
Aus dem Kraft-Verlängerungs-Diagramm ergeben sich folgende Werte:
Höchstkraft Fm = 14,1 kN
Zugkraft an der Streckgrenze Fe = 9,2 kN
Messlänge Lu nach dem Bruch der Probe 49,2 mm.
Berechnen Sie
a) der Anfangsquerschnitt S0
b) die Zugfestigkeit Rm
c) die Streckgrenze Re
d) die Bruchdehnung A
Lösungen:
Anfangsquerschnitt S0 = 50,27 mm2
Zugfestigkeit Rm = 280,5 N/mm2
Streckgrenze Re = 183,0 N/mm2
Bruchdehnung A = 23 %
____________________
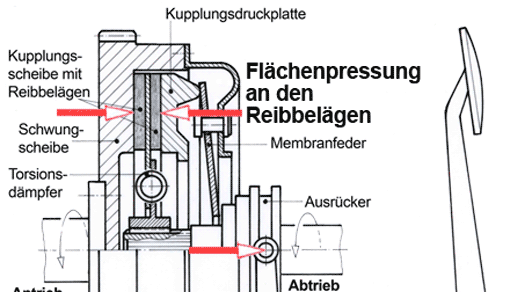
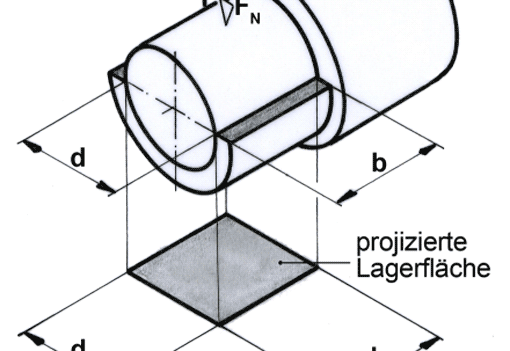
Dazugehörige Themen: Zugfestigkeit, Biegefestigkeit, Flächenpressung
____________________
Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.