Lagerkräfte berechnen 02.11.2008, 17:37
Eine der zahlreichen Anwendungsmöglichkeiten des Hebelgesetzes liegt in der Berechnung von Achs- und Lagerbelastungen.
2. Ausbildungsjahr
Lagerkräfte
Beim Berechnen von Hebeln geht man davon aus, dass der betrachtete Hebel im Gleichgewicht ist. Dies ist der Fall, wenn die Summe der linksdrehenden Momente gleich ist der Summe der rechtsdrehenden Momente (Mrechts = Mlinks).
Eine der vielen Anwendungsmöglichkeiten des Hebelgesetzes ist die Berechnung von Achs- und Lagerkräften.
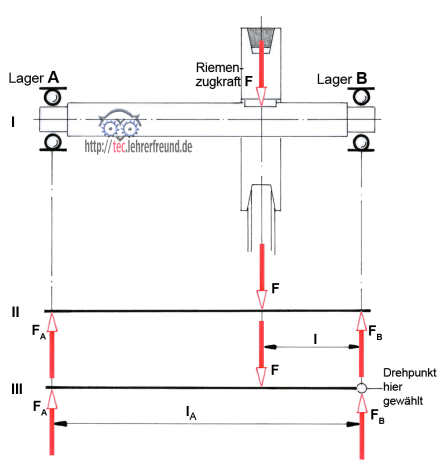
Beispiel, Skizze I: Am Riemenantrieb übt der Riemen auf die Scheibe, über die er läuft, eine Zugkraft F aus. Diese Kraft muss von den Wellenlagern A und B aufgenommen werden. Die uns interessierende Frage ist: Wie groß sind diese Lagerkräfte?
Nehmen wir an, der Riemenzug betrage F = 200 N. Wie stark werden die Lager belastet, wenn die Riemenscheibe
a) genau in der Mitte zwischen A und B sitzt,
b) nach rechts zum Lager B hin verschoben ist (wie in Skizze I)?
Im Fall a) erhält jedes Lager eine Druckkraft von 100 N; im Fall b) muss Lager B mehr als 100 N aufnehmen, Lager A weniger als 100 N. Zusammen ergeben beide Lagerkräfte 200 N.
Zu einer Formel, mit der wir dies genau berechnen können, kommen wir, wenn wir uns den Riementrieb unter einer Presse zu einem Hebel zusammengestaucht vorstellen (Skizze II). In diesen Hebel übernehmen wir zunächst nur die Kräfte von Skizze I. Die Lagerkräfte an den Stellen A und B bezeichnen wir mit FA und FB.
Skizze II stellt bis jetzt noch keinen Hebel dar, denn der Anordnung fehlt ein fast zu übersehender, aber deswegen nicht weniger wichtiger Bestandteil. Wissen Sie, welcher?
Sie haben es sicher herausgefunden: Damit wir das Ganze als Hebel bezeichnen können, muss ein Drehpunkt vorhanden sein. Bei Lagerberechnungen legen wir den Drehpunkt grundsätzlich in eines der beiden Lager, z. B. nach B (Skizze III). Der Sinn dieser Maßnahme: Wir schalten damit eine der beiden noch unbekannten Lagerkräfte als momentenwirksame Kraft aus. Das Drehmoment ist im Drehpunkt deswegen ausgeschaltet, weil es keinen Hebelarm besitzt: Kraft F mal Hebelarm Null = Null.
Jetzt komplettieren wir den Hebel, indem wir noch die Hebelarme eintragen: lA und l. Wir haben es nun mit einem einseitigen Hebel zu tun.
Aufgabe 1: Wir berechnen FA bei F = 200 N, lA = 210 mm und l = 65 mm.
Ansatz:
Mrechts = Mlinks
FA ⋅ lA = F ⋅ l usw.
(Lösung: FA = 61,9 N; FB wäre dann F – FA = 200 N – 61,9 N = 138,1 N).
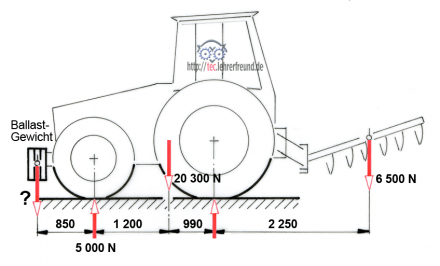
Was wir unter unserer »Gedankenpresse« zum Hebel zusammenquetschen, ist egal. Probieren wir es einmal mit einem Schlepper. Die Kraft F stellt in diesem Bild das Eigengewicht des Traktors dar, das wir uns in seinem Schwerpunkt vereinigt denken. Aus F entstehen die Achskräfte FA und FB.
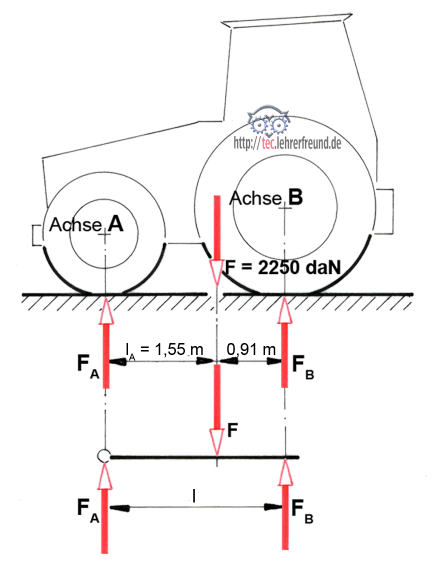
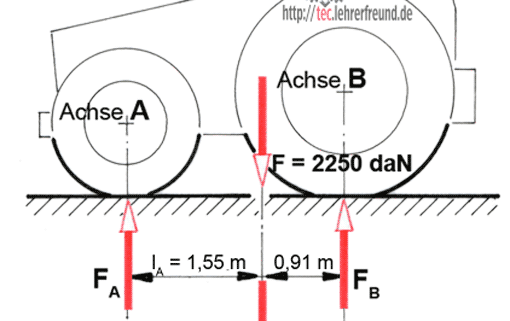
Berechnen Sie für den Schlepper zur Abwechslung FB zuerst. Dazu müssen Sie den Drehpunkt in die Achse A legen. (Vorsicht: Von den beiden eingetragenen Abständen taugt nur einer als Hebelarm. Der wirksame Hebelarm ist immer der (senkrechte) Abstand zwischen der Kraft und dem Drehpunkt).
(Lösung: Die Achskraft FB ist 1417,7 daN; FA = 2250 daN – 1417,7 daN = 832,3 daN).
Aufgabe 2: Wir erweitern unseren Schlepper aus Aufgabe 1 um ein Anbaugerät, z. B. einen Pflug. Wir wollen herausfinden, bei welchem Pfluggewicht F1 der Schlepper um die Hinterräder (Achse B) zu kippen beginnt. Überlegen Sie bitte zunächst, wie sich die Achsbelastungen FA und FB durch die zusätzliche Kraft F1 ändern.
Die Achse B wird durch den Pflug stärker belastet, FA wird kleiner. Wenn F1 immer größer würde, käme der Moment, in dem die vorderen Schlepperräder vom Boden abheben.
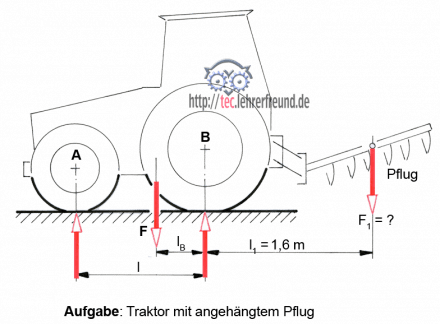
Der Rechnungsansatz beginnt wieder so:
Mrechts = Mlinks ->
F1⋅ l1 = F ⋅ lB usw. (FA ist beim Kippbeginn Null).
F1 = 1279,7 daN.
Was kann der Landwirt machen, wenn er ein Kippen befürchten muss? Er hängt am Traktor links vor dem Motor Ballastgewichte auf und erzeugt damit ein stabilisierendes linksdrehendes Moment.
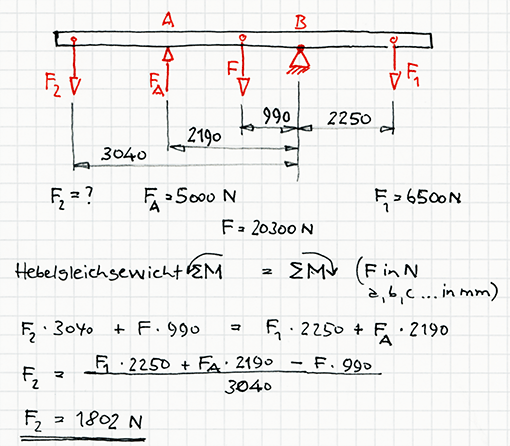
Hierzu eine weitere Aufgabe (Skizze unten): Wieviel Ballastgewicht muss aufgesetzt werden, wenn die Vorderreifen mit wenigstens 5 000 N auf den Boden drücken sollen? (Lösung: F Ballast = 1 802 N)
Eine Anmerkung: Sollte eine Lagerkräfte-Berechnung eine Kraft mit Minus-Vorzeichen ergeben, dann heißt dies: Die berechnete Kraft wirkt nicht wie (irrtümlich) angenommen, sondern in der entgegengesetzten Richtung.
Erläuterung für Timo (11. 6. 2016)